Informationen
Was ist ein Schallpegelmesser?
Inhaltsverzeichnis
3. Geräuschklassifizierung
3.1 Lärmklassifizierung basierend auf zeitlichen Schwankungen der Pegel
3.2 Geräuschklassifizierung anhand von Frequenzspektren
4. Einheit der Geräuschmessung – Warum die logarithmische Skala „dB“ verwendet wird
5. Physikalische Schallmaße
5.1 Schalldruckpegel
5.2 Schallintensitätspegel
5.3 Schallleistungspegel
5.4 Oktavbandpegel, 1/3 Oktavbandpegel
6. Sensorische Schallmaße
6.1 Lautstärke
6.2 Spielfeld
6.3 Klangfarbe
6.4 Lautstärkepegel
6.5 A-bewerteter Schalldruckpegel
7. Übersicht Schallpegelmesser
7.1 Was ist ein Schallpegelmesser?
7.2 Unterschiede zwischen Schallpegelmessern (Klasse 2) und Präzisionsschallpegelmessern (Klasse 1)
7.3 Kalibrierung
7.4 Messbereiche von Schallpegelmessern (Linearitätsbereiche)
7.5 Windschutz
7.5.1 Warum ist ein Windschutz notwendig?
7.5.2 Leistung von Allzweck-Windschutzscheiben
7.5.3 Allwetter-Windschutz
8. Struktur des Schallpegelmessers
8.1 Blockdiagramm
8.2 Mikrofon und Vorverstärker
8.3 Frequenzbewertung Z- (oder FLAT-), A- und C- Bewertung
8.4 Schnelle und langsame Zeitbewertung
8.5 AC-Ausgang und DC-Ausgang
8.5.1 AC-Ausgang
8.5.2 DC-Ausgang
8.6 Anzeige
9. Ablesung des Schallpegelmessers
9.1 Schalldruckpegel (Lp)
9.2 A-bewerteter Schalldruckpegel (LA)
9.3 Äquivalenter kontinuierlicher A-bewerteter Schalldruckpegel (LAeq, T)
9.4 Schallbelastungspegel (LAE)
9.5 Perzentil Schalldruckpegel (Lx)
9.6 Maximaler Geräuschpegel (Lmax) und minimaler Geräuschpegel (Lmin)
9.7 Maximalwert (Tactmax) über N Sekunden
9.8 Spitzenpegelwert (Lpeak)
10. Verfahren zur Messung des äquivalenten kontinuierlichen A-bewerteten Schalldruckpegels (Übersicht über JIS Z8731:1999)
10.1 Äquivalenter kontinuierlicher A-bewerteter Schalldruckpegel
10.2 Begriffsdefinitionen
10.3 Arten von Geräuschen
10.4 Schallpegelmesser und Kalibrierung
10.5 Messpunkt
10.6 Methoden zur Lärmmessung
10.7 Informationen, die aufgezeichnet werden sollten
10.8 Anhang 1 (Regeln): Erhebung akustischer Daten für eine angemessene Flächennutzung
10.9 Anhang 2 (Referenzmaterial): Ergänzende Hinweise zur Beschreibung und Messverfahren für Umgebungslärm
10.10 Umgebungsbedingungen, die die Messung beeinflussen können
10.11 Schallausbreitung und -dämpfung mit der Entfernung
11. Oktavbandanalyse (Frequenzanalyse)
11.1 Oktavbandanalyse
11.2 JIS-Standards für Oktavfilter
11.3 Oktaven Filterbandbreite und Mittenfrequenz
11.4 Berechnung des Gesamtpegels (Gesamtbandpegel)
11.5 ALLPASS und GESAMT
11.6 NC (Lärmkriterien)
11.7 Lautheitsanalyse (Loudness, Loudness Level, Sharpness)
12. Berechnung von Dezi Bel (dB)
12.1 Summe der dB-Werte (Gesamtleistung)
12.2 Durchschnitt der dB-Werte (Durchschnittsleistung)
12.3 Differenz der dB-Werte (Leistungsdifferenz)
12.4 Logarithmische Gleichung
12.5 Methode zur Berechnung des äquivalenten kontinuierlichen A-bewerteten Schalldruckpegels
12.6 Methode zur Messung des Perzentil-Schalldruckpegels (50 Messungen)
1. Was ist Ton?
Unter Schall versteht man allgemein Wellen (akustische Wellen, elastische Wellen), die sich durch Medien wie Gase, Flüssigkeiten und Festkörper ausbreiten. Dieser Leitfaden befasst sich hauptsächlich mit akustischen Wellen, die sich durch Luft ausbreiten. Schallwellen, die sich mit etwa 340 m/s ausbreiten, sind ein Wellenphänomen. Wir hören diese Wellen, wenn sie durch die Luft wandern. Diese Wellen werden erzeugt, wenn der atmosphärische Druck der Luft ständig schwankt (dh wechselnde Druckschwankung). Eine Druckschwankung abseits des atmosphärischen Drucks (statischer Druck) wird allgemein als Schalldruck bezeichnet. Das Folgende sind Zitate aus IEC 60050-801 (JIS Z 8106:2000).
Momentaner Schalldruck
Der Wert, der durch Subtraktion des statischen Drucks vom Druck an einem Punkt des Mediums zu einem bestimmten Zeitpunkt erhalten wird.
Schalldruck
Der quadratische Mittelwert des momentanen Schalldrucks über einen bestimmten Zeitraum, sofern nicht anders angegeben.

Abbildung 1.1: Fluss der grundlegenden Verarbeitung durch einen Schallpegelmesser
Wie oben gezeigt, unterscheidet der IEC (JIS)-Standard eindeutig den momentanen Schalldruck vom Schalldruck (siehe Abbildung 1.1).
Beachten Sie, dass in diesem Handbuch; Der Begriff "Schalldruck" bezieht sich entweder auf den "Schalldruck" oder den "momentanen Schalldruck", wie in IEC 60050-801 (JIS Z 8106:2000) definiert, je nachdem, was zutreffend ist.
Eine Person mit normalem Gehör kann einen Schalldruckbereich von 20 μPa bis 20 Pa hören. Das Symbol μ, was Mikro bedeutet, wird verwendet, um 10 -6 darzustellen . Das bedeutet, dass das lauteste hörbare Geräusch 10 6 mal lauter ist als das kleinste hörbare Geräusch. Pa ist eine Druckeinheit. 1 Pa entspricht dem Druck, der entsteht, wenn 1 N (mit einem Gewicht von etwa 0,1 kg) auf eine Fläche von 1 m 2 ausgeübt wird . Der in Wettervorhersagen verwendete Luftdruck wird in hPa ausgedrückt, was 100-mal größer als 1 Pa ist. (1 atm entspricht etwa 1013 hPa.)
Wie bei der Schallintensität kann ein normalhörender Jugendlicher den momentanen Schalldruck in einem Frequenzbereich von etwa 20 Hz bis zu dem etwa 1000-fach höheren 20 kHz hören. Schall kann grob in die folgenden Frequenzbänder eingeteilt werden.
Unter 20 Hz: Infraschall
20 Hz bis 20 kHz: Hörbarer Schall
Über 20 kHz: Ultraschall
Wir unterscheiden verschiedene Klänge anhand der folgenden Klangeigenschaften.
Tonhöhe
Die Tonhöhe ist der Grad der Höhe oder Tiefe eines Tons, der durch die Frequenz des Tons bestimmt wird. Je höher die Frequenz, desto höher der Ton. Je niedriger die Frequenz, desto tiefer der Ton.
Lautstärke
Es gibt ein lauteres "a" und ein weniger lautes "a", beide mit der gleichen Tonhöhe. Sie haben ähnliche Wellenformen, aber ein lauteres „a“ hat eine große Amplitude und ein weniger lautes „a“ hat eine kleinere Amplitude. Schallpegelmesser dienen zur Messung der Lautstärke von Schall.
Klangfarbe/ Ton
Wir können verschiedene Musikinstrumente unterscheiden, selbst wenn sie Töne mit der gleichen Tonhöhe und Lautstärke abgeben. Dies liegt daran, dass wir in der Lage sind, verschiedene Arten von Klangfarben und Tönen zu unterscheiden. Obwohl weder Klangfarbe noch Ton vollständig geklärt sind, wird davon ausgegangen, dass sie mit der Wellenform des Klangs zusammenhängen.
Als Wellen hat Schall auch verwandte Effekte wie Reflexion, Übertragung und Beugung, die unten gezeigt werden, die proportional zur Entfernung gedämpft werden.

Abbildung 1.2: Klangeffekte
2. Was ist Lärm
Unter verschiedenen Arten von Geräuschen bezieht sich Lärm kollektiv auf unangenehme und störende Geräusche, die niemand hören möchte. Die weiter oben in diesem Leitfaden erwähnte IEC 60050-801 (JIS Z 8106:2000) definiert Lärm als unangenehme oder unerwünschte Geräusche oder andere Störungen. Unangenehme Geräusche können die Gesundheit und das Wohnumfeld schädigen und sich zur Lärmbelästigung entwickeln.
Aus dem hörbaren Schallbereich von 20 Hz bis 20 kHz behandelt die Geräuschbewertung speziell den Bereich von etwa 50 Hz bis 5 kHz. In alltäglichen Gesprächen ist der Bereich von 300 Hz bis 3 kHz wichtig, um hörbar zu sein. Überstunden in lautem Lärm zu arbeiten, kann Ihr Gehör schädigen. Lärmschutzvorschriften sollen uns vor Lärm schützen und zu einem normalen Leben beitragen.
Schallpegelmesser werden normalerweise zur Messung und Beurteilung von Lärm verwendet. Es gibt zwei Arten von Geräuschmessungen: physisch und sensorisch. Physikalische Schallmaße umfassen Schalldruckpegel, Schallintensitätspegel, Schallleistungspegel sowie Oktav- und 1/3-Oktavbänder für die Frequenzanalyse. Sensorische Schallmaße umfassen Lautstärke, Tonhöhe, Klangfarbe, Lautstärkepegel und A-bewerteter Schalldruckpegel. Viele dieser Maßnahmen wurden von JIS (Japanese Industrial Standard) und der IEC (International Electrotechnical Commission) definiert. Sensorische Messungen sind ein wachsendes Wissenschaftsgebiet mit zahlreichen Studien, die in der Vergangenheit durchgeführt wurden und noch durchgeführt werden müssen.
Für unterschiedliche Bewertungszwecke werden unterschiedliche Schallmaße verwendet: A-bewerteter Schalldruckpegel zur Bewertung von Umgebungslärm; Schallleistungspegel und 1/3-Oktavband für die Produktentwicklung; und in jüngerer Zeit Tonqualitätsbewertungsparameter. Weitere Einzelheiten finden Sie in den Kapiteln 5, 6 und 11.
Schallpegelmesser wurden zum Messen des Schalldruckpegels und des A-bewerteten Schalldruckpegels verwendet. Mit technologischen Fortschritten in den letzten Jahren gibt es heute einige Modelle im Handel, die auch Oktavband- und 1/3-Oktavband-Pegel und -Lautstärke messen können.
Schauen wir uns das Rauschen genauer an.

Abbildung 2.1: Typische Geräusche und ihre Pegel
3. Geräuschklassifizierung
Rauschänderungen können grob in Pegelschwankung auf der Zeitachse und spektrale Komponentenunterschiede auf der Frequenzachse unterteilt und Rauschen entsprechend klassifiziert werden.
Hinweis:
Dieses Kapitel basiert auf Zitaten aus JIS Z 8733:2000 Anhang F „Klassifizierung von Geräuschen basierend auf Spektren und zeitlichen Schwankungen von Pegeln“ (ISO 12001).
3.1 Klassifizierung von Lärm basierend auf zeitlichen Schwankungen der Pegel

Diese Arten von Rauschen haben die folgenden Eigenschaften und typischen Zeitachsen-Wellenformen.
Stetiges Rauschen
Konstantes Rauschen ist ein Rauschen, das am Messpunkt ungefähr auf dem gleichen Pegel bleibt, ohne oder mit geringfügigen Schwankungen des Zählerstands.

Abbildung 3.1
Schwankendes Rauschen
Schwankendes Rauschen ist ein Rauschen, dessen Pegel am Messort ziemlich breit und unregelmäßig schwankt. Ein typisches Beispiel ist Lärm, der in der Nähe einer Straße mit einem bestimmten Fahrzeugverkehr gemessen wird.

Abbildung 3.2
Intermittierendes Rauschen
Intermittierendes Rauschen ist ein Rauschen, das in Zeitintervallen auftritt, wobei jede Rauschperiode länger als mehrere Sekunden dauert. Einige Zeitintervalle sind ziemlich regelmäßig, während andere Zeitintervalle unregelmäßig sind, beispielsweise wenn Züge und Flugzeuge vorbeifahren.

Abbildung 3.3
Ein isolierter Ausbruch von Schallenergie
Impulsschall, der getrennt werden kann, ist ein isolierter Ausbruch von Schallenergie, ein typisches Beispiel dafür ist ein Stapelhammer. Einige sind ein einzelner Burst, während andere intermittierend auftreten. Einige bleiben ungefähr auf dem gleichen Niveau, während andere ziemlich stark schwanken. Was normalerweise als isolierte Ausbrüche von Schallenergie bezeichnet wird, tritt in Intervallen von 0,2 Sekunden oder mehr auf.

Abbildung 3.4
Quasi-stetes impulsives Rauschen
Quasi-stetige impulsive Geräusche treten in extrem kurzen Intervallen (ungefähr weniger als 0,2 Sekunden) auf, während sie ungefähr auf dem gleichen Pegel bleiben, Beispiele dafür sind Glocken und Gesteinsbohrmaschinen. Es gibt viele Fälle, in denen quasi-stetiges Impulsrauschen als stetiges Rauschen wahrgenommen wird.

Abbildung 3.5
3.2 Geräuschklassifizierung anhand von Frequenzspektren
Rauschen kann basierend auf der Spektralform auf der Frequenzachse in die folgenden drei Typen eingeteilt werden.

Diese Arten von Rauschen haben die folgenden Eigenschaften und typischen spektralen Wellenformen.
Breitbandrauschen
Breitbandrauschen hat eine spektrale Form mit Schallenergie, die über einen relativ breiten Frequenzbereich verteilt ist.
Beispiele: Geräusch eines Sturzes, Geräusche von Lüftungsschlitzen von Klimaanlagen, Straßenlärm usw.

Abbildung 3.6
Schmalbandiges Rauschen
Schmalbandrauschen hat eine spektrale Form mit Schallenergie, die in einem relativ schmalen Frequenzbereich (innerhalb des 1/3-Oktavbandes) konzentriert ist, und hat keinen diskreten Ton.
Beispiele: Donner in der Ferne (niedrige Frequenz), Windgeräusche, die über eine Wiese oder eine Schlucht wehen (mittlere Frequenzen), Luftgeräusche, die aus einem Fahrzeugreifen entweichen (hohe Frequenzen) usw.

Abbildung 3.7
Diskreter Ton
Diskreter Ton hat periodische Schalldruckschwankungen mit einem Gefühl von Tonhöhen- und Linienspektralfrequenzen.
Beispiele: Summen eines Ventilators, Piepen von einem digitalen Gerät, Ton eines Musikinstruments usw.

Abbildung 3.8
4. Einheit der Geräuschmessung – Warum die logarithmische Skala „dB“ verwendet wird
Logarithmische Skala „dB“
In Kapitel 1 haben wir gelernt, dass Menschen Schall (hörbaren Schall) in einem Frequenzbereich von etwa 20 Hz bis 20 kHz und einem Schalldruckbereich von 20 μPa bis 20 Pa hören können und dass der lauteste Schall 10 6 mal lauter ist als der leiseste Lauter Ton. Normalerweise werden logarithmische Skalen verwendet, um Größen mit einem breiten Dynamikbereich effizient darzustellen. Dies gilt auch für Schalldruck und Lärm, da diese in weiten Bereichen schwanken können. Das Weber-Fechner-Gesetz besagt, dass die Größe einer subjektiven Empfindung proportional zum Logarithmus der Reizintensität zunimmt. Der Hörsinn ist eine subjektive Empfindung, weshalb logarithmische Skalen verwendet werden, um Schall darzustellen.
Bel wird als Einheit von logarithmischen Skalen verwendet. Dies liegt daran, dass Alexander Graham Bell aus den USA die Einheit erstmals verwendet hat, um die Dämpfung der Energieübertragung bei Telefongesprächen darzustellen. Da Bel für diesen Zweck zu groß ist, wird in der Praxis als logarithmische Skaleneinheit Dezi Bel (dB) verwendet, was einem Zehntel von Bel entspricht. 1 B ist gleich 10 dB.
Hinweis:
- Das Dezi (d) ist ein Präfix und bedeutet 10 -1 für SI-Einheiten (SI = The International System of Units).
- B (Bel) darf als Einheit für den A-bewerteten Schallleistungspegel verwendet werden, um ihn klar von dB für den abgestrahlten Schalldruckpegel zu unterscheiden. (ISO 9296 1988, JIS X 7778:2001 Deklarierte Geräuschemissionswerte von Computer- und Bürogeräten)
Die Einheit Dezi Bel (dB) wird häufig in der Elektro- und Kommunikationsbranche verwendet, weil sich neben den oben beschriebenen Gründen die Verstärkung von mehrstufig geschalteten Verstärkern, Dämpfungsgliedern und anderen Geräten mit der Einheit einfach durch Addition und Subtraktion berechnen lässt. Wie oben erwähnt, wird Dezi Bel (dB) als Einheit für die Dämpfung (Rate) der Leistungsübertragung verwendet. Es ist definiert als:

Gleichung 4.1
Wobei E die gemessene Leistung und E 0 die Referenzleistung ist.
Wie Gleichung 4-1 zeigt, ist Dezi Bel (dB) ein relativer Wert, definiert als dezimaler Logarithmus eines Leistungsverhältnisses. Er kann als Absolutwert behandelt werden, wenn der Bezugswert (z. B. E 0 ) eindeutig definiert ist. Bei der Verwendung von Dezi Bel ist es wichtig, den Referenzwert zu klären und zu beachten.
In der Welt des Schalls ist das Quadrat des Schalldrucks proportional zur Schallintensität. Basierend auf diesem Prinzip kann der Schalldruckpegel L P (dB), eine der von Schallpegelmessern verwendeten Einheiten, ausgedrückt werden durch

Gleichung 4.2
Der A-bewertete Schalldruckpegel L A (dB) kann durch die folgende Gleichung unter Verwendung des A-bewerteten Schalldrucks p A ausgedrückt werden . (Weitere Informationen finden Sie in Abschnitt 8.3, „Frequenzkorrekturschaltung“.)

Gleichung 4.3
In der Welt des Schalls (Vibration) wird der Begriff „Schall(druck)pegel“ (dB) verwendet, um die Lautstärke (Intensität) von Schall auszudrücken. Außerdem ist, wie oben gezeigt, der absolute Referenzschalldruck für dB eindeutig als p 0 (20 μPa) definiert. Beispielsweise wird der quadratische Mittelwert des Schalldrucks für beispielsweise 100 dB zu 2 Pa bestimmt. Berechnungsmethoden mit dezi Bel werden später in diesem Handbuch erläutert.
Hinweis: dB SPL
Früher wurde für den Schalldruckpegel (SPL) die Einheit „dB SPL“ verwendet. Heutzutage wird der Schalldruckpegel nur in „dB“ ausgedrückt, einschließlich JIS und Gesetzen wie dem Messgesetz.
5. Physikalische Schallmaße
5.1 Schalldruckpegel
Der Schalldruckpegel L p (dB) kann ausgedrückt werden als:

Gleichung 5.1
wobei p (Pa) der Effektivwert des momentanen Schalldrucks eines gegebenen Schalls und p 0 (Pa) der Bezugsschalldruck ist.
Der Referenzschalldruck p 0 in atmosphärischer Umgebung beträgt 20 μPa, was ungefähr dem minimal hörbaren Wert für einen reinen Ton bei 1 kHz für normalhörende Personen entspricht. Abbildung 5-1 zeigt den Zusammenhang zwischen Schalldruck p (Pa) und Schalldruckpegel L p (dB). Ein Schalldruck von 20 μPa entspricht einem Schalldruckpegel von 0 dB. Schalldruck von 1 Pa entspricht Schalldruckpegel von 94 dB. Ein Schalldruck von 20 Pa entspricht einem Schalldruckpegel von 120 dB. Bei einer Änderung von 0,1 atm (ca. 100 hPa = 10 4 Pa) beträgt der Schalldruckpegel 174 dB.

Abbildung 5.1: Zusammenhang zwischen Schalldruck p und Schalldruckpegel L p
5.2 Schallintensitätspegel
Die Energie I (W/m 2 ) des Schalls, der pro Zeiteinheit senkrecht zur Richtung der Schallwellen durch eine Flächeneinheit geht, kann ausgedrückt werden durch.

Gleichung 5.2
wobei der quadratische Mittelwert des Schalldrucks, der sich durch den Raum ausbreitet, p (Pa) ist und die Geschwindigkeit von mittleren Partikeln, die durch Schallwellen in Schwingung versetzt werden, u (m/s) ist.
Diese Größe wird „Schallintensität“ I (W/m 2 ) genannt.
Bei ebenen Schallwellen (deren Oberfläche eben und senkrecht zur Ausbreitungsrichtung ist) gilt:

Gleichung 5.3
wobei die Volumendichte des Mediums ρ (kg/m 3 ) und die Schallgeschwindigkeit im Medium c (m/s) ist.

Gleichung 5.4
Wenn die obige Gleichung in Gleichung 5-2 eingesetzt wird, kann die Schallintensität I wie folgt ausgedrückt werden: Betrachten wir das folgende Beispiel. Bei 20 °C beträgt die Volumendichte der Luft ρ 0 1,205 kg/m 3 und die Schallgeschwindigkeit c 0 343 m/s. Unter diesen Bedingungen lässt sich bei sich in Luft ausbreitenden ebenen Wellen die dem Bezugsschalldruck p 0 = 2×10 -5 Pa entsprechende Schallintensität I wie folgt ausdrücken:

Gleichung 5.5
Dieser Wert, der fast gleich 10 –12 W/m 2 ist, wurde aufgrund einer internationalen Vereinbarung als Bezugsschallintensität I0 verwendet, die dem Bezugsschalldruck p 0 entspricht . Analog zum Schalldruckpegel lässt sich der Schallintensitätspegel L I (dB) anhand der Bezugsschallintensität I 0 wie folgt definieren :

Gleichung 5.6
Während die Referenzschallintensität I 0 für ebene Schallwellen erhalten wurde, kann die Gleichung 5-6 für den Schallintensitätspegel auch für gewöhnliche Schallwellen verwendet werden. Bei ebenen Schallwellen, bei denen Gleichung 5-4 gilt, wird der Schallintensitätspegel bei 20 °C wie folgt berechnet:

Gleichung 5.7
Dies entspricht fast dem Schalldruckpegel. Da aber die Volumendichte der Luft ebenso wie die Schallgeschwindigkeit temperaturabhängig ist, ergibt sich bei Temperaturen außerhalb von 20 °C eine Differenz zwischen Schalldruckpegel und Schallintensitätspegel von etwa 0,2 bis 0,3 dB. An einem Punkt in der Nähe einer Schallquelle und an anderen bestimmten Punkten werden Schallwellen nicht als ebene Wellen angesehen, wodurch es ungültig wird, den Schallintensitätspegel einfach auf der Grundlage des Schalldruckpegels zu berechnen.
5.3 Schallleistungspegel
Schallwellen, die sich in einem Medium ausbreiten, können als Energiefluss betrachtet werden. Diese Energie wird Schallenergie genannt. Schallenergie, die pro Zeiteinheit eine Flächeneinheit durchdringt, kann als Schallenergiemenge angesehen werden und wird als Schallleistung P (W) bezeichnet.
Bei ebenen Schallwellen kann die Schallleistung P , die durch eine Ebene senkrecht zur Schallausbreitungsrichtung tritt, wie folgt berechnet werden:

Gleichung 5.8
Dabei ist p (Pa) der mittlere quadratische Schalldruck, ρ (kg/m 3 ) die Volumendichte des Mediums, c (m/s) die Schallgeschwindigkeit und S (m 2 ) die Fläche der Ebene.
Die als Pegel relativ zu einem Bezugswert P 0 ausgedrückte Größe der Schallleistung P wird als Schallleistungspegel L W (dB) bezeichnet und kann wie folgt definiert werden:

Gleichung 5.9
Der Referenz-Schallleistungspegel P 0 beträgt 10 –12 W, was dem Referenzwert I 0 (10 –12 W/m 2 ) beim Schallintensitätspegel L I multipliziert mit einer Flächeneinheit entspricht. Schallleistung wird hauptsächlich verwendet, um die Intensität der Schallenergie auszudrücken, die von einer Schallquelle abgestrahlt wird. Die Gesamtschallenergie, die von einer Schallquelle pro Zeiteinheit innerhalb eines bestimmten Frequenzbereichs abgestrahlt wird, wird als Schallleistung (Schallleistung einer Schallquelle) P (W) bezeichnet, und der Pegel der Schallleistung wird als Schallleistungspegel (Schallleistungspegel) bezeichnet einer Schallquelle) L W (dB).
5.4 Oktavbandpegel, 1/3 Oktavbandpegel
Um die physikalischen Eigenschaften eines Schalls zu verstehen, reicht es nicht aus, seinen Gesamtschalldruck und seine Intensität zu klären. Es ist auch notwendig, den Schalldruck und die Intensitätspegel bei jeder Frequenz zu klären (dh Frequenzanalyse). Filter mit konstantem Verhältnis, wie beispielsweise Oktavbandfilter und 1/3-Oktavbandfilter, werden üblicherweise für die Frequenzanalyse von Schall verwendet. Diese Analysatoren wurden dank aktiver Filterung für integrierte Schaltungen und andere elektronische Schaltungstechnologien in Größe und Preis reduziert, was dazu beiträgt, die Messgenauigkeit und Benutzerfreundlichkeit zu verbessern. Oktavbandfilter werden in Kapitel 11 ausführlich erklärt.
6. Sensorische Schallmaße
6.1 Lautstärke
Die Schalllautstärke ist eine sensorische Größe, die sich auf die Schallintensität bezieht, und ist eine der grundlegendsten Eigenschaften des Hörsinns, zu der auch Tonhöhe und Klangfarbe gehören. Die Maßeinheit für die Lautstärke ist Sone, wobei 1 Sone einem reinen Ton (1 kHz) mit einem Schalldruckpegel von 40 dB entspricht. Ein Ton, den eine Person mit normalem Gehör für doppelt so laut wie 1 Sone hält, wird mit 2 Sone bewertet.
Abbildung 6.1 zeigt die Beziehung zwischen Schalldruckpegel (dB) und Lautstärke (Sone) für jedes Oktavband. Bei 1 kHz verdoppelt eine Erhöhung des Schalldrucks um 10 dB die Lautstärke um 1 Sone. Dies gilt auch für andere Frequenzbänder, wobei eine Erhöhung um 10 dB die Lautstärke nicht gerade verdoppelt. Dies zeigt, dass die Lautstärke weitgehend eine Funktion der Schallintensität und -frequenz ist. Die Lautstärke ist auch eine Funktion der Tondauer, wobei Menschen einen Ton als gleichmäßig wahrnehmen, wenn er 150 bis 300 ms dauert.

Abbildung 6.1: Zusammenhang zwischen Schalldruckpegel und Lautstärke
6.2 Spielfeld
Wie weiter oben in diesem Handbuch beschrieben, ist die Tonhöhe ein sensorisches Konzept, das sich auf die Tonfrequenz bezieht. Bei einem reinen Ton mit konstanter Intensität ist die Tonhöhe proportional zur Frequenz: Je höher die Frequenz, desto höher die Tonhöhe. Die Maßeinheit für die Tonhöhe ist Mel, wobei 1000 Mel einem reinen Ton mit einer Frequenz von 1 kHz und einem Schalldruckpegel von 40 dB entsprechen.
Auch hier wird die Tonhöhe weitgehend durch die Frequenz des Tons bestimmt. Die Tonhöhe des zusammengesetzten Klangs ist jedoch nicht so einfach und wird von der Zusammensetzung der Frequenzen und anderen Faktoren beeinflusst. Es wird auch von der Schallintensität beeinflusst und davon, ob es vorhergehende und/oder nachfolgende Geräusche gibt.
6.3 Klangfarbe
Wir können verschiedene Musikinstrumente unterscheiden, selbst wenn sie Töne mit der gleichen Lautstärke und Tonhöhe abgeben, weil sich ihre Töne unterschiedlich anfühlen. Diese Unterschiede ergeben sich aus den spezifischen Eigenschaften ihrer Klangfarbe.
Obwohl es seit Jahren untersucht wird, ist die Klangfarbe nicht vollständig verstanden. Laut neueren Studien wird die Klangfarbe von drei Faktoren bestimmt, nämlich ästhetischen, metallischen und kraftvollen Faktoren.
6.4 Lautstärkepegel
Die Lautstärke wird maßgeblich durch die Intensität des Schalls bestimmt. Es hängt auch von der Frequenz und Dauer des Tons ab, wobei Menschen einen Ton als konstant wahrnehmen, wenn er 150 bis 300 ms dauert.
Auf der Grundlage des oben Gesagten wird der Schalldruckpegel eines reinen Tons von 1 kHz, den Menschen mit normalem Gehör als mit der gleichen Lautstärke wie der fragliche Dauerton bestimmen, als der Lautstärkepegel des Tons P (Phon) definiert.
Die Messung frequenzbedingter Veränderungen der menschlichen Hörempfindung wurde erstmals von Fletcher-Munson durchgeführt und 1957 erneut von Robinson, F. et al. untersucht. Abbildung 6-2 zeigt die Beziehung zwischen den Schalldruckpegeln von reinen Tönen, die Menschen mit normalem Gehör als mit der gleichen Lautstärke und den gleichen Frequenzen wahrnehmen, gemessen von Robinson et al. Diese Kurven werden Kurven gleicher Lautstärke oder Konturen gleicher Lautstärke genannt. Später wurde festgestellt, dass die von Robinson, F. et al. erhebliche Fehler enthalten. Im Jahr 2003 wurden neue Konturen mit gleichem Lautstärkepegel als ISO 226 eingeführt. In Abbildung 6-2 sind die alten Konturen mit gleichem Lautstärkepegel in Blau und die neuen Konturen in Rot dargestellt.

Abbildung 6.2: Alte und neue Konturen mit gleichem Lautstärkepegel
Abbildung 6.2 zeigt, dass der menschliche Gehörsinn die folgenden Eigenschaften hat.
- Die Empfindlichkeit der Ohren sinkt im Tieftonbereich deutlich ab. Schauen wir uns die Kontur für 40 Phon an. Für einen reinen Ton von 40 dB, 1 kHz erfordert die gleiche Lautstärke etwa 10 dB mehr bei 250 Hz und etwa 35 dB mehr bei 63 Hz.
- Die Ohren sind bei etwa 4 kHz am empfindlichsten, einige dB empfindlicher als bei 1 kHz.
- Im Frequenzbereich über 4 kHz ist die Empfindlichkeit der Ohren zu höheren Frequenzen hin weniger empfindlich.
- Die für Menschen hörbaren Frequenzen reichen je nach Schallintensität von 15 bis 20 Hz bis etwa 20 kHz.
Die Konturen gleicher Lautstärkepegel können als Durchschnittswerte für viele junge Menschen interpretiert werden, obwohl es große individuelle Unterschiede gibt. Ab dem 20. Lebensjahr setzt die Alterung ein und danach sinkt die obere hörbare Frequenzgrenze weiter.
Auch hier kann die Lautstärke eines reinen Tons unter Verwendung von Konturen mit gleichem Lautstärkepegel bestimmt werden. Bei zusammengesetzten Geräuschen wurden eine Reihe von Methoden zur Vorhersage des Lautstärkepegels basierend auf dem Schalldruck vorgeschlagen, wie z. B. 1937 von Fletcher-Munson. Die von Stevens, S. und Zwicker, E. entwickelten Methoden wurden als ISO 532 übernommen.
6.5 A-bewerteter Schalldruckpegel
Lärm ist für den Menschen ein unerwünschter Schall. Als Lärm wird jedes Geräusch bezeichnet, das von den Hörern als unangenehm oder störend empfunden wird. Lärm ist eine sensorische Größe, die auf dem menschlichen Hörsinn basiert, und muss daher mit einer Einheit gemessen werden, die auf dem Hörsinn und nicht auf der physischen Lautstärke basiert. Aus diesem Grund wird als Maßeinheit (dB) für den Schallpegel L A der A-bewertete Schalldruckpegel auf Basis der in Abschnitt 6-4 erläuterten Konturen gleicher Lautstärkepegel verwendet .
A-bewertete Schalldruckpegel werden mit Schallpegelmessern gemessen. Ein Schallpegelmesser verwendet ein Mikrofon (normalerweise ein Kondensatortyp), um elektrische Signale zu erzeugen, die proportional zum Schalldruck sind, und zeigt über eine Frequenzkorrekturschaltung A-bewertete Schalldruckpegel an.
7. Übersicht Schallpegelmesser
7.1 Was ist ein Schallpegelmesser?
Schallpegelmesser sind Geräte zur Messung des A-bewerteten Schalldruckpegels ( L A ) und des Schalldruckpegels ( L p ) und werden nach dem Messgesetz als festgelegte Messgeräte bezeichnet. Spezifikationen und andere Details sind in IEC 61672-1 (entspricht „Präzisions-Schallpegelmesser“ im Messgesetz, JIS C 1509-1 Klasse 1) oder IEC 61672-1 (entspricht „Schallpegelmesser“ in der Messung) festgelegt Act, JIS C 1509-1 Class2) je nach Messgenauigkeit. Darüber hinaus gibt es integrierende Schallpegelmesser für integrierende Operationen wie z) und Schallbelastungspegel ( L AE ).
Hinweis:
IEC 61672-1 (JIS C 1509-1:2005) klassifiziert Schallpegelmesser je nach Leistung in Klasse 1 und Klasse 2. Klasse 1 und Klasse 2 entsprechen in etwa den Schallpegelmessern „Typ 1“ und „Typ 2“ in IEC 60651 (JIS C 1505 / JIS C 1502).
Methoden zur Messung und Bewertung verschiedener Arten von Lärm (Umwelt, Arbeitsumgebung, Fabrik/Verkehr, Shinkansen, Flugzeuge usw.) werden durch entsprechende Gesetze festgelegt. Lärmmessung ist ein wichtiger Bestandteil von Umweltbewertungen.

Abbildung 7.1: Größere Umweltmessgeräte, die als spezifizierte Messgeräte bezeichnet werden Vibrationspegelmesser
7.2 Unterschiede zwischen Schallpegelmessern (Klasse 2) und Präzisionsschallpegelmessern (Klasse 1)
Schallpegelmesser sind für die Messung von Umgebungsgeräuschen im Freien und an Orten wie Fabriken und Büros konzipiert. Sie sind preisgünstigere Modelle und können einfach vor Ort eingesetzt werden. Präzisions-Schallpegelmesser erfüllen alle Benutzeranforderungen für verschiedene Lärmstudien und die Bewertung von Maschinengeräuschen. Grundlegende Spezifikationen für beide Klassen basieren auf dem Measurement Act und JIS, die die folgenden Hauptunterschiede aufweisen.
IEC/ JIS
| Klasse 2 (Standard) | Klasse 1 (Präzision) | |
|---|---|---|
| Pegellinearitätsfehler (dB) (bei Eingangspegeländerung von 10 dB oder weniger) |
±0,8 (±0,5) | ±0,6 (±0,3) |
| Pegellinearitätsfehler (dB) (Andere als die oben genannten) |
±1,4 (±1,1) | ±1,1 (±0,8) |
| Frequenzbereich (Hz) | 20 bis 8 kHz | 16 bis 16 kHz |
Hinweis:
- Die Zahlen in Klammern berücksichtigen die erweiterte Messunsicherheit (entspricht dem maximal zulässigen Messfehler in IEC, JIS).
- Das Messgesetz legt die Differenz zwischen dem Mindestwert im Messbereich und dem Eigenrauschen wie folgt fest: Schallpegelmesser: +6 dB | Präzisions-Schallpegelmesser: +8 dB
7.3 Kalibrierung
Schallkalibratoren, die in IEC 60942 (JIS C 1515) spezifiziert sind, werden zum Kalibrieren von Schallpegelmessern einschließlich Mikrofonen verwendet.
Es gibt zwei Arten von Schallkalibratoren: den Kolbenphontyp, der den Referenzschalldruck unter Verwendung mechanischer Schwingungen mit festem Zyklus erzeugt; und der einfache Typ, der normale Konuslautsprecher. Ono Sokki bietet das Piston-Phone-Modell SC-3120 (IEC 60942:2003, JIS C 1515:2004 Klasse 1/C), das dynamische Lautsprechermodell SC-2500 (IEC 60942:2017, JIS C 1515:2004 Klasse 1) und das einfache Modell an Modell SC-2120A (IEC 60942:2003, JIS C 1515 Klasse 2). Der SC-3120 und SC-2500 erzeugen einen Schalldruck von 114 dB (250 Hz), während der SC-2120A 94 dB (1 kHz) erzeugt. Geben Sie vor Beginn der Messung den Referenzschalldruck des Schallkalibrators ein, stellen Sie die Frequenzbewertung entweder auf FLAT oder C ein und stellen Sie sicher, dass der Messwert mit dem Referenzschalldruck übereinstimmt. Verwenden Sie bei Bedarf den Einstellknopf, um Unstimmigkeiten zu beseitigen. Ein Unterschied von 2 dB oder mehr deutet auf einen Fehler hin;

Abbildung 7.2: Schaltkalibratoren
Die CAL-Taste eines Schallpegelmessers dient dazu, innerhalb des Schallpegelmessers stabile 1000-Hz-Kalibriersignale zu erzeugen, die 1/2 (= −6 dB) der vollen Skala (100 %) des Pegelbereichs entsprechen, um die Funktion zu überprüfen des Stromkreises. Diese Signale dienen zur einfachen Routinekontrolle und als Kalibriersignale für extern angeschlossene Geräte wie Pegelschreiber und FFT-Analysatoren.
Hinweis:
- IEC 61672-1:2002 (JIS C 1509-1:2005) erlaubt nur die akustische Justierung mit Schallkalibratoren, die IEC 60942:2003 (JIS C 1515:2004) als Mittel zur Kalibrierung und Inspektion (Justierung) für Schallpegelmesser verwenden . Die Kalibrierung mit internen elektrischen Signalen (1-kHz-Sinuswellen-CAL-Signale) ist daher nicht die Standardform der Kalibrierung.
- Da das Mikrofon einer hohen elektrostatischen Belastung ausgesetzt ist, kann Feuchtigkeit elektrostatische Funken verursachen, die ein Loch in der Membran verursachen können.
7.4 Messbereiche von Schallpegelmessern (Linearitätsbereiche)
Die Pegellinearitätsfehler von Schallpegelmessern nach IEC 61672-1:2002 (JIS C 1509-1:2005) bei A-bewerteten, C-bewerteten und Z-bewerteten Schalldruckpegeln sind angegeben (unter Berücksichtigung der erweiterten Messunsicherheit). ) wie folgt:
| Präzisions-Schallpegelmesser der Klasse 1 | ±1,1 dB |
| Standard-Schallpegelmesser der Klasse 2 | ±1,4dB |
Die zulässigen Abweichungen von Schwankungen von +/-10 dB bei gegebenen Signalpegeln in Pegelbereichen werden (unter Berücksichtigung der erweiterten Messunsicherheit) wie folgt angegeben:
| Präzisions-Schallpegelmesser der Klasse 1 | ±0,6dB |
| Standard-Schallpegelmesser der Klasse 2 | ±0,8dB |
Wenn ein Signal eingegeben wird, das dazu führt, dass der Linearitätsfehler den zulässigen Variationsbereich überschreitet, wird „Over“ (Pegel zu hoch) oder „Under“ (Pegel zu niedrig) als Warnung außerhalb des Messbereichs angezeigt. Der Messbereich (Linearitätsbereich) eines Schallpegelmessers ist definiert als ein Arbeitsbereich, in dem „Über“ oder „Unter“ ohne Frequenzbewertung, Bereich oder Frequenz angezeigt wird. In Prospekten wird normalerweise der Linearitätsbereich bei 1 kHz als Nennangabe angegeben, da der Messbereich je nach den oben genannten Bedingungen variieren kann. Betriebshandbücher enthalten normalerweise eine Tabelle mit nominalen Ober- („Über“) und Unter- („Unter“) Grenzwerten bei den folgenden Frequenzen mit jedem Gewichtungstyp.
| Präzisions-Schallpegelmesser der Klasse 1 | 31,5 Hz, 1 kHz, 4 kHz, 8 kHz, 12,5 kHz |
| Standard-Schallpegelmesser der Klasse 2 | 31,5Hz, 1kHz, 4kHz, 8kHz |
7.5 Windschutz
7.5.1 Warum ist ein Windschutz notwendig?
Ein Windschutz reduziert Windgeräusche um das Mikrofon herum. Am Mikrofon angebracht, reduziert ein idealer Windschutz Windgeräusche erheblich, ohne die akustischen Eigenschaften des Mikrofons stark zu beeinträchtigen. Windmikrofone werden im Allgemeinen in zwei Typen eingeteilt: der Allzwecktyp (normalerweise kugelförmig und aus Urethanschaum), der für Messungen einfach installiert und dann entfernt werden kann und der das Mikrofon vor Staub und anderen Fremdkörpern schützt und gleichzeitig äußere physikalische Einflüsse verringert Einschlag; und der Allwettertyp für erweiterte, kontinuierliche Messung von Flugzeug-, Fabrik- und anderen Arten von Geräuschen, der Windgeräusche erheblich reduziert und gleichzeitig widerstandsfähig gegen Regen, Schnee und andere Elemente ist. Für Lärmmessungen im Freien werden Windschutze empfohlen.
7.5.2 Leistung von Allzweck-Windschutzscheiben
In den meisten Fällen werden Allzweck-Windschutze an Handmikrofonen verwendet. Ein solcher Windschutz muss in der Lage sein, Windgeräusche auf ein bestimmtes Maß zu reduzieren, sich leicht am Mikrofon anbringen und wieder abnehmen lassen und im Design zum Mikrofon passen.
Die Windgeräuschreduzierungswirkung eines Windschutzes kann als Differenz zwischen dem Geräuschpegel ausgedrückt werden, der um das Mikrofon herum erzeugt wird, wenn es direkt vom Wind getroffen wird, und dem Geräuschpegel, der um das mit dem Windschutz bedeckte Mikrofon herum erzeugt wird. Der Effekt der Windgeräuschreduzierung hängt bekanntermaßen von der Größe der Windschutzscheibe ab.
Durch die Verdopplung des Durchmessers des Windschutzes ergibt sich eine Geräuschreduzierung von rund 6 dB. Die Schallpegelmesser von Ono Sokki werden mit einem der beiden Windschutztypen geliefert, je nachdem, welcher für das Messgerät besser geeignet ist. Die Serien LA-1410, LA-1440 und LA-4440 werden mit einem φ70 mm Windschutz geliefert. Die Serien LA-2111 und LA-5000 werden mit einem φ90 mm Windschutz geliefert. Abbildung 7-4 zeigt die Leistung dieser Bildschirme. Bei der Messung von Umgebungsgeräuschen im Freien (60 dB oder mehr) kann ein φ70-mm-Windschutz und ein φ90-mm-Windschutz bis zu einer Windgeschwindigkeit von etwa 3 m/s bzw. 5 m/s effektiv verwendet werden.

Abbildung 7.3: Windschutzleistung

Abbildung 7.4: Windschutz am Schallpegelmesser LA-1400
7.5.3 Allwetter-Windschutz
Allwetter-Windschutze werden für Außenmessungen bei Schnee, Regen oder anderen schlechten Wetterbedingungen empfohlen. Abbildung 7-6 zeigt ein Beispiel für den Allwetter-Windschutz (Option) von Ono Sokki, der mit einem Schallpegelmesser verbunden ist. Wie in der Abbildung gezeigt, wird auch ein Verlängerungskabel benötigt, um das Mikrofon mit dem Schallpegelmesser zu verbinden.

Abbildung 7.5: Allwetter-Windschutz am Schallpegelmesser
8. Struktur des Schallpegelmessers
8.1 Blockdiagramm
Abbildung 8.1 zeigt das Blockschaltbild für die elektrische Schaltung eines Schallpegelmessers. Die Positionen von AC out und DC out sind wichtig für das Verständnis und die optimale Nutzung eines Schallpegelmessers.

Abbildung 8.1: Blockschaltbild eines Schallpegelmessers
8.2 Mikrofon und Vorverstärker
High-End-Stereoanlagen geben den Originalklang von kleinen bis großen Lautstärken und von niedrigen bis zu hohen Frequenzen originalgetreu wieder. Eine naturgetreue Wiedergabe erfordert, dass der Originalton genau empfangen wird. Andernfalls ist der reproduzierte Ton nicht derselbe wie der Originalton. Die Aufgabe eines Mikrofons besteht darin, den Originalton genau zu empfangen und in elektrische Signale umzuwandeln. Diese Mikrosignale werden dann auf bestimmte Pegel verstärkt und die Impedanz wird von einem Vorverstärker richtig eingestellt. Schall ist definiert als Luftwellen mit abwechselnd hoher und niedriger Dichte. Als Sensoren zum Umwandeln von Eingangssignalen in elektrische Signale proportional zu den wechselnden Luftdichten (augenblicklicher Schalldruck) müssen das Mikrofon und der Vorverstärker eine hohe Empfindlichkeit und gute Frequenzeigenschaften aufweisen.

Abbildung 8.2: Aufbau eines Kondensatormikrofons
Mikrofone werden grob in drei Typen eingeteilt: Kondensatortyp, dynamischer Typ und Keramiktyp. Kondensatormikrofone werden für Schallpegelmesser verwendet, weil sie in akustisch vorteilhaften Formen mit kleinem Durchmesser hergestellt werden können, ein flaches Profil über einen weiten Frequenzbereich haben und stabiler als die anderen Mikrofontypen sind. Abbildung 8-2 zeigt zwei Typen von Kondensatormikrofonen, nämlich den Bias-Typ und den Back-Elektret-Typ. Ein Hauptunterschied zwischen den beiden Typen besteht darin, dass der Bias-Typ eine Gleichspannung an die Vibrationsmembran anlegt, während der Back-Elektret-Typ einen hinteren Pol verwendet, über dem ein dauerhaft elektrolysierter Polymerfilm angebracht ist, anstatt eine Spannung anzulegen. Im Allgemeinen ist der Bias-Typ empfindlicher als der Back-Elektret-Typ. Schließlich gilt für Mikrofone, die für Schallpegelmesser ausgelegt sind,
8.3 Frequenzbewertung Z- (oder FLAT-), A- und C- Bewertung
Für die Geräuschmessung ist die absolute Messung von Schalldruckpegeln über hörbare Frequenzbereiche hinweg unerlässlich. Allerdings variiert die menschliche Hörempfindlichkeit mit der Frequenz, und es ist nicht möglich, die Hörlautstärke einfach durch die Verwendung von quadratischen Mittelwert-Schalldruckwerten zu erklären. Die in 6-4 erläuterten Konturen gleicher Lautstärkepegel (ISO 226) zeigen Kurven gleicher Lautstärke (Schalldruckpegel) über verschiedene Frequenzen hinweg. Abbildung 8-3 zeigt Bewertungslinien, wobei die A-bewertete Linie einen niedrigen Schalldruckpegel und die C-bewertete Linie einen hohen Schalldruckpegel annähert. Früher wurden diese Leitungen zur Geräuschmessung mit entsprechender Lautstärke verwendet. Spätere Studien ergaben jedoch, dass diese Linien zwar die Lautstärke anzeigen, aber nicht geeignet sind, die Belästigung durch Geräusche darzustellen. und dass die A-bewertete Linie für hohe Schalldruckpegel verwendet werden kann. Heutige Schallpegelmesser sind nicht nur mit A- und C-Bewertung ausgestattet, sondern auch mit einer Z-Bewertung (oder FLAT-Bewertung), die ein flacheres Profil über die Frequenzen hinweg hat. Zur Geräuschpegelmessung wird immer eine A-Bewertungseinrichtung verwendet. Für schwankende Geräusche, die in einer Messung nicht genau gemessen werden können, ist der äquivalente kontinuierliche A-bewertete Schalldruckpegel (L Aeq ), basierend auf der durchschnittlichen Energie über viele Stunden, und Perzentil-Schalldruckpegel ( L X ), basierend auf der kumulativen Frequenzverteilung, werden verwendet. Mit einem flacheren Profil über die Frequenzen wird die C-Bewertung zur Aufzeichnung des Wechselstromausgangs von Schallpegelmessern und zur Messung von Impulsgeräuschen (mit einem breiteren Frequenzbereich) verwendet. Mit einem flachen Profil über einen breiteren Frequenzbereich als die C-Bewertung kann die Z-Bewertung (oder FLAT-Bewertung) als Allzweck-Akustiksensor verwendet werden, wobei die AC-Ausgangsfunktion und das Mikrofon und der Verstärker mit guten Frequenzeigenschaften genutzt werden.

Abbildung 8.3: Frequenzbewertung (A, C und Z)
Hinweis: Z-Gewichtung und FLAT-Gewichtung
Die bei früheren Schallpegelmessern angebotene "FLAT-Bewertung" bezog sich auf Frequenzcharakteristiken ohne Frequenzbewertung oder "FLAT"-Frequenzcharakteristiken. Jeder Hersteller hatte seinen eigenen Frequenzbereich und andere Spezifikationen für das Feature, mit dem Ergebnis, dass es praktisch keine Standards zur FLAT-Bewertung für Schallpegelmesser auf dem Markt gab. Andererseits legt IEC 61672-1:2002 (JIS C 1509-1:2005) neu die "Z-Bewertung" fest und fordert für diese Funktion eine Ebenheit zwischen 10 Hz und 20 kHz. Unter Berücksichtigung zulässiger Schwankungen und anderer Faktoren ist die FLAT-Gewichtung jedoch praktisch gleich der Z-Gewichtung, wie sie bisher als solche behandelt wurde.
8.4 Schnelle und langsame Zeitbewertung
Die Zeitgewichtung bezieht sich auf Spezifikationen der Anzeigebewegung (einschließlich digitaler Ablesung). Insbesondere entspricht es der Zeitkonstante für die Mittelwertbildung durch die in Abbildung 8-4 gezeigte quadratische Mittelwert-Erfassungsschaltung. Diese dynamische Eigenschaft (Zeitkonstante) ist in IEC 61672-1:2002 (JIS C 1509-1:2005) detailliert beschrieben. Es gibt die Zeitbewertung F (schnell: 125 ms) und die Zeitbewertung S (langsam: 1 s). Die Zeitbewertung F entspricht ungefähr dem Zeitverhalten der Ohren. Die Zeitbewertung S wird verwendet, um den durchschnittlichen Pegel des fluktuierenden Rauschens anzugeben. Die Zeitbewertung F wird normalerweise zum Messen von Rauschen verwendet. Da die Lautstärke von Impulsgeräuschen mit der Zeitbewertung F nicht genau gemessen werden kann, wird dafür die Zeitbewertung I (Impuls) (Anstieg: 35 ms, Abfall: 1,5 s) verwendet. In neueren Studien jedoch Es hat sich herausgestellt, dass die I-Zeitbewertung nicht so geeignet ist, um impulsiven Schall zu bewerten. Derzeit ist es in keiner der IEC (JIS) aufgeführt und ist nur in IEC 61672-1:2002 Anhang C (informativ) enthalten (JIS C 1509-1:2005, beigefügtes Dokument C). Stattdessen gibt es einen wachsenden Trend zur Verwendung des momentanen Spitzenschalldrucks als Parameter zur Bewertung von Impulsgeräuschen.

Abbildung 8.4: Zeitgewichtungs- und Effektivwert-Erkennungsschaltung
Abbildung 8-5 zeigt Pegelschwankungen, wenn 1-kHz-Ton-Burst-Signale (200-ms-Bursts in Intervallen von 3 s) in schnelle und langsame Zeitkonstanten eingegeben werden.

Abbildung 8.5: Einschwingverhalten der Zeitbewertung (Schnell und Langsam) (Logarithmische Skala auf der vertikalen Achse)
-
Zeitbewertung F (Schnell): Schnelle Werte entsprechen ungefähr dem Zeitverhalten der Ohren, und die Zeitkonstante für Anstieg/Abfall beträgt 125 ms.
-
Zeitgewichtung S (Slow): Slow-Eigenschaften werden verwendet, um den durchschnittlichen Pegel fluktuierender Geräusche anzuzeigen, und die Zeitkonstante für Anstieg/Abfall beträgt 1 s.
Die in Abbildung 8.4 gezeigte quadratische Mittelwerterkennung entspricht der Verarbeitung von Signalen mit quadriertem momentanem Schalldruck durch einen RC-Tiefpassfilter erster Ordnung, wie in Abbildung 8-6 gezeigt. Die Zeitkonstanten für die oben erläuterte Fast- und Slow-Zeitbewertung entsprechen der Zeitkonstante (τ = RC) des Tiefpassfilters. Abbildung 8-7 zeigt Antwortwellenformen von Anstieg und Abfall, wenn, wie in Abbildung 8-5, Tonburstsignale in diese Ersatzschaltung eingegeben werden. Wie in der Abbildung gezeigt, wo e i der quadratische Mittelwert einer stetigen Eingangssinuswelle ist, ist die Zeitkonstante τ wie folgt:
| Anstieg: Zeit, die etwa 63 % von e i entspricht |
| Abfall: Zeit, die etwa 37 % von e i entspricht |

Abbildung 8.6: Schaltung zur Erkennung des quadratischen Mittelwerts

Abbildung 8.7: Reaktionswellenformen, wenn Tonburstsignale in einen Tiefpassfilter erster Ordnung eingegeben werden (wobei e die Napier-Konstante ist (Basis des natürlichen Logarithmus), e = 2,71828 ...)
Abbildung 8.7 unterscheidet sich offensichtlich von Abbildung 8-5, in der die Y-Achse eine dB-Skala ist. Wenn Sie stattdessen eine lineare Skala verwenden, ist der Unterschied zwischen der Reaktionswellenform der schnellen Zeitbewertung und der langsamen Zeitbewertung jetzt viel klarer

Abbildung 8.8: Einschwingverhalten der Zeitbewertung (schnell und langsam) (mit linearer Skalierung auf der vertikalen Achse)
8.5 AC-Ausgang und DC-Ausgang
8.5.1 AC-Ausgang
AC out liefert elektrische Signale, die proportional zu der Schwankung des Luftdrucks (dh dem momentanen Schalldruck) sind, die von einem Mikrofon empfangen wird. Aufgrund der Beschaffenheit des Schalls liegen diese elektrischen Signale in Form von Wechselstrom vor, der seine Richtung in regelmäßigen Abständen ändert und die gleichen Eigenschaften wie 100 VAC (Wechselspannung, 50/60 Hz) für elektrische Haushaltsgeräte hat. Wie in Abbildung 8-1 gezeigt, werden Mikrofonsignale von der Frequenzkorrekturschaltung für die A-, C- und Z-Bewertung verarbeitet und von AC out gesendet. AC-Ausgangssignale werden hauptsächlich zur Frequenzanalyse von Schall mit Analysatoren (FFT-Analysatoren, Oktavanalysatoren usw.) oder zur Aufzeichnung von Geräuschpegeln mit Pegelschreibern verwendet. Es muss beachtet werden, dass AC-Ausgangssignale von der Frequenzgewichtung beeinflusst werden, obwohl sie nicht mit der Zeitgewichtung zusammenhängen.
Hinweis:
Einige Schallpegelmesser, wie z. B. die Serie LA-1400/4400 von Ono Sokki, verfügen über eine Funktion zur Bereitstellung von AC-Ausgangssignalen, die nicht frequenzbewertet (Z-Bewertung) sind, während sie frequenzbewertete Schalldruckpegel anzeigen.
8.5.2 DC-Ausgang
AC-Signale werden von der Schalldruckerkennungs-/Bewegungscharakteristikschaltung und der logarithmischen Berechnungsschaltung in DC-Spannungssignale in dB verarbeitet, die proportional zur dB-Anzeige auf dem Schallpegelmesser sind. In der Elektrizitätsterminologie sind DC-Signale das, was Sie erhalten, nachdem Sie quadratische Mittelwerte von AC-Signalen (momentaner Schalldruck) durch logarithmische Umwandlung in dB erhalten.

Abbildung 8.9: Amplitude und Effektivwert
Wie in Fig. 8-9 gezeigt, wird eine Wellenform (B) mit einer konstanten Höhe V 0 erhalten , indem eine Zeitwellenform (A) mit einer Amplitude von V A durch die Effektivwerterfassungs-/Bewegungskennlinienschaltung geschickt wird. V 0 ist der quadratische Mittelwert der Wellenform (A) und ist mit rms angehängt. Wenn (A) eine Sinuswelle ist, gilt die folgende Gleichung:
|
|
Indem der quadratische Mittelwert V 0 rms in (B) durch die logarithmische Berechnungsschaltung gegeben wird, werden DC-Ausgangsspannungssignale proportional zu 10 log 10 (V 0 rms) 2 erhalten. Wenn die Amplitude (V A ) der Wellenform (A) konstant ist, sind die DC-Ausgangssignale konstant. Wenn die Amplitude (V A ) der Wellenform (A) mit der Zeit schwankt, gilt dies auch für DC-Ausgangssignale (beeinflusst durch Zeitgewichtung).
Information:
Die AC- und DC-Ausgangsspannungen von Schallpegelmessern variieren von Modell zu Modell. Dies wird im Folgenden näher erläutert:
AC-Ausgang: 0,707 Veff/Vollausschlag
DC-Ausgang: 2,5 V/Vollausschlag, 0,5 V/10 dB
Wenn die oben genannten Nennwerte veröffentlicht werden, bedeutet dies:
-
"rms" bedeutet einen quadratischen Mittelwert.
-
"Skalenendwert" bedeutet den maximalen Wert eines Messbereichs. Bei einem Schallpegelmesser mit einem Messbereich von 30 bis 70 dB beträgt der Skalenendwert beispielsweise 70 dB.
-
„0,707 Vrms/Vollausschlag“ steht für das Verhältnis des AC-Ausgangs zum Messwert des Schallpegelmessers. Beispielsweise ist die Beziehung im Messbereich von 50 bis 90 dB wie folgt.
| Lektüre | AC aus |
|---|---|
| 90dB | 0,707 Vrms |
| 84dB | 0,707×10 (84-90)/20 = 0,354 Vrms |
| 58dB | 0,707×10 (58-90)/20 = 0,0178 Vrms |
Bei 0,707 Vrms beträgt die Amplitude ±1 V. Wenn die CAL-Taste am Schallpegelmesser gedrückt wird, werden Signale ausgegeben, die −6 dB/1 kHz Vollausschlag entsprechen. Da –6 dB (= 20 log 1/2) die Hälfte der vollen Skala sind, zeigt die Überwachung von CAL AC out Sinuswellen von ±0,5 V, 1 kHz.
-
"0,5 V/10 dB" steht für das Verhältnis von DC-Ausgang zum Schallpegelmesserwert. Beispielsweise ist die Beziehung im Messbereich von 30 bis 70 dB wie folgt.
| Lektüre | Gleichstrom aus |
|---|---|
| 70dB | 2,5 V |
| 64dB | 2,2 V |
| 60dB | 2,0 V |
| 30dB | 0,5 V |
Ein Messwert von 30 dB kommt mit 0,5 V (= 2,5 – 0,5 x (70 – 30)/10)
Schallpegelmesser mit einem großen Linearitätsbereich können eine negative Ausgangsspannung liefern, wenn der gemessene Schall extrem leise ist. Sowohl bei DC-Ausgang als auch bei AC-Ausgang sind Messwerte, die den Linearitätsbereich überschreiten, fehlerhaft und müssen als solche behandelt werden.
AC-Ausgangssignale sind Schwankungen des Schalldrucks und haben komplexe Wellenformen verschiedener Frequenzkomponenten. Rauschen kann wirksam gemildert werden, wenn seine Frequenzkomponenten geklärt werden. Aus diesem Grund werden AC-Ausgangssignale als Eingang in FFT-Analysatoren und Echtzeit-(Oktav-)Analysatoren verwendet.

Abbildung 8.10: AC-Out-Ausrüstung
FFT- und Echtzeit-(Oktav-)Analysatoren wandeln Signale in Schalldruckpegel um, analysieren sie für jede Frequenz und zeigen die Ergebnisse als Schalldruckpegel an.
AC-Ausgangssignale sind der momentane Schalldruck. Um AC-Ausgangssignale als Schalldruckpegel aufzuzeichnen, ist ein Pegelrekorder mit einer Effektivwert-Pegel-Umwandlungsschaltung erforderlich. Um Daten mit einem gewöhnlichen Stiftschreiber aufzuzeichnen, muss dieser an den DC-Ausgang angeschlossen werden. Bei FFT-Analysatoren entsprechen Zeitkonstanten zum Erhalten von quadratischen Mittelwerten ungefähr den FFT-Zeitfenstern und der Durchschnittszeit.
8.6 Anzeige
DC-Ausgangssignale werden auf dem Display als Schalldruckpegel basierend auf dem am Schallpegelmesser ausgewählten Messbereich angezeigt. Displays gibt es in analoger und digitaler Form: Analoge Displays verwenden eine Nadel, um Schalldruckpegel anzuzeigen, während digitale Displays numerische Zahlen oder eine Kombination aus numerischen Zahlen und Balkenanzeigen verwenden, um Schalldruckpegel anzuzeigen. Digitale Displays werden immer beliebter als analoge Displays. Abbildung 8-11 zeigt Beispiele digitaler Anzeigebildschirme auf den Schallpegelmessern von Ono Sokki.

Abbildung 8.11: Beispiele für die digitale Anzeige auf Schallpegelmessern von Ono Sokki
Abbildung 8-12 zeigt vereinfachte Diagramme, wie akustische Signale in digitale Formen umgewandelt werden. Digitale Zahlen geben Pegel pro Sekunde an. Balkenanzeigen zeigen analoge Pegel pro 100 ms.

Abbildung 8.12: Umwandlung akustischer Signale in digitale Formen
9. Ablesung des Schallpegelmessers
Schallpegelmesser messen Schall und zeigen ihn als Schalldruckpegel ( L p ) und A-bewerteten Schalldruckpegel ( L A ) an. Zusätzlich zu diesen Parametern berechnen und zeigen integrierende Schallpegelmesser den äquivalenten kontinuierlichen A-bewerteten Schalldruckpegel ( L Aeq ), den Schallexpositionspegel ( L AE ) und den prozentualen Schalldruckpegel ( L x ) an. Auf den folgenden Seiten wird beschrieben, wie jeder dieser Parameter bestimmt wird.
9.1 Schalldruckpegel ( L p )
Im akustischen Bereich ist der Schalldruckpegel ein physikalisches Maß für die Intensität (Schalldruck) von Schallwellen. Die Maßeinheit ist dB (dezi Bel).
Schall mit hohem Schalldruckpegel hat eine hohe Intensität; Schall mit niedrigem Schalldruckpegel hat eine geringe Intensität. Der Primärbereich des Schalldruckpegels beträgt 0 bis 130 dB. Es wird die Frequenzbewertung Z (FLAT) verwendet.
Der Schalldruckpegel ist wie folgt definiert.

Gleichung 9.1
Der Bezugsschalldruck p 0 ist der für den Menschen minimal hörbare Schalldruck, also 20 μPa = 2 × 10 -5 Pa. Der minimal hörbare Wert ist daher:

Gleichung 9.2
9.2 A-bewerteter Schalldruckpegel ( L A )
Dieser Parameter wird in Japan allgemein als "Rauschpegel" bezeichnet. Es ist der Schallpegel, ein physikalisches Schallmaß, kompensiert durch A-Bewertung. Als Maß für den Lärm wird der A-bewertete Schalldruckpegel, üblicherweise mit L A abgekürzt , verwendet, dessen Einheit dB (dezi Bel) ist. Das alte Messgesetz verwendete Phon als Maßeinheit; phon wurde später durch dB ersetzt, was im Schalldruckpegel gleich dB ist, um es an internationale Standards anzupassen. Als Referenzpegel gilt ein Schalldruckpegel von 40 dB bei 1 kHz. Die folgenden Kurven zeigen die Beziehung zwischen Schalldruckpegeln, die in Lautstärke und Frequenz als gleich empfunden werden. Diese Kurven werden Konturen mit gleichem Lautstärkepegel genannt. (Siehe Abschnitt 6.4, „Lautstärkepegel“.)

Abbildung 9.1: Frequenzbewertung und zulässige Bereiche
Hinweis: Schallpegel
IEC 61672 (JIS C1509 (Schallpegelmesser)) spezifiziert den frequenzbewerteten Schalldruckpegel als Schallpegel. Beispielsweise wird der A-bewertete Schalldruckpegel als A-bewerteter Schallpegel bezeichnet. Die Norm spezifiziert die folgenden drei Hauptschallpegelarten.
|
||
| 1 Zeitgewichteter Schallpegel | Schalldruckpegel, Geräuschpegel | |
| 2 Zeitlich gemittelter Schallpegel | Äquivalenter kontinuierlicher A-bewerteter Schalldruckpegel | |
| 3 Spitzenschallpegel | (Dies ist nicht der maximale Geräuschpegel.) |
Wie in Abbildung 8-1 (Blockschaltbild eines Schallpegelmessers) und Abbildung 8-12 (Umwandlung von akustischen Signalen in digitale Formen) gezeigt, ist der zeitgewichtete Schallpegel (1) der zeitgewichtete quadrierte momentane Schalldruckpegel. Gemäß IEC 61672 (JIS C1509) können der A-bewertete und der zeitbewertete Schallpegel mit der folgenden Gleichung ermittelt werden:

Gleichung 9.3

Gleichung 9.3 zeigt, wie der quadratische Mittelwert des frequenzbewerteten momentanen Schalldrucks berechnet wird, der dem A-bewerteten und zeitbewerteten Schallpegel oder dem konventionellen Geräuschpegel entspricht. Außerdem ist die Gleichung eine Funktion der Messzeit t, was anzeigt, dass der Schallpegel eine zeitabhängige Variable ist. Bei konstantem Rauschen bleibt der Schallpegel nahezu gleich. Bei zeitlich schwankendem Lärm ist der zeitlich gemittelte Schallpegel (2) zu ermitteln.
9.3 Äquivalenter kontinuierlicher A-bewerteter Schalldruckpegel ( L Aeq, T )
Dieser Parameter stellt schwankende Geräusche als durchschnittliche Energie dar und wird verwendet, um zu bewerten, wie lange Menschen welchen Geräuschpegeln ausgesetzt sind. Wie in Abbildung 9.2 gezeigt, zeigt der Parameter den durchschnittlichen Pegel der Gesamtenergie des Rauschens über einen bestimmten Zeitraum. Mit Fortschritten in der Lärmmesstechnik und internationalen Trends haben die überarbeiteten Umweltnormen für Lärm, die im April 1999 durchgesetzt wurden, einen äquivalenten kontinuierlichen A-bewerteten Schalldruckpegel ( L Aeq , T) als Parameter zur Bewertung von Umgebungslärm, und der Parameter ist seither ein wichtiger Indikator für Umgebungslärm. Der äquivalente kontinuierliche A-bewertete Schalldruckpegel stellt effektiv die physiologischen und psychologischen Reaktionen des Menschen auf fluktuierende Geräusche dar und stellt den physikalischen Pegel fluktuierender Geräusche als den Pegel konstanter Geräusche mit einer Energie gleich dem fluktuierenden Geräusch über die Messzeit T = t 2 − dar t 1.

Abbildung 9.2: Schwankendes Geräusch und äquivalenter kontinuierlicher A-bewerteter Schalldruckpegel
 Gleichung 9.4
Gleichung 9.4
Hinweis:
- Der äquivalente kontinuierliche A-bewertete Schalldruckpegel wird mit L Aeq, T abgekürzt .
- Der äquivalente kontinuierliche A-bewertete Schalldruckpegel entspricht dem A-bewerteten zeitlich gemittelten Schallpegel von IEC 61672-1:2002 (JIS C1509-1:2005).
9.4 Schallbelastungspegel ( L AE )
Dieser Parameter ist als Maß für ein einzelnes oder intermittierendes Geräusch von kurzer Dauer definiert. Wie in Abbildung 9-3 gezeigt, wird die Gesamtenergie eines einzelnen Tons in einen konstanten Ton umgewandelt, der eine Sekunde lang anhält und dessen Energie der Gesamtenergie des einzelnen Tons entspricht. Intermittierende Geräusche wie vorbeifahrende Züge und Pfähle, die gehämmert werden, werden für L AE gemessen , das dann in einen äquivalenten kontinuierlichen A-bewerteten Schalldruckpegel umgewandelt wird, der als Basisdaten für die Geräuschbewertung verwendet wird.

Abbildung 9.3: Schallbelastungspegel
Der Schallbelastungspegel ist wie folgt definiert.

Gleichung 9.5
Die Beziehung zwischen dem Schallexpositionspegel und dem äquivalenten A-bewerteten Dauerschalldruckpegel ist wie folgt.

Gleichung 9.6
Hinweis:
In IEC 61672-1:2002 (JIS C1509-1:2005) wird der Schallexpositionspegel als A-bewerteter Schallexpositionspegel bezeichnet und entspricht dem Energiepegel des zeitintegrierten Schalls.
9.5 Perzentil Schalldruckpegel ( L x )
Dieser Parameter wird seit vielen Jahren als Maß für schwankende Geräusche verwendet. Im Lärmschutzgesetz ist sie auch als Maß für Lärm aufgeführt. Der Parameter ist effektiv, um die Verteilung der Pegel von unregelmäßig und stark schwankendem Rauschen zu verdeutlichen. Unter Bezugnahme auf Abbildung 9-4, die schwankende Geräusche über einen Messzeitraum zeigt, gilt: Wenn die Gesamtzeit, in der das Geräusch einen bestimmten Pegel überschreitet, x % der Messzeit T = t 2 − t 1 beträgt, ist der Schallpegel gleich wird x % des Perzentil-Schalldruckpegels genannt und mit L x abgekürzt. Abbildung 9-5 zeigt die Beziehung zwischen dem prozentualen Schalldruckpegel (horizontale Achse) eines typischen schwankenden Geräuschs und dem Prozentsatz der Pegelüberschreitungszeit (vertikale Achse).
Hinweis:
In ISO 1996-1 (JIS Z 8731:1999) wird der Parameter mit LAN , T abgekürzt .

Abbildung 9.4: Schwankendes Geräusch und prozentualer Schalldruckpegel

Abbildung 9.5: Beziehung zwischen dem Perzentil-Schalldruckpegel und dem Prozentsatz der Pegelüberschreitungszeit
In der Praxis wird der prozentuale Schalldruckpegel erhalten, indem, wie in Abbildung 9-6 gezeigt, Proben des Geräuschpegels für jedes Zeitsegment Δt genommen und die Daten statistisch verarbeitet werden. In einer typischen Verarbeitung wird aus den Proben die Summenhäufigkeitsverteilung gewonnen und der Geräuschpegel mit einer prozentualen Häufung von (100 − x) % als x % des Perzentilschalldrucks bestimmt.
In Japan werden 50 % des Perzentil-Schalldruckpegels L 50 als mittlerer Schalldruckpegel, 5 % des Perzentil-Schalldruckpegels L 5 und 95 % des Perzentil-Schalldruckpegels L 95 als obere und untere Grenze der 90 % bezeichnet ( = 95 % – 5 %)-Bereich, und 10 % des Perzentil-Schalldruckpegels L 10 und 90 % des Perzentil-Schalldruckpegels L 90 werden als obere und untere Grenze des 80 %-Bereichs bezeichnet. Diese, zusammenfassend als die fünf Parameter bezeichnet, werden häufig zur Bewertung von fluktuierendem Rauschen verwendet. Bei der Messung des Perzentil-Schalldruckpegels werden normalerweise 50 Messungen durchgeführt, die jeweils fünf Sekunden dauern (Δt).

Abbildung 9.6: Schallpegelbeispiele und prozentualer Schalldruckpegel

Abbildung 9.7: Summenhäufigkeitsverteilung von Geräuschpegel und prozentualem Schalldruckpegel
9.6 Maximaler Schallpegel ( L max ) und minimaler Schallpegel ( L min )
Der maximale Schallpegel und der minimale Schallpegel über eine gegebene Messzeit werden als L max bzw. L min bezeichnet.

Abbildung 9.8: Schwankender Schallpegel und die maximalen und minimalen Werte
9.7 Maximalwert über N Sekunden (Tact max)
Augenblickswerte wie L p und L A zeigen Werte pro Sekunde aus den abgetasteten Daten, während Tactmax den Maximalwert aus den mit einer Sekunde abgetasteten Hochgeschwindigkeitsdaten anzeigt. In Japan werden Momentanwerte als Schallpegel verwendet, während in Europa normalerweise 1-Sekunden- oder 3-Sekunden-Tactmax verwendet wird.
Hinweis:
In der alten Norm IEC 60651 sind Momentanschalldruckpegel als maximaler Schalldruckpegel pro Sekunde (dh Tactmax 1 sec) definiert.

Abbildung 9.9: Gesampelter Schalldruckpegel und Tactmax (1 Sek.)
9.8 Spitzenschallpegel ( L - Spitze )
Ein Spitzenschallpegel ist der maximale absolute momentane Schalldruck (AC-Out-Wellenform) über einen Zeitraum, dargestellt auf einer logarithmischen Skala. Bei isolierten Burst-Signalen gibt es einen signifikanten Unterschied zwischen L Peak und dem maximalen Schallpegel ( L max ), wie in Abbildung 9-11 gezeigt. Bei stationären Sinuswellen zeigt L Peak die Amplitude der Sinuswellen (Spitzenwert) und L max den quadratischen Mittelwert, was eine Differenz von etwa 3 dB ergibt.

Gleichung 9.7
wobei f 0 der AC out -Wert ist, wenn der Referenzschalldruck ( Pa ) = 2 × 10 –5 und f A ( t ) max der Maximalwert der AC out (momentaner Schalldruck)-Wellenformen ist.

Abbildung 9.10: Änderung der Wellenform nach A-Bewertung von Eingangssignalen
f ( t ) : Eingangswellenform von isolierten Burst-Signalen
f A (t) : AC out-Wellenform von A-Bewertung gefiltert f ( t )

Abbildung 9.11: Unterschied zwischen den Spitzenwerten L max und L peak der Eingangssignale
L max : Maximalwert der DC -Ausgangswellenform
L peak : Maximaler (absoluter) logarithmischer Wert der f A (t) -Wellenform
Hinweis:
Maximaler Schallpegel und Spitzenschallpegel
Der maximale Schallpegel ( L max ) (siehe Abschnitt 9.6) wurde früher als Spitzenschallpegel bezeichnet. Heute sind sie voneinander verschiedene Parameter, wie unten zusammengefasst.
(2) Spitzenpegelwert ( L - Spitze )
- Das oben beschriebene Beispiel zeigt eine Änderung der Wellenform nach der A-Bewertung. Dies gilt auch für C- und andere Frequenzbewertungen.
- Es gab eine stärkere Nachfrage nach dem C-bewerteten Spitzenschallpegel L Cpeak zur Erfüllung der CE-Kennzeichnung.
- ISO 11200-Reihe (JIS Z8737-Reihe) „Lärm von Maschinen und Anlagen – Messung von Emissions-Schalldruckpegeln an einem Arbeitsplatz und an anderen festgelegten Positionen“ spezifiziert den Spitzen-Emissions-Schalldruckpegel L p , Spitze und als grundlegendes Maß C-bewerteter Spitzenschalldruckpegel L p Cpeak .
10. Verfahren zur Messung des äquivalenten kontinuierlichen A-bewerteten Schalldruckpegels (Übersicht über JIS Z8731:1999)
Grundlegende Messverfahren für Umgebungslärm sind in ISO 1996 (JIS Z 8731) festgelegt, die seit ihrer Einführung am 18. September 1957 in Japan weithin als Grundlage für die Messung und Bewertung von Lärm verwendet wird.
Mit dem wachsenden Bewusstsein für den Schutz der globalen Umwelt in den letzten Jahren gab es einen Trend zur weltweiten Vereinheitlichung von Bewertungsstandards. Als Teil davon wurden nationale Normen überarbeitet, um sie an ISO-Normen anzupassen, einschließlich der Überarbeitung des Messgesetzes von 1997, in der Phon durch dB ersetzt wurde, der Verabschiedung des Gesetzes über die Umweltverträglichkeitsprüfung von 1999 und der Überarbeitung von 1999 der Grundlegenden Umwelt Gesetz, in dem L 50 durch L Aeq ersetzt wurde .
JIS Z 8731 wurde ebenfalls überarbeitet, zuerst 1983 und basierend auf ISO 1996-1:1982 und ISO 1996-2:1983 erneut 1999. JIS Z 8731 wird auf den folgenden Seiten skizziert.
10.1 Äquivalenter kontinuierlicher A-bewerteter Schalldruckpegel
Umgebungslärm besteht aus mehreren Quellen, darunter Züge, Autos, Flugzeuge und Fabriken. Die Verteilung dieser Geräusche ändert sich sekündlich. ISO 1996 (JIS Z 8731) legt die Beschreibung und Messverfahren sowohl für einzelne Lärmquellen als auch für die gesamte Gruppe dieser Lärmquellen fest, die den Lärmzustand an einem bestimmten Ort bestimmen. ISO 1996 (JIS Z 8731) empfiehlt den äquivalenten kontinuierlichen A-bewerteten Schalldruckpegel als grundlegendes Bewertungsmaß zur Kontrolle von Umgebungsgeräuschen und zulässigen Geräuschgrenzwerten.
Durch die Annahme eines äquivalenten kontinuierlichen A-bewerteten Schalldruckpegels hat sich ISO 1996 (JIS Z 8731) dramatisch verändert. Zur Bestimmung des zulässigen Pegels einer bestehenden oder geplanten Lärmquelle sieht Anlage 1 für ein bestimmtes Gebiet die Erhebung von Schalldaten für eine zweckentsprechende Flächennutzung und die Beschreibung von Lärmpegeln aus Sicht des Umgebungslärms vor. Anhang 2 beschreibt, wie man den in der Vorrevision JIS Z 8731:1983 (Messmethoden und Beschreibung des A-bewerteten Schalldruckpegels) spezifizierten Perzentil-Schalldruckpegel für Referenzzwecke, die Beschreibung und Messung von bestimmten intermittierenden und impulsiven Geräuschen erhält, und das Verfahren der Hintergrundgeräuschkompensation für Dauergeräusche.
10.2 Begriffsdefinitionen
Im Folgenden finden Sie die Definitionen der Begriffe, die nicht in Kapitel 9 „Ablesung des Schallpegelmessers“ behandelt werden.
(1) Messzeitintervall
Eine Periode, während der das Rauschen als in einem stabilen Zustand betrachtet wird, wird als Beobachtungszeitintervall bezeichnet. Von einem Beobachtungszeitintervall wird eine Periode, während der das Rauschen tatsächlich gemessen wird, als Messzeitintervall bezeichnet.
(2) Bezugszeitintervall
Ein Intervall, für das ein äquivalenter kontinuierlicher A-bewerteter Schalldruckpegelwert als repräsentativer Wert verwendet werden kann, wird als Referenzzeitintervall bezeichnet, das unter Berücksichtigung der Lebensweise der Bewohner des Messbereichs und der Betriebszustände von Lärm festgelegt wird Quellen. Wenn beispielsweise ein Tag in Tag- und Nachtzeit unterteilt ist und die Tageszeit von 06:00 bis 22:00 Uhr läuft, sind die 16 Stunden zwischen diesen Zeiten das Referenz-Tageszeitintervall. Um einen äquivalenten kontinuierlichen A-bewerteten Schalldruckpegel für dieses Bezugstagesintervall zu erhalten, sollte der Schalldruckpegel idealerweise über die 16 Stunden hinweg gemessen werden. In der Praxis wird jedoch eine Anzahl von Intervallen innerhalb des Referenztagesintervalls zur Messung unter Verwendung von Stichprobentechniken ausgewählt. Zum Beispiel, Wenn ein Referenzzeitintervall in einstündige Segmente unterteilt wird, wird jede Stunde gemessen und als Beobachtungszeitintervall bezeichnet. Stichprobentechniken können auch auf Beobachtungszeitintervalle angewendet werden. Beispielsweise können Messungen während eines Teils eines Beobachtungszeitintervalls vorgenommen werden, beispielsweise zehn Minuten nach Beginn jeder Stunde. Ein Zeitraum, in dem der äquivalente kontinuierliche A-bewertete Schalldruckpegel kontinuierlich gemessen wird, wird als Messzeitintervall bezeichnet. Zur Berechnung eines äquivalenten kontinuierlichen A-bewerteten Schalldruckpegels eines Bezugszeitintervalls basierend auf so gemessenen Daten muss das Konzept der mittleren Energie verwendet werden. Eine erweiterte Version des täglichen Bezugszeitintervalls ist das langfristige Zeitintervall. Stichprobentechniken können auch auf Beobachtungszeitintervalle angewendet werden. Beispielsweise können Messungen während eines Teils eines Beobachtungszeitintervalls vorgenommen werden, beispielsweise zehn Minuten nach Beginn jeder Stunde. Ein Zeitraum, in dem der äquivalente kontinuierliche A-bewertete Schalldruckpegel kontinuierlich gemessen wird, wird als Messzeitintervall bezeichnet. Zur Berechnung eines äquivalenten kontinuierlichen A-bewerteten Schalldruckpegels eines Bezugszeitintervalls basierend auf so gemessenen Daten muss das Konzept der mittleren Energie verwendet werden. Eine erweiterte Version des täglichen Bezugszeitintervalls ist das langfristige Zeitintervall. Stichprobentechniken können auch auf Beobachtungszeitintervalle angewendet werden. Beispielsweise können Messungen während eines Teils eines Beobachtungszeitintervalls vorgenommen werden, beispielsweise zehn Minuten nach Beginn jeder Stunde. Ein Zeitraum, in dem der äquivalente kontinuierliche A-bewertete Schalldruckpegel kontinuierlich gemessen wird, wird als Messzeitintervall bezeichnet. Zur Berechnung eines äquivalenten kontinuierlichen A-bewerteten Schalldruckpegels eines Bezugszeitintervalls basierend auf so gemessenen Daten muss das Konzept der mittleren Energie verwendet werden. Eine erweiterte Version des täglichen Bezugszeitintervalls ist das langfristige Zeitintervall. Ein Zeitraum, in dem der äquivalente kontinuierliche A-bewertete Schalldruckpegel kontinuierlich gemessen wird, wird als Messzeitintervall bezeichnet. Zur Berechnung eines äquivalenten kontinuierlichen A-bewerteten Schalldruckpegels eines Bezugszeitintervalls basierend auf so gemessenen Daten muss das Konzept der mittleren Energie verwendet werden. Eine erweiterte Version des täglichen Bezugszeitintervalls ist das langfristige Zeitintervall. Ein Zeitraum, in dem der äquivalente kontinuierliche A-bewertete Schalldruckpegel kontinuierlich gemessen wird, wird als Messzeitintervall bezeichnet. Zur Berechnung eines äquivalenten kontinuierlichen A-bewerteten Schalldruckpegels eines Bezugszeitintervalls basierend auf so gemessenen Daten muss das Konzept der mittleren Energie verwendet werden. Eine erweiterte Version des täglichen Bezugszeitintervalls ist das langfristige Zeitintervall.
(3) Langfristiges Zeitintervall
Wenn ein gemessenes Referenzzeitintervallrauschen als wenig langzeitschwankend angesehen werden kann und die Messung als repräsentativer Wert verwendet werden soll, wird der betreffende Zeitraum als Langzeitzeitintervall bezeichnet.
(4) Langfristiger mittlerer Schallpegel ( L Aeq, LT )
Dies ist ein Wert, der die Reihe von Referenzzeitintervallen des äquivalenten Geräuschpegels im Langzeitzeitraum über den gesamten Langzeitzeitraum mittelt.
Der Durchschnittswert kann wie folgt berechnet werden.

Gleichung 10.1
(5) Bewertungsstufe ( L Ar, T )
Bei der Bewertung der menschlichen Reaktion auf Geräusche können anwendungsspezifisch korrigierte Messwerte als Ausgangsgröße herangezogen werden. Der Bewertungspegel ist ein äquivalenter kontinuierlicher A-bewerteter Schalldruckpegelwert, korrigiert um die Tonalität und Impulsivität des Objektlärms.

Gleichung 10.2
Die Tonalitätskorrektur K 1 i darf vorgenommen werden, wenn der gemessene äquivalente A-bewertete Dauerschalldruckpegel offensichtlich einen hörbar wahrgenommenen Reinton enthält, der durch eine 1/3-Oktavbandanalyse verifiziert wird und um 5 dB oder mehr größer ist als die angrenzenden Bänder. Eine Korrektur von 5 bis 6 dB ist möglich, wobei der Korrekturwert anzugeben ist. Wenn ein bestimmtes Geräusch in einem Zeitintervall als stark impulsiv angesehen wird, kann der in diesem Zeitintervall gemessene äquivalente kontinuierliche A-bewertete Schalldruckpegel korrigiert werden. Wenn das impulsive Geräusch nicht kontinuierlich, sondern isoliert ist, kann der äquivalente kontinuierliche A-bewertete Schalldruckpegel unter Ausschluss des isolierten Geräuschs bestimmt werden.
(6) Langfristiges durchschnittliches Ratingniveau ( L Ar, LT )
Dies ist die durchschnittliche Ratingstufe über ein langfristiges Zeitintervall der Ratingstufen, die über eine Reihe von Zeitintervallen berechnet wurden.

Gleichung 10.3
10.3 Arten von Geräuschen
Bei der Geräuschklassifizierung wurden wesentliche Änderungen vorgenommen. Während die bisherige Klassifikation allein auf der Schwankung des Lärmpegels über einen Zeitraum unabhängig von Lärmquellen beruhte, achtet die neueste Klassifikation genau auf die komplexe Zusammensetzung von Lärmquellen.
(1) Gesamtrauschen
An einem Ort gemessener Lärm besteht aus einer Reihe von Komponenten aus verschiedenen Quellen. Als solches ändert sich der Pegel des zusammengesetzten Rauschens auf komplexe Weise über einen Zeitraum. Ein solches zusammengesetztes Rauschen aus verschiedenen Quellen, das an einem Ort gemessen wird, wird als Gesamtrauschen bezeichnet, was früher als Umgebungsrauschen bezeichnet wurde.
(2) Spezifisches Rauschen
Während Gesamtrauschen aus Komponenten aus einer Reihe von Quellen besteht, besteht spezifisches Rauschen aus Komponenten, die aus diesen Quellen ausgewählt werden. Wenn wir uns beispielsweise unter verschiedenen städtischen Geräuschen wie denen von Verkehrssystemen und anderen täglichen Quellen auf Eisenbahnlärm konzentrieren, ist dieser Lärm in diesem Fall der spezifische Lärm.
(3) Hintergrundrauschen und Restrauschen
Wenn wir uns auf ein bestimmtes Geräusch oder bestimmte Geräusche unter dem Gesamtgeräusch konzentrieren, werden andere Geräusche als das/die bestimmte(n) Geräusch(e) des Gesamtgeräuschs kollektiv als Hintergrundgeräusch bezeichnet. Wenn wir uns beispielsweise an einer Messstelle auf den Eisenbahnlärm konzentrieren, gehört der Straßenlärm von nahe gelegenen Straßen zum Hintergrundgeräusch, auch wenn er lauter als der Eisenbahnlärm ist. Restgeräusch ist das, was vom Gesamtgeräusch übrig bleibt, nachdem alle spezifischen Geräusche, die stark zum Gesamtgeräusch beitragen, aus dem Gesamtgeräusch eliminiert wurden.
(4) Anfängliches Rauschen
Wenn sich die lokale Umgebung geändert hat, wie z. B. die Fertigstellung einer neuen Straße oder eines Hochhauses, wird der Gesamtlärm vor der Änderung als Anfangslärm bezeichnet.
(5) Klassifizierung von Geräuschen basierend auf Änderungen über einen bestimmten Zeitraum
Rauschen kann auf der Grundlage von Änderungen über einen bestimmten Zeitraum in beständiges Rauschen, fluktuierendes Rauschen, intermittierendes Rauschen und impulsives Rauschen (isolierter Ausbruch von Schallenergie und quasi-impulsives Rauschen) eingeteilt werden. Während die vorherige Version der Norm ein Messverfahren für jede Art von Lärm spezifizierte, besagt die neueste Norm, dass stationäre Geräusche und schwankende Geräusche durch gemessene äquivalente kontinuierliche A-bewertete Schalldruckpegel bestimmt werden müssen und dass intermittierende Geräusche und impulsive Geräusche bestimmt werden müssen durch den äquivalenten kontinuierlichen A-bewerteten Schalldruckpegel, der auf der Grundlage der Dauer und des Schallexpositionspegels des Lärms berechnet wird. (Siehe Kapitel 3.)
10.4 Schallpegelmesser und Kalibrierung
Schallpegelmesser müssen IEC 61672-1 (JIS C1509-1) für Präzisions-Schallpegelmesser der Klasse 1 oder mindestens IEC 61672-1 (JIS C1509-1) für Standard-Schallpegelmesser der Klasse 2 entsprechen. Praktisch sind Modelle, die in der Lage sind, den äquivalenten kontinuierlichen A-bewerteten Schalldruckpegel, den Schallexpositionspegel und den prozentualen Schalldruckpegel zu messen.
Schallpegelmesser müssen vor und nach einer Reihe von Messsitzungen vor Ort kalibriert werden, normalerweise unter Verwendung von Schallkalibratoren.
10.5 Messpunkt
Bei der Messung von Umgebungslärm müssen geeignete Messpunkte gemäß den gegebenenfalls geltenden Gesetzen ausgewählt werden. Während Messpunkte basierend auf Zweck, Inhalt, Ort und anderen Bedingungen der Messung ausgewählt oder bestimmt werden sollten, müssen im Allgemeinen die folgenden Regeln eingehalten werden.
(1) Im Freien
Bei der Messung von gewöhnlichem Umgebungslärm müssen Messpunkte mindestens 3,5 m entfernt von Gebäuden und anderen schallreflektierenden Objekten und 1,2 bis 1,5 m über dem Boden aufgestellt werden, um reflektierten Lärm zu eliminieren. Wenn es nicht möglich ist, Messpunkte in einem Abstand von 3,5 m oder mehr von Gebäuden usw. aufzustellen, ist es wünschenswert, Geräusche an Punkten zu messen, die möglichst weit von schallreflektierenden Gebäuden usw. entfernt sind Messung in der Nähe von Gebäuden etc. aufgestellt werden, ist dies anzugeben. Die bisherige Norm sah vor, dass bei der Messung von Fahrbahn- und anderen Straßengeräuschen Messpunkte am Ende des Gehsteigs neben der Fahrbahn oder, wenn kein Gehsteig vorhanden ist, am Ende der Fahrbahn und zusätzlich einzurichten sind 1,2 bis 1,5 m über dem Boden. Auf der anderen Seite. Dies gilt auch bei der Bewertung der Auswirkungen von bestimmten Geräuschen, etwa von Fabriken und Vergnügungsstätten in der Umgebung: Messpunkte müssen nach den örtlichen Gegebenheiten und gemäß den geltenden Gesetzen ausgewählt werden, vor allem aber an Stellen, an denen Lärm beanstandet wird.
(2) Lärmmessung rund um das Gebäude
Bei der Bewertung der Auswirkung von Außenlärm auf ein Gebäude müssen Messpunkte in einem Abstand von 1 bis 2 m von den Außenwänden des Gebäudes usw. sowie 1,2 bis 1,5 m über dem Bodenniveau des Stockwerks (der Stockwerke) eingerichtet werden Frage, um jeglichen Einfluss der Wände und anderer schallreflektierender Oberflächen zu eliminieren. JIS Z 8731:1983 legt fest, dass beim Messen von Geräuschpegeln vor einem Fenster ein Messpunkt 1 m vom Fenster entfernt auf der Mittellinie des Fensters aufgestellt werden muss.
(3) Lärmmessung innerhalb des Gebäudes
Bei der Messung von Schallpegeln innerhalb eines Gebäudes müssen Messpunkte mindestens 1 m von Wänden und anderen schallreflektierenden Flächen oder 1,5 m von Fenstern und anderen Öffnungen sowie 1,2 bis 1,5 m über dem Boden entfernt aufgestellt werden. Das Schallfeld in Innenräumen ist in den meisten Fällen äußerst komplex, was es wünschenswert macht, mehrere Messpunkte einzurichten und den Durchschnitt (arithmetischer Mittelwert oder Leistungsmittelwert) der Messungen zu bilden.
(4) Lärmmessung in der Arbeitsumgebung
Dieser Punkt wurde in JIS Z 8731:1999 gelöscht. JIS Z 8731:1983 und das Industrial Safety and Health Act legen fest, dass bei der Messung und Bewertung von Lärm in der Arbeitsumgebung in Fabriken, Büros und anderen Arbeitsplätzen Messpunkte an den Ohren des Bedieners eingerichtet werden müssen, sofern nicht anders angegeben, wenn der Bediener arbeitet meist am gleichen ort. Wenn sich der Bediener nicht am selben Ort aufhält, müssen Messpunkte an einigen der typischen Punkte auf dem Bewegungsweg des Bedieners sowie 1,2 bis 1,5 m über dem Boden eingerichtet werden. Messpunkte werden an Schnittpunkten eines 6 Meter mal 6 Meter großen Rasters aufgestellt.
(5) Einfluss meteorologischer Faktoren
Lärm kann durch Wetterbedingungen beeinflusst werden, insbesondere wenn er sich über eine längere Distanz ausbreitet. Wenn ein solcher Einfluss berücksichtigt werden muss, muss das Rauschen mit einer der folgenden Methoden gemessen werden.
(a) Mittelung der Ergebnisse von Messungen, die bei verschiedenen Wetterbedingungen durchgeführt wurden
Messzeitintervalle werden so eingestellt, dass ein langjähriger Mittelwert des Schallpegels bei verschiedenen Wetterbedingungen an Messpunkten ermittelt werden kann.
(b) Messungen bei bestimmten Wetterbedingungen
Die Messzeitintervalle werden so eingestellt, dass das gemessene Geräusch lauter ist, was normalerweise der Fall ist, wenn der Wind von der Geräuschquelle zum Messpunkt weht.
10.6 Methoden zur Lärmmessung
Mit dem Umweltgrundgesetz wurde das Bewertungskriterium vom mittleren Perzentil-Schalldruckpegel L 50 vollständig auf den äquivalenten A-bewerteten Dauerschalldruckpegel geändert. Mit dem Lärmschutzgesetz bleibt das Bewertungskriterium der Perzentil-Schalldruckpegel L 5 für bestimmte Anlagen, wurde aber im April 2000 auf den äquivalenten A-bewerteten Dauerschalldruckpegel für Autogeräusche geändert. Die folgende Tabelle zeigt Vergleiche zwischen dem äquivalenten A-bewerteten Dauerschalldruckpegel L Aeq und dem prozentualen Schalldruckpegel L 50 .
| Äquivalent kontinuierlich A-gewichtet ( L Aeq ) | Perzentiler Schalldruckpegel ( L 50 ) | |
| Grundlegende Eigenschaften | · Durchschnittliche Geräuschenergie | · Mittlerer Geräuschpegel |
| · Beeinflussbar durch impulsives und intermittierendes Rauschen (geringe zeitliche und räumliche Stabilität = hohe Empfindlichkeit) | · Schwer beeinflussbar durch impulsives und intermittierendes Rauschen (hohe zeitliche und räumliche Stabilität = geringe Empfindlichkeit) | |
| · Anpassungsfähig an schwankendes oder zusammengesetztes Rauschen | · Nicht anpassungsfähig an Rauschen mit unterschiedlichen Eigenschaften oder zusammengesetztes Rauschen | |
| · Nicht zum Vergleich zwischen Messungen verschiedener Geräusche geeignet | ||
| · Bei der Geräuschmessung mit gleichzeitiger Verwendung beider Parameter ergibt L Aeq normalerweise höhere Werte als L 50 , je nach Stärke der Geräuschschwankung unterschiedlich stark. | ||
| In Bezug auf die Reaktion der Anwohner | Spiegelt Expositionspegel von intermittierenden und anderen Geräuschen wider, was zu einer relativ hohen Korrelation mit der Reaktion der Bewohner führt | Weniger spiegelt zeitweilige Lärmexpositionspegel wider, was zu einer relativ geringeren Korrelation mit der Reaktion der Anwohner führt |
| Vorhersage | Bietet einen Zeitdurchschnitt der Rauschenergie, wodurch es erforderlich ist, nur die durchschnittliche Rauschenergie vorherzusagen, während die Notwendigkeit entfällt, die Rauschverteilung an den Vorhersagepunkten zu reproduzieren, wodurch die Vorhersageberechnung vereinfacht und klarer wird | Kann durch die Rauschverteilung beeinflusst werden, was es für eine genaue Messung erforderlich macht, die Rauschverteilung an den Vorhersagepunkten zu reproduzieren, wodurch die Vorhersageberechnung erschwert wird (obwohl einige Vorhersagen mit empirischen Formeln getroffen wurden) |
| Messung | Empfindlich gegenüber Schwankungen des Geräuschpegels; Wenn die Schwankung zu groß ist, muss die Messung über einen längeren Zeitraum durchgeführt werden, um stabile Daten zu erhalten (schwierig, sowohl Zuverlässigkeit als auch Praktikabilität zu erhalten). | Stabile Daten können durch Messungen kürzerer Dauer erhalten werden |
| Internationaler Trend | Von vielen Ländern und internationalen Gremien angenommen, erleichtert den weltweiten Vergleich von Daten | Extrem geringe weltweite Akzeptanz, was den globalen Vergleich von Daten erschwert |
Tabelle 10.1: Äquivalenter A-bewerteter Dauerschalldruckpegel L Aeq und prozentualer Schalldruckpegel L 50
Normalerweise erzeugt L Aeq je nach Stärke der Rauschschwankung in unterschiedlichem Maße höhere Werte als L 50 . Im Allgemeinen werden die folgenden Gleichungen verwendet, um den äquivalenten kontinuierlichen A-bewerteten Schalldruckpegel zu berechnen, sofern nicht anders angegeben.
Es ist möglich, den äquivalenten kontinuierlichen A-bewerteten Schalldruckpegel zu bestimmen, indem Daten in gleichen Intervallen auf dem Pegelschreiber notiert und Berechnungen unter Verwendung der Daten durchgeführt werden. Andererseits sind auf dem Markt digitale Schallpegelmesser erhältlich, die in der Lage sind, den äquivalenten kontinuierlichen A-bewerteten Schalldruckpegel und den prozentualen Schalldruckpegel gleichzeitig zu messen. Mit diesen Schallpegelmessern kann der äquivalente kontinuierliche A-bewertete Schalldruckpegel einfach berechnet werden.
(1) Schwankendes Rauschen
Bei der Messung von Lärm mit starken Schwankungen ist es wünschenswert, L Aeq mit integrierenden Schallpegelmessern zu messen. Denken Sie in diesem Fall daran, die tatsächliche Messzeit aufzuzeichnen. Andere praktische Verfahren umfassen Stichprobenverfahren und Verfahren, die eine statistische Verteilung von Geräuschpegeln verwenden.
(a) Stichprobenverfahren
Der äquivalente kontinuierliche A-bewertete Schalldruckpegel kann unter Verwendung der folgenden Gleichung basierend auf zwischen t 1 und t 2 in Δt-Intervallen abgetasteten Daten bestimmt werden.

Gleichung 10.4
Beachten Sie bei der Verwendung der Gleichung, dass die Genauigkeit beeinträchtigt werden kann, wenn das Abtastintervall (Δ t ) im Verhältnis zur Zeitkonstante für die Zeitgewichtung zu groß ist. Das Abtastintervall sollte 0,25 s oder weniger für die schnelle Zeitkonstante und 2 s oder weniger für die langsame Zeitkonstante betragen. Bei geringen Schwankungen und einem Messzeitintervall von mehreren Minuten oder mehr kann das Abtastintervall auf etwa 5 s erhöht werden.
(b) Verfahren unter Verwendung der statistischen Verteilung von Geräuschpegeln
Normalerweise kann der äquivalente kontinuierliche A-bewertete Schalldruckpegel unter Verwendung der folgenden Gleichung bestimmt werden, die auf der statistischen Verteilung von Geräuschpegelproben basiert, die in 5-dB-Segmente unterteilt sind.

Gleichung 10.5
(2) Konstantes Rauschen
Wenn der Messwert mit A-Bewertung und langsamer Zeitkonstante innerhalb von 5 dB liegt, kann das Rauschen als stetiges Rauschen behandelt werden. Der Messwert kann gemittelt und das Ergebnis verwendet werden, anstatt den äquivalenten kontinuierlichen A-bewerteten Schalldruckpegel mit integrierenden Schallpegelmessern zu bestimmen.
(3) Gleichmäßiges Rauschen mit stufenweiser Pegeländerung
Bei Dauergeräuschen, deren Pegel sich schrittweise ändert und die Stufen deutlich voneinander unterscheidbar sind, messen Sie es bei jedem Pegel als Dauergeräusch sowie die Dauer jedes Pegels. Dann kann unter Verwendung der Daten der äquivalente kontinuierliche A-bewertete Schalldruckpegel unter Verwendung der folgenden Gleichung berechnet werden:

Gleichung 10.6
(4) Isolierte Tonausbrüche
Bei im Umgebungslärm dominierenden Schallstößen kann anhand des Schallbelastungspegels der Stöße innerhalb der Zeit T der äquivalente A-bewertete Dauerschalldruckpegel nach folgender Gleichung ermittelt werden.

Gleichung 10.7
10.7 Informationen, die aufgezeichnet werden sollten
Zusätzlich zu den Ergebnissen der Schallmessung sollten auch die folgenden Informationen aufgezeichnet werden.
(1) Messmethoden
(a) Arten von Schallpegelmessern; Methoden zur Messung oder Berechnung
(b) Referenzzeitintervall, Messzeitintervall, Probenahmeintervalle, Zeiten usw. (falls Probenahme verwendet wird)
(2) Messbedingungen
(a) Atmosphärische Bedingungen: Windrichtung, Windgeschwindigkeit, Regen, Temperaturen am Boden und in anderen Höhen, atmosphärischer Druck, relative Luftfeuchtigkeit
(b) Arten und Bedingungen der Bodenoberfläche, Variabilität und andere Eigenschaften von Schallquellen, mit oder ohne spezifische Geräusche und, falls „mit“, deren Eigenschaften, Richtung usw.
(c) Messpunkte (Lage, Höhe)
10.8 Anhang 1 (Regeln): Erhebung akustischer Daten für eine angemessene Flächennutzung
Hinweis:
Anhang 1 (Regeln) von JIS Z 8731:1999 ist eine übersetzte Version von ISO 1996-2:1983
(1) Übersicht
Die Regeln legen Methoden zur Beschreibung des Umgebungslärms in bestimmten Gebieten sowie bestimmte Messverfahren zur Bewertung der Angemessenheit der Flächennutzung fest, die den gegenwärtig vorhandenen und den zukünftig zu erwartenden Lärm berücksichtigen. Die Regelungen werden voraussichtlich durch das Umweltverträglichkeitsprüfungsgesetz übernommen. Gebiete, in denen entweder der langjährige mittlere Schallpegel oder der langjährige mittlere Bewertungspegel zwischen einem bestimmten Bereich liegen, werden farblich gekennzeichnet und als 5-dB-Segment-Lärmpegelzonen in einem Höhenlinienformat auf der lokalen Karte angezeigt.
(2) Erhebung von Grunddaten
Folgende Grunddaten müssen erhoben werden.
(a) Lokale Topographie
(b) Statistische Jahresdaten zu Windrichtung, Windgeschwindigkeit, Niederschlag und Temperatur als Teil der Information über den Zustand der Anwohner und des Umlandes
(3) Akustische Daten
Repräsentative Werte für den Bewertungspegel, den Langzeitmittelwert des Schallpegels und den Langzeitmittelwert des Bewertungspegels für bestimmte Messpunkte sollten für jedes Zeitintervall ermittelt werden, wobei die Eigenschaften der Geräuschquellen und der Messpunkte zu berücksichtigen sind. Um die Schallpegelverteilung beurteilen zu können, sollte der prozentuale Schalldruckpegel ermittelt werden.
(3.1) Positionen und Anzahl von Messpunkten
Zur Beschreibung des jeweiligen Umgebungslärms geeignete Außenpunkte werden ausgewählt und unter Berücksichtigung der räumlichen Auflösung auf der Karte dargestellt. Zum Beispiel:
(a) Der gesamte zu messende Bereich wird in einem Raster angeordnet, wobei die Linien in gleichen Abständen und nahe genug beieinander liegen, um eine Differenz von 5 dB oder mehr an den Schnittpunkten und in der Nähe der Geräuschquelle zu vermeiden. Dann werden geeignete Messpunkte für die Messung ausgewählt.
(b) Es werden Messpunkte ausgewählt, die den Durchschnittspegel des spezifischen Bereichs darstellen.
(c) Es werden Messpunkte ausgewählt, die die Eigenschaften des von Quellen im Messbereich abgegebenen Lärms aufweisen.
(3.2) Positionen von Mikrofonen
Mikrofone müssen gemäß den in Abschnitt 10-5 beschriebenen Anforderungen für Messungen im Freien und in der Nähe von Bauwerken positioniert werden. In Gebieten, in denen voraussichtlich hohe Bauwerke gebaut werden, sollten bei Bedarf geeignetere Regeln festgelegt werden, z. B. die Positionierung von Mikrofonen in einer Höhe von 3 bis 11 m über dem Boden. Wenn Mikrofone nicht 3,5 m von Gebäuden entfernt positioniert werden können, können Messungen in 0,5 m Entfernung von offenen Fenstern durchgeführt werden. Wenn in 1 bis 2 m Entfernung von Außenwänden gemessen wird und die Messungen keinen dominanten Bandschall enthalten, können Werte, die 3 dB unter den Messungen liegen, als Schalldruckpegel für Fälle ohne Gebäude angesehen werden.
(3.3) Zeiteinstellung
(a) Referenzzeitintervall
Vorläufige Messungen sollten über lange Stunden durchgeführt werden, um das Referenzzeitintervall und das Messzeitintervall geeignet einzustellen. Das Referenzzeitintervall wird unter Berücksichtigung einer Reihe von Faktoren bestimmt, darunter typische Lebensweisen der Bewohner des Messgebiets und verschiedene Betriebsbedingungen von Lärmquellen.
(b) Langfristiges Zeitintervall
Das langfristige Zeitintervall wird so festgelegt, dass es langfristige Veränderungen des Lärmaufkommens unter Berücksichtigung des Zwecks des Lärmschutzes, der Eigenschaften des Messgebiets und der Lebensweise der Bewohner des Messgebiets widerspiegelt , Betriebsbedingungen von Geräuschquellen und Änderungen der Geräuschausbreitungsbedingungen.
(c) Messzeitintervall
Der äquivalente kontinuierliche A-bewertete Schalldruckpegel wird für die Geräuschart bestimmt, die in dem spezifischen Bezugszeitintervall gemessen wird. Vor diesem Hintergrund wird das Messzeitintervall basierend auf dem Auftreten von Geräuschen und Änderungen in der Ausbreitung und auf eine Weise festgelegt, die eine zuverlässige Auswahl des äquivalenten kontinuierlichen A-bewerteten Schalldruckpegels und eine genaue Schätzung des langfristigen durchschnittlichen Schallpegels und des langfristigen Durchschnitts gewährleistet Bewertungsstufe. Wenn der gemessene Lärm vorbeifliegende Flugzeuge, elektrische Züge und andere Transportmittel umfasst, wird das Messzeitintervall so festgelegt, dass der Schallexpositionspegel während der Durchfahrt dieser Transportmittel gemessen werden kann. Regen und starker Wind sind für die Geräuschmessung zu vermeiden. Für die Geräuschmessung müssen Wetterbedingungen gewählt werden, die zur Sicherstellung der Reproduzierbarkeit und stabilen Ausbreitung von Geräuschen beitragen. Wenn der zu messende Lärm dominante Schallquellen umfasst, werden die Messungen durchgeführt, wenn sich der Messpunkt windabwärts von der Lärmquelle befindet, die Windgeschwindigkeit 1 bis 5 m/s in 3 bis 11 m über dem Boden beträgt und keine nennenswerte Luft vorhanden ist Temperaturinversion in Bodennähe.
(3-4) Sammlung akustischer Daten
(a) Erfassung durch kontinuierliche Messung
Das Rauschen wird über das gesamte Bezugszeitintervall gemessen. Messungen dürfen nicht bei starkem Wind und/oder starkem Regen durchgeführt werden oder wenn Messungen stark durch Geräusche beeinflusst werden können, die für das Messgebiet nicht typisch sind, da diese Faktoren Messfehler erhöhen können.
(b) Erhebung durch Zeitstichprobe
Äquivalenter kontinuierlicher A-bewerteter Schalldruckpegel und Bewertungspegel werden basierend auf den Ergebnissen von Messungen bestimmt, die während diskreter Messzeitintervalle zwischen Referenzzeitintervallen durchgeführt wurden.
(4) Vorhersage des Geräuschpegels
Berechnungen oder maßstäbliche Modellversuche können verwendet werden, um die Lärmemission von Anlagen, die für den Bau geplant sind, wie Anlagen und von Straßenfahrzeugen, Flugzeugen, Eisenbahnen und anderen Transportmitteln, vorherzusagen.
(5) Beschreibungen der Lärmpegelzonen und -ergebnisse
Als Mittel zur Beschreibung der Ergebnisse aktueller Umgebungslärmmessungen und der Ergebnisse der Lärmvorhersage aus dem geplanten Betrieb wird eine Lärmpegelzone empfohlen. Diese Ergebnisse werden auf Karten von farbigen und schraffierten Zonen mit Konturen in 5-dB-Intervallen gezeigt. Jeder Messpunkt ist mit einem Kreis markiert, während jeder Vorhersagepunkt mit einem Kreuz markiert ist.
Farben und Schraffurmuster werden basierend auf den Werten von Geräuschpegelzonen bestimmt.
Zu den Elementen, die aufgezeichnet und gemeldet werden müssen, gehören Wetterbedingungen, Lärmquellen, Bodenoberflächenbedingungen, zu messende Flächen, Zwecke der Vorhersage und andere relevante Daten.
Hinweis:
Der Inhalt der Anlage 1 bezieht sich auf das später beschriebene Umweltverträglichkeitsprüfungsgesetz. Für verwandte Anwendungen bietet Ono Sokki die Umgebungslärmvorhersagesoftware SoundPLAN an (nur in Japan erhältlich).
10.9 Anhang 2 (Referenzen): Ergänzende Hinweise zur Beschreibung und Messverfahren für Umgebungslärm
Anhang 2 enthält eine Zusammenfassung der Methoden zur Bestimmung des Perzentil-Schalldruckpegels, der zur Beschreibung der zeitlichen Schwankungseigenschaften von Geräuschen, zur Beschreibung und Messung bestimmter intermittierender und impulsiver Geräusche und zur Korrektur des Einflusses von Hintergrundgeräuschen auf Dauergeräusche verwendet wird, die in JIS spezifiziert sind Z 8731:1983 (Meßverfahren und Beschreibung des A-bewerteten Schalldruckpegels).
Siehe Abschnitt 9.5 für Perzentil-Schalldruckpegel und Abschnitt 10.3 für Geräuscharten.
(1) Maßnahmen zur Beschreibung und Messung bestimmter intermittierender und impulsiver Geräusche
Spezifische intermittierende und impulsive Geräusche werden neben der im Hauptteil von JIS Z 8731 spezifizierten Messung des Schallbelastungspegels mit den folgenden Methoden beschrieben und gemessen. Der Einfluss von Hintergrundgeräuschen kann fast ignoriert werden, wenn eine Differenz von mehr als 10 dB vorhanden ist Ablesung des Schallpegelmessers zwischen intermittierendem oder impulsivem Lärm und wenn dies nicht der Fall ist. Wenn die Differenz weniger als 10 dB beträgt, kann das Dauerrauschen durch Hintergrundgeräusche beeinträchtigt werden, und daher muss eine Korrektur wie in (2) beschrieben vorgenommen werden. Es ist keine Korrektur erforderlich, wenn die Dauer des Hintergrundrauschens kurz ist.
(a) Spezifisches intermittierendes Rauschen

Abbildung 10.1: Ablesen des intermittierenden Geräuschpegels
Wie in Abbildung 10-1 gezeigt, wird jedes Mal, wenn Geräusche auftreten, der Höchstwert des Schallpegelmessers abgelesen. Die Bewegungseigenschaften des Schallpegelmessers sind auf Schnell eingestellt, sofern nicht anders angegeben. Wenn der Maximalwert nahezu konstant ist, wird der Mittelwert mehrerer Geräusche verwendet. Wenn sich der Maximalwert bei jedem auftretenden Geräusch stark ändert, wird ein repräsentativer Wert vieler Messungen wie die mittlere Energie und der Spitzenwert des 90 %-Bereichs der kumulativen Häufigkeitsverteilung ( L 5 ) bestimmt. Die verwendete Zeitgewichtung, die Häufigkeit des Auftretens von Geräuschen, die ungefähre Dauer jedes Geräuschs und andere relevante Daten werden aufgezeichnet.
(b) Spezifisches Impulsrauschen
-
Spezifischer isolierter Schallenergiestoß: Gemessen und beschrieben wie oben unter (a).
-
Spezifisches quasi-impulsives Geräusch: Der Höchstwert des schnellen zeitgewichteten Geräuschpegels wird auf dem Schallpegelmesser abgelesen.
(2) Korrektur des Hintergrundrauschens bei konstantem Rauschen
Bei der Messung des Pegels spezifischer Dauergeräusche kann das Hintergrundgeräusch nahezu vernachlässigt werden, wenn zwischen dem Auftreten des spezifischen Geräuschs und dem Nichtvorhandensein des Schallpegelmessers ein Unterschied von 10 dB oder mehr besteht. Das Hintergrundrauschen kann nicht ignoriert werden, wenn die Differenz weniger als 10 dB beträgt. In diesem Fall muss der Messwert gemäß der folgenden Tabelle korrigiert werden, um einen geschätzten Pegel des Dauerrauschens ohne Hintergrundrauschen zu erhalten.
| Unterschied beim Lesen zwischen Rauschen und keinem Rauschen | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|
| Korrekturwert | -2 | -1 | ||||
Tabelle 10.2: Differenz des Schallpegelmessers aufgrund des Einflusses von Hintergrundgeräuschen (Einheit: dB)
Hinweis:
Die Korrektur des durch das Hintergrundrauschen verursachten Messfehlers setzt voraus, dass sowohl das gemessene spezifische Rauschen als auch das Hintergrundrauschen stetiges Rauschen sind. Eine Korrektur ist oft bedeutungslos, wenn der Hintergrundgeräuschpegel in der Nähe des Pegels des gemessenen spezifischen Geräuschs schwankt.
[Ergänzung] Korrektur für Hintergrundgeräusche
ISO 1996-1 (JIS Z 8731: 1999 „Beschreibung und Messung von Umgebungslärm“) bezieht sich weitgehend auf Methoden zur Messung von Umgebungslärm im Allgemeinen und von Arbeitsumgebungslärm (zur Angleichung an ISO-Normen) und passt daher nicht in das Konzept „spezifisch“. Rauschen gegenüber anderem Rauschen (Hintergrundrauschen), mit dem Ergebnis, dass die Korrektur für Hintergrundgeräusche nicht in der Norm enthalten ist. Sein Anhang 2 enthält im Wesentlichen Zitate aus JIS Z 8731:1983 (Methods of Measurement and Description of A-weighted sound pressure level) und präsentiert sie als „Referenzmaterial“.
ISO 1996 (Reihe JIS Z 8737), die Verfahren zur Messung von Schalldruckpegeln abdeckt, die von Maschinen und Geräten ausgestrahlt werden, legt die Korrektur für Hintergrundgeräusche fest und definiert die Hintergrundgeräuschkorrektur K1 (positiver Wert) wie folgt.

Gleichung 10.8
wobei Δ L die Differenz zwischen dem gemessenen Schalldruckpegel der in Betrieb befindlichen Maschine und dem Hintergrundgeräuschpegel ist. Eine Korrektur ist möglich, wenn die Differenz einen bestimmten Pegel erreicht oder überschreitet (6 dB für technische Messungen und 3 dB für Vermessungsmessungen). Die Korrektur erfolgt durch Subtrahieren von K 1 von der Messung.
Gleichung 10.8 kann wie folgt erhalten werden.
Wenn L T der von der Maschine im Betrieb mit Hintergrundgeräuschen abgegebene Schalldruckpegel und L B der Hintergrundgeräuschpegel ist, beträgt der von der Maschine L S abgegebene Schalldruckpegel :

Gleichung 10.9

Gleichung 10.10
Daher ist die Hintergrundgeräuschkorrektur K 1 :

Gleichung 10.11
Abbildung 10.2 zeigt den Graphen, der Gleichung 10.8 darstellt.

Abbildung 10.2: Zusammenhang zwischen Δ L und Korrektur K 1
Tabelle 8.3: Vergleich zwischen alten und neuen JIS-Standards
| JIS (JIS Z 8731:1999) ISO1996-1:1982 -2:1983 | JIS (JIS Z 8731:1983) ISO1996-1:1982 * | |
| Geltungsbereich | · Zeigt Standardmethoden zur Beschreibung der Lautstärke von Umgebungslärm im Allgemeinen | · Zeigt Methoden zur Messung von Umgebungslärm im Allgemeinen und Arbeitsumgebungslärm |
| · Zeigt Standardmethoden für Umgebungslärm in Bezug auf Landnutzung | ||
| · Zeigt alte JIS-Beschreibungen für Konsistenz mit anderen Standards für Referenzzwecke | ||
| Parameter | A-bewerteter Schalldruckpegel: p A | A-bewerteter Schalldruck: p A |
| Schalldruckpegel: L p | A-bewerteter Schalldruckpegel: L A | |
| A-bewerteter Schalldruckpegel: L p A | Perzentilpegel: L x | |
| Perzentilpegel: L AN, T | Äquivalenter kontinuierlicher A-bewerteter Schalldruckpegel: L Aeq, T | |
| Schallbelastungspegel : L AE | Schallbelastungspegel : L AE | |
| Äquivalenter kontinuierlicher A-bewerteter Schalldruckpegel: L Aeq, T | ||
| Langfristiger mittlerer Schallpegel: L Aeq, LT | ||
| Bewertungspegel: L Ar, T | ||
| Langfristiger mittlerer Schallpegel: L Ar, LT | ||
| Terminologie | Messzeitintervall | Messzeitintervall |
| Referenzzeitintervall | Beobachtungszeitintervall | |
| Langfristiges Zeitintervall | ||
| Arten/Klassifizierungen von Geräuschen | · Typ | Umgebungsgeräusche, spezifische Geräusche, Hintergrundgeräusche |
| Gesamtrauschen, spezifisches Rauschen, Anfangsrauschen | ||
| · Einstufung nach zeitlicher Veränderung | Gleichmäßiges Rauschen, fluktuierendes Rauschen, intermittierendes Rauschen, impulsives Rauschen. | |
| Gleichmäßiges Geräusch, schwankendes Geräusch, intermittierendes Geräusch, impulsives Geräusch, isolierter Schallenergiestoß, quasi-impulsives Geräusch | Isolierter Ausbruch von Schallenergie, quasi-impulsives Rauschen | |
| Schallpegelmesser | Muss konform sein mit IEC 61672-1 (JIS C 1509-1 Klasse 1) (Präzisions-Schallpegelmesser), | JIS C 1505 (Präzisions-Schallpegelmesser) |
| IEC 61672-1 (JIS C 1509-1 Klasse 2) (Schallpegelmesser) | JIS C 1502 (Schallpegelmesser) | |
| JIS C 1512 (Pegelschreiber) | JIS C 1512 (Pegelschreiber) | |
| und in der Lage sein, den äquivalenten kontinuierlichen A-bewerteten Schalldruckpegel und Schallexpositionspegel zu messen. | oder andere Standards, die den oben genannten mindestens gleichwertig sind | |
| Mess-/Bewertungsmethoden | L Aeq, T wird basierend auf den folgenden Messungen bestimmt. | Konstantes Rauschen: Durchschnittlicher Messwert des Schallpegelmessers |
| · Schwankendes Rauschen: Integraler Mittelwert, Stichproben- oder statistisches Verteilungsverfahren | · Schwankungsrauschen: L Aeq, T oder L X | |
| · Stetiges Rauschen: Durchschnittlich langsames Lesen | · Spezifisches intermittierendes Rauschen: Peak Fast L A oder L AEeq, T basierend auf L AE berechnet | |
| · Rauschen mit stufenweiser Pegeländerung: Berechnet auf der Grundlage von konstantem Rauschen bei jedem Pegel und seiner Dauer | · Umgebungslärm einschließlich intermittierender Lärm: L Aeq, T | |
| · Einzelereignis-Schallbelastungspegel: Berechnet auf der Grundlage von L AE | · Spezifischer isolierter Schallenergiestoß: Peak Fast L A | |
| · Spezifisches quasi-impulsives Rauschen: Peak Fast L A | ||
| · Umgebungslärm einschließlich Impulslärm: L Aeq, T | ||
| Messpunkt | Im Freien: Ein Punkt, der mindestens 3,5 m von schallreflektierenden Objekten entfernt und, sofern nicht anders angegeben, 1,2 bis 1,5 m über dem Boden liegt | Im Freien: Ein Punkt 3,5 m oder mehr entfernt von schallreflektierenden Objekten und 1,2 bis 1,5 m über dem Boden. Auf der Straße, 1,2 bis 1,5 m über dem Boden, entweder am Ende des Bürgersteigs neben der Fahrbahn oder am Ende der Fahrbahn, wenn kein Bürgersteig vorhanden ist. |
| Um das Gebäude herum: Wenn nicht anders angegeben, 1 bis 2 m von der Außenwand des Gebäudes entfernt und 1,2 bis 1,5 m über dem Boden des Gebäudes | Um das Gebäude herum: 1 bis 2 m von der Gebäudeaußenwand entfernt und 1,2 bis 1,5 m über dem Gebäudeboden. Bei Messung vor einem Fenster, 1 m vom Fenster entfernt und auf dessen Mittellinie. | |
| Innerhalb eines Gebäudes: Sofern nicht anders angegeben, 1 m oder mehr entfernt von Wänden oder anderen schallreflektierenden Oberflächen, 1,5 m oder mehr entfernt von Fenstern oder anderen Öffnungen und 1,2 bis 1,5 m über dem Boden | Innerhalb eines Gebäudes: 1 m oder mehr entfernt von Wänden oder anderen schallreflektierenden Oberflächen und 1,2 bis 1,5 m über dem Boden. | |
| Arbeitsumgebung: Entweder an den Ohren des Bedieners oder 1,2 bis 1,5 m über dem Boden an typischen Stellen auf dem Bewegungsweg des Bedieners | ||
| Korrektur | Bewertungsstufe: Reintonkorrektur, Impulsrauschkorrektur | Korrektur von Hintergrundgeräuschen |
| Kalibrierung | Eine Kalibrierung mit einem Schallkalibrator ist erforderlich. |
*Die Philosophie von L Aeq in ISO 1996-1:1982 ist in JIS Z 8731:1983 enthalten.
10.10 Umgebungsbedingungen, die die Messung beeinflussen können
(1) Wetterbedingungen, Topographie und Oberflächengeometrie
Lärm, der sich im Freien ausbreitet, kann durch eine Reihe von Faktoren wie Topographie, Oberflächengeometrie und Wetterbedingungen wie Wind und Temperatur erheblich beeinflusst werden. Zum Beispiel wird Schall normalerweise in Bereichen vor dem Wind der Quelle lauter und in Bereichen vor dem Wind der Quelle weniger laut. Außerdem breitet sich Schall normalerweise weniger leicht aus, wenn die Temperatur in großen Höhen relativ niedriger ist als die Temperatur in niedrigen Höhen; und breitet sich leichter aus, wenn die Temperatur in großen Höhen relativ höher ist als die Temperatur in niedrigen Höhen. Schall, der sich über eine Bodenoberfläche mit größeren schallabsorbierenden Eigenschaften ausbreitet, wie etwa Reisfelder und Grasland, kann leichter gedämpft werden und sich daher weniger ausbreiten, als wenn er sich über schallreflektierende Oberflächen wie etwa Pflaster bewegt. Deshalb,
(2) Einfluss von Windgeräuschen
Windgeräusche entstehen, wenn starker Wind auf das Mikrofon eines Schallpegelmessers trifft. Wenn in diesem Fall der gemessene Schall kleiner als das Windgeräusch ist, ist das Signal-Rausch-Verhältnis nicht hoch genug, um eine Messung zu ermöglichen. Bei Lärmmessungen im Freien oder in der Nähe von Maschinen, die Wind erzeugen, muss ein Windschutz am Mikrofon angebracht werden. Die Messung sollte jedoch vermieden werden, wenn die Windgeschwindigkeit die Windgeräuschminderungskapazität des verwendeten Windschutzes übersteigt.
(3) Einfluss anderer Umweltbedingungen
Um elektrische Maschinen bilden sich häufig starke elektrische und magnetische Felder. Wenn Schallpegelmesser an solchen Orten aufgestellt werden, können die elektrischen Schaltkreise des Messgeräts und seines Mikrofons beeinträchtigt werden, wodurch die Messung möglicherweise ungenau wird. Wenn Mikrofonkabel mit Verlängerungskabeln verlängert werden, können diese Kabel leicht von diesen Feldern beeinflusst werden. Vibrationen, die von einer Reihe von Maschinen erzeugt werden, können auf den Schallpegelmesser übertragen werden und möglicherweise seine Leistung beeinflussen. Hohe Temperaturen und hohe Luftfeuchtigkeit können auch die Leistung von Schallpegelmessern und anderen Instrumenten beeinträchtigen.
Wie oben beschrieben, können Messungen durch eine Reihe von Faktoren beeinflusst werden, weshalb es unerlässlich ist, vor der Messung herauszufinden, ob es solche Faktoren gibt und wenn ja, welchen Einfluss sie auf die Messung haben können. Erwarteten Einflussfaktoren ist durch Abschirmungen, Schwingungsdämpfung und andere geeignete Maßnahmen entgegenzuwirken. Es ist auch wichtig, die Messpunkte sorgfältig auszuwählen.
10.11 Schallausbreitung und -dämpfung mit der Entfernung
Wie in Kapitel 1 beschrieben, breitet sich Schall (Schallwelle) mit etwa 340 m/s durch die Luft aus. Schall verliert seine Intensität (Schalldruckpegel), wenn er sich weiter ausbreitet, selbst wenn keine schallabschirmenden oder absorbierenden Materialien in der Nähe sind. Mit anderen Worten, Schall wird gedämpft, da er sich in alle Richtungen ausbreitet. Diese Schalleigenschaft wird Dämpfung mit der Entfernung genannt. Schall ist ein Wellenphänomen: Wenn er sich weiter von der Quelle entfernt, breitet sich der Schall über eine größere Fläche aus und daher wird die Intensität des Schalls (Schallenergie pro Flächeneinheit) schwächer. Bei Schall, der eine Punktquelle hat, breitet er sich kugelförmig im freien Raum aus. Es hat eine Fläche von 4πr 2(wobei r die Entfernung von der Schallquelle ist) und die Intensität des Schalls umgekehrt proportional zum Quadrat der Entfernung gedämpft wird. Dies wird als Abstandsquadratgesetz bezeichnet.
Wenn in Abbildung 10.3 die Schalldruckpegel im Abstand r 1 und im Abstand r 2 von der Punktschallquelle P gleich L 2 bzw. L 2 sind, gilt die folgende Gleichung.

Gleichung 10.11
Beispielsweise reduziert eine Verdoppelung des Abstands den Schalldruckpegel um 6 dB.

Abbildung 10.3: Schallausbreitung von einer Punktschallquelle und Dämpfung mit der Entfernung
11. Oktavbandanalyse (Frequenzanalyse)
Es gibt zwei Methoden zur Frequenzanalyse akustischer Schwingungen: Schmalbandanalyse (FFT-Analyse) und Oktavbandanalyse.
| Bandbreite der Analyse | Typische Anwendung | |
| FFT-Analyse | Konstante Bandbreite | Fehlerbehebung und Lösung von körperlichen Problemen |
| Oktavbandanalyse | Konstantes Bandverhältnis | Bewertung von Geräuschen und Vibrationen |
Tabelle 11.1: Frequenzanalysemethoden
Die Oktavbandanalyse wird auch als CPB-Analyse (Constant Percentage Bandwidth) bezeichnet. In den folgenden Abschnitten wird die Oktavbandanalyse erläutert.
11.1 Oktavbandanalyse
Um Lärmminderungsmaßnahmen zu erarbeiten, muss der Lärm analysiert werden (Frequenzanalyse). Eine der seit vielen Jahren eingesetzten Methoden zur Geräuschanalyse ist die Oktavbandanalyse. Eine Oktave ist eine Reihe von Noten, wobei die Note am oberen Ende der Reihe die doppelte Frequenz der Note am unteren Ende hat. (Siehe „Was ist eine Oktave?“ weiter unten.)
Die vom menschlichen Ohr wahrgenommene Frequenzcharakteristik ist eine geometrische, was die Oktavbandanalyse zu einem beliebten Analysemittel macht. Der Schalldruckpegel für jedes gemessene Geräuschband wird über den Audiofrequenzbereich hinweg unter Verwendung eines Bandpassfilters bestimmt, der 1/1-Oktav- oder 1/3-Oktav-Standards erfüllt. Für die Eigenschaften von Filtern und andere relevante Details siehe IEC 61260 (JIS C1514:2002).

Was ist eine Oktave?
Eine Oktave ist eine Reihe von Noten, wobei die Note, zB „do“, am oberen Ende der Reihe die doppelte Frequenz hat wie die Note, zB „do“, am unteren Ende der Reihe. Ein Oktavband ist ein Frequenzbereich von einer Oktave, der sich über eine Mittenfrequenz erstreckt, die als Mitten-Oktavbandfrequenz bezeichnet wird. Ein Drittel eines Oktavbandes wird als 1/3-Oktavband bezeichnet. Wie in der Abbildung rechts gezeigt, wird bei der gleichschwebenden 12-Ton-Stimmung eine Oktave in 12 Teile mit konstanten Verhältnissen zwischen den Frequenzen zweier benachbarter Töne unterteilt, wobei jeder Teil als 1/12-Oktavband bezeichnet wird.
11.2 JIS-Standards für Oktavfilter
Es gibt zwei JIS-Standards für Oktavfilter.
1. JIS C 1514:2002 (= IEC 61260:1995) Oktavband- und Teiloktavbandfilter
2. JIS C 1513:2002 Oktavband- und Terzband-Analysatoren für Schall und Schwingungen
JIS C1513:2002 legt notwendige und ausreichende Spezifikationen für Schall- und Vibrationsanalysatoren fest und verweist auf die JIS C1514:2002-Spezifikationen für die Eigenschaften von Oktav- und 1/3-Oktavfiltern. Sie legt nur Toleranzen der Klasse 1 und Klasse 2 fest, die steilere Eigenschaften aufweisen als die herkömmlichen Klassen Typ II und Typ III. Bei kleineren Zahlen gelten strengere Maßstäbe.| Mittenfrequenz (Hz) | 1/1 Oktave | 1/3 Oktave | Mittenfrequenz (Hz) | 1/1 Oktave | 1/3 Oktave | Mittenfrequenz (Hz) | 1/1 Oktave | 1/3 Oktave |
| 0,8 | ○ | 25 | ○ | 800 | ○ | |||
| 1 | ○ | ○ | 31. Mai | ○ | ○ | 1000 | ○ | ○ |
| 1.25 | ○ | 40 | ○ | 1250 | ○ | |||
| 1,6 | ○ | 50 | ○ | 1600 | ○ | |||
| 2 | ○ | ○ | 63 | ○ | ○ | 2000 | ○ | ○ |
| 2.5 | ○ | 80 | ○ | 2500 | ○ | |||
| 3.15 | ○ | 100 | ○ | 3150 | ○ | |||
| 4 | ○ | ○ | 125 | ○ | ○ | 4000 | ○ | ○ |
| 5 | ○ | 160 | ○ | 5000 | ○ | |||
| 6.3 | ○ | 200 | ○ | 6300 | ○ | |||
| 8 | ○ | ○ | 250 | ○ | ○ | 8000 | ○ | ○ |
| 10 | ○ | 315 | ○ | 10000 | ○ | |||
| 12.5 | ○ | 400 | ○ | 12500 | ○ | |||
| 16 | ○ | ○ | 500 | ○ | ○ | 16000 | ○ | ○ |
| 20 | ○ | 630 | ○ | 20000 | ○ |
Tabelle 11.2: Mittenfrequenzen von 1/1-Oktav- und 1/3-Oktav-Bandpassfiltern
11.3 Oktaven Filterbandbreite und Mittenfrequenz
1/1 und 1/3 Oktaven bestehen aus mehreren Frequenzbändern. Wenn:
f 1 die untere Grenzfrequenz ist,
f 2 die obere Grenzfrequenz ist und
f m die Mittenfrequenz ist,
dann gelten die folgenden Gleichungen für jedes Oktavband.
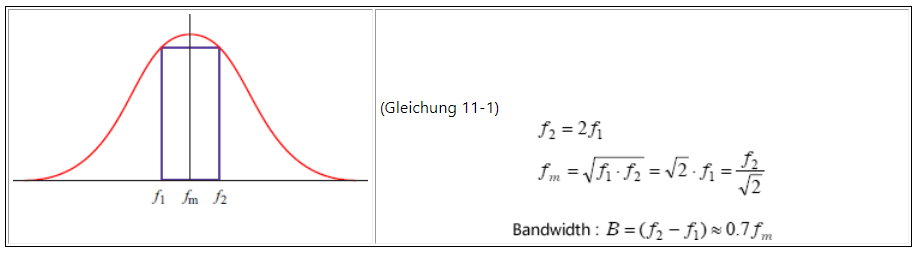
Abbildung 11.1: Mittenfrequenz, obere und untere Grenzfrequenz und Bandbreite des 1/1-Oktavbandes

Abbildung 11.2: Mittenfrequenz, obere und untere Grenzfrequenz und Bandbreite des 1/3-Oktavbandes
Ergänzung:
Mittenfrequenz
Im Folgenden wird kurz erläutert, wie die Mittenfrequenz f m bestimmt wird (Quelle: IEC 61260:1995 (JIS C1514)).
Gemäß IEC 61260 (JIS C1514) können genaue Mittenfrequenzen mit den folgenden Gleichungen bestimmt werden.
Wenn N eine ungerade Zahl ist (zB 1 oder 3)

....................
wo:
| fx _ | : Referenzfrequenz (1000 Hz) |
| x | : Ganzzahl (positiv, negativ oder 0) |
| N | : N von 1/N Oktavbandfilter zB 1 für 1/1 Oktave, 3 für 1/3 Oktave und 6 für 1/6 Oktave |
| G | Zahl, die das Oktavverhältnis darstellt (nominales Frequenzverhältnis von 2:1) |
Zur Bestimmung von G werden die beiden folgenden Methoden angegeben.
Gleichung 11.5: Zehnerpotenzen bilden

Gleichung 11.6: Zweierpotenzen bilden

Per Definition sollte die Nutzung der Befugnisse der 2. Form keine Einwände erheben. Die Potenzen der 10er-Form wurden aufgrund der Tatsache verwendet, dass 10 Oktaven fast gleich drei Dekaden sind (2 10 ≒ 10 3 ), was G 10 in Gleichung 11-5 zu etwa 2 (1,9953) macht. Die Potenz von 10 besteht aus Vielfachen von 10 und funktioniert auch gut mit Dezimalzahlen, was sich selbst zu einem empfohlenen System in Standards macht.
Hinweis:
Um genau zu sein, die "2" in Gleichung 11-1 und Gleichung 11-2 ist tatsächlich das oben dargestellte G, wird aber in diesen Gleichungen der Einfachheit halber und zum leichteren Verständnis verwendet.Wenn das N eines 1/N-Oktavfilters eine gerade Zahl ist, ist die Referenzfrequenz 1 kHz nicht in der Liste der Mittenfrequenzen enthalten, wie aus Gleichung 11-4 ersichtlich ist.
Die folgenden Abbildungen zeigen Eigenschaften von 1/1- und 1/3-Oktavbandfiltern (Quelle: JIS C1513)
Abbildung 11.3: Relative Dämpfungsgrenzen eines Oktavbandfilters der Klasse 1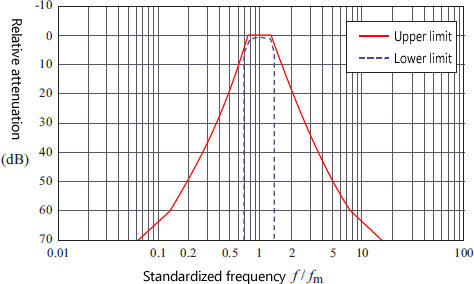
Abbildung 11.4: Relative Dämpfungsgrenzen des Oktavbandfilters der Klasse 2
Abbildung 11.5: Relative Dämpfungsgrenzen eines 1/3-Oktavbandfilters der Klasse 1
Abbildung 11.6: Relative Dämpfungsgrenzen eines 1/3-Oktavbandfilters der Klasse 2
Referenz:
Umwandlung von 1/3-Oktavdaten in 1/1- Oktavdaten
Wenn Sie bekannte 1/3-Oktavdaten in dB in entsprechende 1/1-Oktavdaten in dB umwandeln, addieren Sie die 1/3-Oktavdaten in dB, die den Ziel-1/1-Oktavdaten entsprechen. Wenn Sie beispielsweise die 1/1-Oktavbanddaten um die Mittenfrequenz von 1000 Hz herum bestimmen und das entsprechende 1/3-Oktavband die folgenden Daten in dB hat,
| 800 Hertz | 73dB |
| 1000 Hertz | 77dB |
| 1250 Hertz | 75dB |
die 1/1-Oktavbanddaten um die Mittenfrequenz von 1000 Hz herum können unter Verwendung der folgenden Gleichung bestimmt werden.

Gleichung 11.7
11.4 Berechnung des Gesamtpegels (Gesamtbandpegel)
Frequenzanalysatoren zeigen nicht nur den Geräuschpegel (Schalldruckpegel) für jedes Frequenzband, sondern auch die aggregierten Bandpegel oder den Gesamtpegel. Bei der Häufigkeitsanalyse wird je nach Zweck der Analyse eine Häufigkeitsgewichtung wie die A-Gewichtung angewendet oder nicht angewendet (FLAT-Gewichtung). Bei Verwendung von FLAT-bewerteten Daten zur Berechnung eines A-bewerteten Gesamtpegels kann eine Kombination aus Messungen für die einzelnen Bänder und den Korrekturwerten in Tabelle 11-3 (z. B. 55,2 dB bei 200 Hz korrigiert auf 44,3 (55,2 – 10,9) dB) verwendet werden verwendet werden, um den Zweck zu erfüllen. Wenn die Rauschpegel für einzelne Frequenzbänder L 1 , L 2 , ....... , L n (dB) sind, kann der Gesamtpegel L (dB) unter Verwendung der folgenden Gleichung bestimmt werden. (Diese Berechnung entspricht der Summe der dB-Werte in Abschnitt 12.1.)

Gleichung 11.8
Diese Methode wird häufig im Rahmen von Lärmminderungsmaßnahmen verwendet, um reduzierte Lärmpegel anhand einer Tabelle ähnlich Tabelle 11-3 vorherzusagen.
|
Mittenfrequenz | Korrekturwert (dB) |
Mittenfrequenz | Korrekturwert (dB) |
Mittenfrequenz | Korrekturwert (dB) |
|---|---|---|---|---|---|
|
12.5 |
-63,4 |
160 |
-13.4 |
2000 |
+1.2 |
|
16 |
-56,7 |
200 |
-10.9 |
2500 |
+1.3 |
|
20 |
-50,5 |
250 |
-8.6 |
3150 |
+1.2 |
|
25 |
-44,7 |
315 |
-6.6 |
4000 |
+1.0 |
|
31.5 |
-39.4 |
400 |
-4.8 |
5000 |
+0,5 |
|
40 |
-34.6 |
500 |
-3.2 |
6300 |
-0,1 |
|
50 |
-30.2 |
630 |
-1.9 |
8000 |
-1.1 |
|
63 |
-26.2 |
800 |
-0,8 |
10000 |
-2,5 |
|
80 |
-22.5 |
1000 |
0 |
12500 |
-4.3 |
|
100 |
-19.1 |
1250 |
+0,6 |
16000 |
-6.6 |
|
125 |
-16.1 |
1600 |
+1.0 |
20000 |
-9.3 |
Tabelle 11.3: A-Gewichtungstabelle
11.5 ALLPASS und GESAMT
Einige Oktavanalysatoren haben die Möglichkeit, ALL PASS- und OVERALL-Messwerte anzuzeigen. Sie haben die folgenden Bedeutungen.
Hinweis:
In vielen Fällen werden ALLPASS und OVERALL gleichbedeutend verwendet. Auf den Frequenzanalysatoren von Ono Sokki hingegen unterscheiden sich diese Begriffe deutlich, wie unten beschrieben.
(1) ALLPASS
Das Ablesen eines Werts, der durch Ausgabe von AC-Ausgangssignalen (momentaner Schalldruck) erhalten wird, nicht durch Frequenzanalyse, sondern durch Umwandlung in einen quadratischen Mittelwert, der dann durch logarithmische Umwandlung in einen dB-Pegel umgewandelt wird.
(2) GESAMT
Das Ablesen eines Werts, der durch Ausgeben von AC-Ausgangssignalen (momentaner Schalldruck) durch 1/1- und 1/3-Oktavanalysen und unter Verwendung der 1/1- und 1/3-Oktavbanddaten, Tabelle 11-3 und Gleichung 11-8, erhalten wird , Bestimmung des dB-Pegels.
Das obere Diagramm in Abbildung 11-7 zeigt die Ergebnisse der Z (FLAT)-gewichteten 1/3-Oktav-Analyse von gewöhnlichem Rauschen, bei der ALLPASS- und OVERALL-Werte nahezu gleich sind. Das untere Diagramm in Abbildung 11-7 zeigt einen A-gewichteten GESAMT-Wert der Daten im oberen Diagramm, der anhand von Tabelle 11-3 und Gleichung 11-8 berechnet wurde.

Abbildung 11.7: Vergleich der ALLPASS- und OVERALL-Werte in der 1/3-Oktavbandanalyse
Hinweis:
Obwohl die Werte ALLPASS und OVERALL voneinander abweichen können, sind sie dennoch effektive Werte. Seien Sie vorsichtig mit dieser Angelegenheit. Sie sind nahezu gleich (oder unterscheiden sich voneinander nur um 0,1 bis 0,2 dB), wenn gewöhnliches stationäres Rauschen analysiert wird, das transientes Rauschen nicht einschließt. Das Frequenzband von ALLPASS-Signalen deckt den gesamten Bereich der Eingangssignale ab (z. B. 20 Hz bis 20 kHz für Mikrofone), während das von OVERALL-Signalen das Zielfrequenzband abdeckt. In einem einzigartigen Fall, in dem der Rauschpegel bei etwa oder über 20 kHz deutlich höher ist, können die ALLPASS-Werte höher als normal sein. Bei den neuesten Schallpegelmessern erfolgt der gesamte Prozess innerhalb und nach der RMS-Schaltung (Effektivwert) (innerhalb der gepunkteten Linie im Blockdiagramm von Abbildung 8-1) durch digitale Berechnung. Dies ist im Blockschaltbild zwar nicht dargestellt,S (z. B. 64 kHz oder 48 kHz) je nach Typ des Schallpegelmessers ist das maximale Frequenzband (innerhalb 1/2 der Abtastfrequenz) der Eingangssignale begrenzt. ALLPASS-Werte beinhalten den Leistungswert des maximalen Frequenzbands. In einem besonderen Fall können ALLPASS-Werte von über 20 kHz Geräuschdaten von einem Schallpegelmessermodell zum anderen variieren.
Die zur Oktavanalyse fähigen Schallpegelmesser (LA-3570/3560/3260) von Ono Sokki haben nicht die Funktion, GESAMT-Werte zu berechnen, sondern die Funktion, zwei ALLPASS-Werte gleichzeitig mit unterschiedlicher Frequenz- und Zeitbewertung zu berechnen. Abbildung 11-8 zeigt ein Beispiel für zwei zusammen berechnete ALLPASS-Werte (Ap1 und Ap2).
Abbildung 11.8: Zwei ALLPASS (AP)-Werte zusammen angezeigt
Referenz
Frequenzanalyse niedriger Geräuschpegel
Bei der Frequenzanalyse der Geräuschpegel von geräuscharmen Maschinen oder Hintergrundgeräuschpegeln kann es vorkommen, dass ALLPASS- (oder GESAMT-) Werte in positiven dB angegeben werden, während Bandpegel in negativen dB angegeben werden. Negative Werte bedeuten, dass die Leistung kleiner als der Referenzwert (20 μPa) ist, die Rauschleistung aber nicht negativ ist. Beispielsweise ergibt das Addieren der Leistung der Bänder unter Verwendung von Gleichung 11-8 einen Wert gleich dem ALLPASS- (oder GESAMT-) Wert. Abbildung 11-9 zeigt die Rauscheigenschaften der Mikrofone von Ono Sokki. Während der OA-Wert bei etwa 11 dB liegt, liegen die Werte für die einzelnen Bänder bei etwa oder unter 0 dB.

Abbildung 11.9: Rauschverhalten von Mikrofonen (A-bewertet)
11.6 NC (Lärmkriterien)
NC wurde 1957 von LL Beranek, USA, als Bewertungsparameter vorgeschlagen, basierend auf den Ergebnissen einer großangelegten Felduntersuchung zum Bürolärm und einer Befragung von dort Beschäftigten im Rahmen einer Studie über Dauerlärm mit breitbandigem Spektrum wie Klimaanlagengeräusche. Der Schalldruckpegel des gemessenen Geräusches wird für jedes Oktavband aufgetragen, um eine NC-Kurve zum Vergleich mit einer Reihe von Referenzkurven in Abbildung 11-10 zu erstellen. Wenn die erstellte NC-Kurve für jedes Oktavband unterhalb einer Referenzkurve liegt, ist die Nummer dieser Referenzkurve die NC-Nummer für das Rauschen.

Abbildung 11.10: NC-Kurven
Abbildung 11.11 zeigt ein Beispiel für 1/1-Oktav-Analysewerte und NC-Messungen, die auf einem Schallpegelmesser von Ono Sokki angezeigt werden. Als Frequenzbewertung für solche Messungen wird die Z (FLAT)-Bewertung verwendet.

Abbildung 11.11: Beispiel einer NC-Nummernanzeige
11.7 Lautheitsanalyse (Loudness, Sharpness)
Der Lautstärkepegel ist ein Geräuschbewertungsparameter, der den akustischen Maskierungseffekt berücksichtigt, der beim A-bewerteten Schalldruckpegel (L A ) nicht berücksichtigt wurde und als solcher die vom Menschen wahrgenommene Lautstärke besser darstellt.
Heutzutage werden manche Haushaltsgeräte in Prospekten und verwandten Medien als „halb so laut wie herkömmliche Produkte“ angepriesen. Das Kriterium, das bei solchen Vergleichen verwendet wird, ist die Lautstärke.
Die Schallpegelmesser der LA-3000-Serie von Ono Sokki bieten eine Lautheitsanalyse basierend auf 1/3-Oktav-Analysedaten in Echtzeit. Ono Sokki bietet auch die Sound Quality Evaluation-Software an, die den Klang anhand von sechs psychoakustischen Parametern wie Schärfe, Rauheit, Schwankungsstärke, KI, Tonalität und Lautstärke quantifiziert.
(1) Was ist Lautstärke?

Abbildung 11.12: Konzepte der psychoakustischen Bewertung
Wenn wir Geräusche hören, spielen eine Reihe von Faktoren eine Rolle, wie in Abbildung 11.12 dargestellt. Wie wir über das Geräusch, das wir hören, denken, hängt von unseren psychischen Bedingungen ab und ist von Person zu Person unterschiedlich: Manche Menschen haben nichts gegen ihnen vertraute Geräusche. Es wurden viele Versuche unternommen, den Klang unter Berücksichtigung psychologischer Faktoren zu bewerten. Ono Sokki hat zu diesem Zweck die Soundqualitäts-Bewertungssoftware OS-2000 verwendet.
Aus Sicht des Hörsinns ist die Lautstärke, die einer der Bewertungsparameter für die Klangqualität ist, stark vom Schalldruckpegel abhängig. Der A-bewertete Schalldruckpegel, der üblicherweise zur Bewertung von Geräuschen verwendet wird, wurde als Schalldruckpegel mit einer Frequenzbewertung entwickelt, die an 40-Phon-Reintonlautstärken angenähert ist (Konturen mit gleicher Lautstärke (ISO R 226)), um das Hören zu simulieren Sinn. Wenn jedoch zwei verschiedene reine Töne mit der gleichen Lautstärke gehört werden, ist der kombinierte Ton doppelt so laut wie die einzelnen reinen Töne, wenn ihre Frequenzen weit auseinander liegen, und weniger laut als wenn ihre Frequenzen nahe beieinander liegen. Dies wird als Maskierungseffekt bezeichnet.
Der A-bewertete Schalldruckpegel ist eine Größe, deren Gewichtung an Reinton-Lautheitskurven angenähert ist. Damit stimmt der Parameter nicht mit der vom Menschen empfundenen Lautstärke für gewöhnlichen Lärm mit verschiedenen Frequenzen überein. Um eine Lautstärke zu bestimmen, die eher dem Gehörsinn entspricht, wurde daher eine Methode entwickelt und in ISO 532 standardisiert, die die Lautstärke von stationärem Rauschen unter Berücksichtigung des Maskierungseffekts berechnet. Diese Norm besteht aus ISO 532A von SS Stevens und ISO 532B von E. Zwicker . Ono Sokki verwendet ISO 532B. Bitte lesen Sie auch die nachfolgende Ergänzung.
(2) Gleichlautstärkekurve, Lautstärkepegel (Phon) und Lautstärke (Sone)
Abbildung 11.13 zeigt Reinton-Lautheitskurven (ISO 226:2003). Diese Zahl ist die gleiche wie die in Abschnitt 6-4 „Lautstärkepegel“ dargestellte; bitte beachten Sie auch die Beschreibungen dort.
Die Zahlen neben den Kurven geben die Lautstärkepegel an. Ein Phon entspricht dem Schalldruckpegel (dB) von 1 kHz Reinton. Eine Kurve gleicher Lautstärke ist eine Linie, die die Punkte des Schalldruckpegels bei verschiedenen Frequenzen verbindet, die dieselbe Hörlautstärke wie ein reiner Ton von 1 kHz haben. Dies ist eine A-Bewertung, angenähert an 40-Phon-Kurven mit gleicher Lautstärke. Lautheit ist jedoch keine psychologische Größe. Gewöhnliches 50-Phon-Geräusch klingt nicht doppelt so laut wie 40-Phon. Zwei gleichzeitig auftretende 40-Phon-Töne klingen nicht wie 50-Phon. Die Lautstärke eines reinen Tons (1 kHz) mit einem Schalldruckpegel von 40 dB wird hingegen als 1 Sone definiert. Die doppelte Lautstärke von 1 Sone wird als 2 Sone definiert.

Abbildung 11.13: Kurven gleicher Lautstärke des Reintons (ISO 226:2003)
So wie der Schalldruckpegel L p und der Geräuschpegel L A beide in dB angegeben werden, wird auch die Lautstärke umgerechnet und in dB angezeigt und phon als Maßeinheit für die Lautstärke verwendet. Die Beziehung zwischen Lautstärkepegel L (Phon) und Lautstärke S (Sone) kann mit der folgenden Gleichung ausgedrückt werden, solange L zwischen 40 und 120 Phon liegt.

Gleichung 11.9
Das bedeutet, dass jede Erhöhung des Lautstärkepegels um 10 Phon den Ton doppelt so laut macht (wenn S = 2 Sone, L = 50 Phon). Wenn S < 1, gilt die folgende Gleichung

Gleichung 11.10
(3) Kritische Bandbreite und Lautstärke
Das menschliche Ohr nimmt Geräusche je nach Frequenz an verschiedenen Stellen wahr. Das menschliche Ohr funktioniert wie ein Frequenzanalysator. Ein Band, das einer Bandbreite für die Frequenzanalyse entspricht, wird als kritisches Band bezeichnet. Es scheint, dass jedes kritische Band einen Maskierungseffekt hat. Beispielsweise erzeugt die Kombination von 250-Hz-Reinton und 1-kHz-Reinton einen Ton, der doppelt so laut ist wie diese Töne, wie im linken Teil von Abbildung 11-14 gezeigt. Andererseits erzeugt das Kombinieren von 250-Hz-Reinton und 500-Hz-Reinton keinen Ton, der doppelt so laut ist wie diese Töne. Das liegt an den kritischen Bändern, die dazu führen, dass der 250-Hz-Ton den 500-Hz-Ton maskiert.

Abbildung 11.14: Lautheit und Maskierung
Die Lautstärke des 250-Hz-Tons wird durch den schraffierten Bereich dargestellt. Die Lautstärke des 250-Hz-Tons und die des 500-Hz-Tons werden durch ihre schraffierten Flächen bestimmt. Der Bereich des 500-Hz-Tons, der durch den Bereich des 250-Hz-Tons maskiert (abgedeckt) wird, wird ausgeschlossen, wodurch der 500-Hz-Ton weniger laut wird als bei 1 kHz und näher an seiner Hörlautstärke. Wie durch den schraffierten Bereich des 250-Hz-Tons gezeigt, ist der Maskierungseffekt auf der niedrigeren Frequenzseite leicht (annähernd als vernachlässigbar) und auf der höheren Frequenzseite ausgeprägt. Ein weiteres Merkmal des Maskierungseffekts ist, dass je lauter der Ton, desto größer die Reichweite der Maskierung ist.
(4) Schärfe
Die Schärfe ist ein Maß für den Hochfrequenzgehalt eines Tons und wird als Verhältnis von Lautstärke mit Schwerpunkt auf Breitband zu normaler Lautstärke berechnet. Die Maßeinheit ist acum. Im Allgemeinen wird Lautheit mit überwältigender Kraft (laut, kraftvoll, stark usw.) assoziiert, während Schärfe mit etwas Metallischem (hart, nervig, kreischend) assoziiert wird.
(5) Beispiele für Messungen
Abbildung 11.15 zeigt Anzeigebeispiele für Loudness (Sone) und Loudness Level (Phon) anhand einer vereinfachten Messung unter Berücksichtigung des Maskierungseffekts.
Beispiel für die Anzeige auf Schallpegelmessern

Abbildung 11.15: Beispiel einer Lautheitsberechnung durch einen Schallpegelmesser
ISO 532B legt fest, dass die Lautheit auf der Grundlage einer FLAT-gewichteten 1/3-Oktav-Echtzeitanalyse bestimmt werden muss.
Die Lautstärke kann abhängig von der Umgebung, in der die Messungen durchgeführt werden, auf zwei Arten gemessen werden: in einem freien Schallfeld wie einem schalltoten Raum oder einem offenen Feld, in dem es keine Schallreflexion gibt; und in einem diffusen Schallfeld wie einer Turnhalle oder einem gewöhnlichen Raum, in dem Schall reflektiert wird. Diese Methoden verwenden unterschiedliche Berechnungen und ihre Messungen werden durch die Codes GF bzw. GD voneinander unterschieden.
Hinweis:
12. Berechnung von Dezi Bel (dB)
Nehmen wir an, wir haben zwei Schallquellen und ihre Schalldruckpegel sind L 1 (dB) bzw. L 2 (dB), wenn sie einzeln zu unterschiedlichen Zeiten Schall abgeben. Wenn nun diese Schallquellen Schall zum gleichen Zeitpunkt emittieren, ist der resultierende Schalldruckpegel nicht einfach gleich L 1 + L 2 . Um den Schalldruckpegel zu kennen, müssen wir ihre Dezibel summieren. In den folgenden Abschnitten werden grundlegende Methoden zur Berechnung von dB erläutert.
12.1 Summe der dB-Werte (Gesamtleistung)
Der kombinierte Schalldruckpegel L aus mehreren Schallquellen kann wie folgt bestimmt werden. Die Schalldruckpegel der Schallquellen L 1 , L 2 , ..... L n (dB) können aus dem Schalldruck an jeder Quelle p 1 , p 2 , ..... p n berechnet werden :

Gleichung 12.1
wobei p 0 der Referenzwert ist (p 0 = 20 μpa). Die obige Gleichung kann wie folgt in Exponentenschreibweise ausgedrückt werden.

Gleichung 12.2
Die Summe L davon in dB ist:

Gleichung 12.3
wobei L der kombinierte Schalldruckpegel ist. Beispielsweise können 80 dB und 70 dB wie folgt summiert werden.

Gleichung 12.4
Das Summieren von dB-Werten wird auch als Kombinieren von dB-Werten bezeichnet.
12.2 Durchschnitt der dB-Werte (Durchschnittsleistung)
Der Durchschnitt L der Summe von n dB-Werten kann bestimmt werden, indem die Gesamtleistung durch n dividiert wird und das Ergebnis dann wie folgt in dB logarithmiert wird.

Gleichung 12.5
wobei L die in Abschnitt 12-1 ermittelte Summe ist. Daher kann der Mittelwert durch Subtrahieren von 10 log 10 n von der Summe der dB-Werte erhalten werden. Beispielsweise kann die mittlere Leistung von 80 dB und 70 dB wie folgt berechnet werden.

Gleichung 12.6
12.3 Differenz der dB-Werte (Leistungsdifferenz)
Die Differenz L ' zwischen L 1 (dB) und L 2 (dB) kann wie folgt ausgedrückt werden.

Gleichung 12.7
Beispielsweise kann die Differenz zwischen 80 dB und 70 dB wie folgt berechnet werden.

Gleichung 12.8
Das obige Verfahren zur differentiellen dB-Berechnung kann zur Hintergrundgeräuschkorrektur bei der spezifischen Geräuschmessung verwendet werden. Sind der Schalldruckpegel L 1 (dB) inklusive spezifischem und Hintergrundgeräusch und der Schalldruckpegel L 2 (dB) (Hintergrundgeräusch) ohne spezifisches Geräusch bekannt, kann die Differenz bzw. der Pegel des spezifischen Geräusches berechnet werden.
12.4 Logarithmische Gleichung
Wie in Abschnitt 4.1 beschrieben, ist Dezi Bel (dB) das Zehnfache des Logarithmus zur Basis 10 des Verhältnisses einer physikalischen Größe (Leistung) zum Bezugsschalldruck. Das bedeutet, dass es wichtig ist, die logarithmische Rechnung zu verstehen. Hier sind einige der grundlegenden Eigenschaften des Logarithmus.
Grundlegende Eigenschaften
Die Zahl 1000 kann als 10 3 in Exponentenschreibweise ausgedrückt werden. Diese Beziehung kann mit Logarithmus zur Basis 10 als log 10 10 3 = 3 ausgedrückt werden. Im Allgemeinen gilt:

Gleichung 12.9
Der in der Lärmberechnung häufig verwendete Zusammenhang zwischen Antilogarithmus und Logarithmus wird im Folgenden skizziert.
Tabelle 12.1: Grundlegende logarithmische Gleichungen und Beispiele

12.5 Methode zur Berechnung des äquivalenten kontinuierlichen A-bewerteten Schalldruckpegels
ISO 1996 (JIS Z 8731) legt Verfahren zur Messung des äquivalenten kontinuierlichen A-bewerteten Schalldruckpegels fest, der zur Bewertung von Lärm in allgemeinen Umgebungen, Arbeitsumgebungen und unter anderen Bedingungen verwendet wird. Der äquivalente kontinuierliche A-bewertete Schalldruckpegel kann automatisch berechnet werden, indem Schallpegelmesser mit dieser spezifischen Berechnungsfunktion integriert werden. Aber selbst wenn Schallpegelmesser verwendet werden, die diese Funktion nicht haben, kann der äquivalente kontinuierliche A-bewertete Schalldruckpegel bestimmt werden, indem gemessene Schalldruckpegel (dB) gemittelt werden, wie unten gezeigt. Aus den in regelmäßigen Abständen gemessenen Schalldruckpegeln lässt sich der äquivalente A-bewertete Dauerschalldruckpegel L Aeq der Messzeitintervalle mit den folgenden Gleichungen ermitteln

Gleichung 12.10
wobei T das Messzeitintervall ist, n die Gesamtzahl der Messungen ist und L A1 , L A2 und L An gemessene Schalldruckpegel (dB) sind.
12.6 Methode zur Messung des Perzentil-Schalldruckpegels (50 Messungen)
Perzentiler Schalldruckpegel wird zur Messung und Bewertung von Schwankungsgeräuschen verwendet. Die folgenden Verfahren müssen befolgt werden, um prozentuale Schalldruckpegel zu erhalten. Stellen Sie zuerst die Zeitgewichtung auf Fast, nehmen Sie 50 Messungen in 5-Sekunden-Intervallen vor und notieren Sie die Messungen in der Reihenfolge, in der sie durchgeführt wurden, wie in Feld A von Tabelle 12.2. Zweitens sortieren Sie die Messungen basierend auf den Pegeln und geben Sie die Zwischensummen in eine Anzahl-von-Male-Tabelle wie Feld B von Tabelle 12-2 ein.
Während Messungen normalerweise mit der ersten Dezimalstelle angegeben werden, bestimmen Sie die zu verwendende Teilung der Skala entsprechend der erforderlichen Auflösung und zählen Sie die Messungen, die unter die gleiche Teilung fallen. Das unten gezeigte Beispiel verwendet zur Erleichterung der Erklärung und des Verständnisses eine 1-dB-Teilung. Geben Sie die Zwischensummen in eine Malzahltabelle ein, die in der Reihenfolge von niedrigen zu hohen Zahlen angeordnet ist, wie in Feld B von Tabelle 12-2, und geben Sie dann kumulative Zahlen in dieselbe Tabelle ein. Zeichnen Sie dann die Daten der Tabelle in einem Diagramm wie dem in Abbildung 12-1, in dem die Y-Achse kumulative Zahlen wie 1, 4 und 7 darstellt, während die X-Achse Schalldruckpegel wie 64,5, 65,5 und 66,5 darstellt. Zeichnen Sie eine glatte (Korrektur-)Kurve entlang der gezeichneten Punkte. Dies repräsentiert die Verteilung der kumulativen Messwerte. Ermitteln Sie anhand der Prozentskala und der Verteilungskurve den 95 %-Wert. Dies ist die ObergrenzeL 5 des 90 %-Bereichs. Ebenso ist der 50 %-Wert der Medianwert L 50 und der 5 %-Wert die untere Grenze L 95 der 90 %.

Tabelle 12.2: Beispiel für 50 Messungen zur Bestimmung des Perzentil-Schalldruckpegels

Abbildung 12.1: Perzentiler Schalldruckpegel und kumulative Verteilung
13. Referenzen und Nachweise
Im Folgenden sind einige der Normen und Literatur zu Geräuschmessung und Schallpegelmessern aufgeführt, die als Referenz zur Verfügung stehen.
Japanische Industriestandards (JIS)
| C 1509-1:2005 |
Schallpegelmesser – Teil 1: Spezifikationen |
| C 1502:1990 | Schallpegelmesser (bisherige Norm) |
| C 1505:1988 |
Präzisions-Schallpegelmesser (bisherige Norm) |
| C 1513:2002 |
Oktavband- und Terzband-Analysatoren für Geräusche und Schwingungen |
| C 1514:2002 |
Oktavband- und Teil-Oktavband-Filter |
| C 1515:2004 | Schallkalibratoren |
| C 5502-1991 | Mikrofone |
| C 5515-1981 |
Standard-Kondensatormikrofone |
| Z 8106:2000 |
Internationales elektrotechnisches Vokabular Kapitel 801: Akustik und Elektroakustik |
| Z 8731:1999 |
Beschreibung und Messung von Umgebungslärm |
| Z 8733:2000 |
Bestimmung der Schallleistungspegel von Geräuschquellen unter Verwendung von Schalldruck-Engineering-Methoden in einem im Wesentlichen freien Feld über einer reflektierenden Ebene |
| Z 8737-1:2000 |
Von Maschinen und Geräten emittierter Lärm-Messung des Emissions-Schalldruckpegels an einem Arbeitsplatz und an anderen festgelegten Stellen-Ingenieurverfahren in einem im Wesentlichen freien Feld über einer reflektierenden Ebene |
| X7778:2001 |
Deklarierte Geräuschemissionswerte von Computer- und Bürogeräten |
| X7779:2001 |
Messung von Luftschall, der von Geräten der Informationstechnik und Telekommunikation emittiert wird |
Normen der Internationalen Elektrotechnischen Kommission (IEC)
| 60942 |
"Schallkalibratoren" |
| 61043 |
„Elektroakustik – Instrumente zur Messung der Schallintensität – Messungen mit Paaren von Druckmessmikrofonen“ |
| 61094-1 | „Messmikrofone – Teil 1: Spezifikationen für Labor-Standardmikrofone“ |
| 61260 |
"Elektroakustik - Oktavband- und Bruchoktavbandfilter" |
| 61672-1 |
„Schallpegelmesser – Teil 1: Spezifikation“ |
Literatur
- Sakae Morita: Neue Ausgabe – Noise and Noise Abatement, Ohmsha
- Jun'ichi Saneyoshi: Electroacoustics, CORONA PUBLISHING
- The Acoustical Society of Japan: Noise and Vibration (Part 1/2), CORONA PUBLISHING
- The Japan Environmental Management Association for Industry: Industrial Pollution Control Technologies and Laws – Noise
- LE Kinsler und AR Frey: Grundlagen der Akustik, John Wiley & Sons, Inc.
- PM Morse: Vibration and Sound, McGraw-Hill Book Co., Inc.
- Ono Sokki Schallpegelmesser Technische Hinweise (Serien LA-200, LA-1200 und LA-5000)
Produktbroschüren
Ono Sokki Schallpegelmesser der Serien LA-3260/3560/3570 und LA-1400/
4400 und Vibrations-Echtzeit-Analysesystem DS-3000-Serie 'ESUFEEL'
Ono Sokki "OS-2000-Serie" "OC-1300-Serie"
Ono Sokki Co. Ltd. ist der alleinige Inhaber des Urheberrechts an diesem Handbuch. Jegliche Verwendung dieses Handbuchs zu anderen Zwecken als der persönlichen Referenz bedarf der vorherigen Genehmigung durch Ono Sokki Co., Ltd.

