Informationen
Dämpfungsmaterialien
Inhaltsverzeichnis
4. Messmethode für die Dämpfungsleistung
6. Decay-Ratio-Methode/ Zerfallsverhältnismethode
9. Standard für Dämpfungsleistungsmessung
10. Testmethode für die Dämpfungsleistung
11. Cantilever-Methode
11.1. Die Wahl des Musters
11.2. Das Blockdiagramm der Cantilever-Methode
11.3. Die Genauigkeit der Verlustfaktormessung mit der Cantilever-Methode
11.4. Notizen
11.5. Auswahl des Gerätes für das Cantilever-Verfahren
12. Central Exciting-Methode
12.1 Merkmale der zentralen Anregungsmethode
12.2 Impedanzkopf
12.3 Resonanz, Anti-Resonanz für die Central Exciting-Methode
12.4 Fehlerursachen
13. Methodenauswahl (Cantilever-Methode und Central-Springing-Methode)
14. Vergleiche von Verlustfaktoren, die mit verschiedenen Methoden erhalten wurden
16. Notwendigkeit der FFT-Zoomanalyse
17. Zoom-Analyse und Massenlöschung
18. Kurvenanpassung durch Verwendung von Pol-Null-Modellen für die Verlustfaktormessung
18.1 Einleitung
18.2 Die Pole-Null-Modelle
18.3 Fehlerunktion für die Kurvenanpassung
18.4 Antrag auf Modelldaten
18.5 Tatsächliche Messung mit der Kurvenanpassungsmethode
19. Hängende Methode mit zwei Punkten
20. Der Verlustfaktor hängt vom Vibrationsmodus ab
21. Um eine genaue Frequenzgangfunktion zu erhalten
21.1 Sweep-Sinussignal
21.2 Mehrere Sinussignale
21.3 Impulssynthese
21.4 Zufallssignal
22. Window-Funktion zur Messung des Verlustfaktors
23. Berechnung des Elastizitätsmoduls
23.1 Reines Material
23.2 Die laminierten Verbundplatten
23.3 Die Verbundplatten mit Sockel zwischen den Dämpfungsmaterialien
23.4 Schubmodul und Verlustfaktor für die Verbundplatten mit dem Dämpfungsmaterial zwischen Tragschicht und Zwangsschicht
24. Physikalische Eigenschaft von viskoelastischen Materialien
24.1Temperatur-Frequenz-Überlagerung
24.2 WLF-Gleichung
25. Nomogramm der reduzierten Frequenz
25.1 Erstellen des reduzierten Frequenznomogramms
25.2 Verfahren zum Erstellen von Nomogrammen
25.3 Hinweise zum Erstellen von Nomogrammen
25.4 So lesen Sie das Nomogramm der reduzierten Frequenz
27. Näherung des Verlustfaktors
28. Näherung des Elastizitätsmoduls
29. Messung des Verlustfaktors für die Verformung von Dämpfungslegierungen
31. Ergänzungsmerkmale des elektromagnetischen Erregers (Detektor), der für die Cantilever-Methode verwendet wird
31.1 Impedanzcharakteristik des elektromagnetischen Detektors
31.2 Die Messung der Schwingungsgeschwindigkeitsantwort und Linearität für elektromagnetische Detektoren
31.3 Die Vibrationsgeschwindigkeitsantwort und Linearität für elektromagnetische Detektoren
31.4 Fazit
Im Bereich der Schwingungsmessung und -analyse gibt es Begriffe wie „Dämpfung“ und „Dämpfungsmaterialien“. Die Dämpfung dient dazu, die Schärfe der Vibration zu steuern, um Vibrationsenergie in thermische Energie umzuwandeln; Es ist ein völlig anderer Ansatz als die „Vibrationsisolierung“, die eine Hauptmethode ist und durch Änderung der Steifigkeit, Vibrationsisolierung zur Reduzierung von Vibrationen gesteuert wird. Die Dämpfung versucht, Vibrationen so weit wie möglich zu reduzieren und eine angenehmere Umgebung zu schaffen. Wir konzentrieren uns auf „Dämpfung“ in Bezug auf Bedeutung und Unterschiede, erklären, wie Dämpfungsmaterialien gemessen werden, und greifen einige wichtige Punkte für die Messung auf. Wir empfehlen besonders denjenigen, die sich mit Dämpfung und Schwingungsisolierung beschäftigen, diesen Bericht durchzulesen.
1. Dämpfung
„Dämpfung“ reduziert das Vibrationsniveau auf der Oberfläche eines Festkörpers, um Vibrationsenergie in Wärmeenergie umzuwandeln, während „Vibrationsisolierung“ der Vibrationsisolierung entspricht, um die Vibrationsübertragungsrate zwischen Vibrationsquelle und vibrationsempfangendem Gerät zu reduzieren. Es muss zwischen Dämpfung und Schwingungsisolierung unterschieden werden. Die Dämpfung ist nicht nur in der Lage, Vibrationen selbst zu reduzieren, sondern auch Geräusche zu reduzieren, und zeigt besonders Wirkung bei der Reduzierung von Vibrationen in der Nähe des Resonanzpunktes. Die Dämpfungstechnologie wurde lange Zeit für die Messung von Schwingungen untersucht, während Dämpfungsmaterialien aktiver untersucht und entwickelt wurden, um die Technologie für Gegenmaßnahmen gegen Lärm anzuwenden.
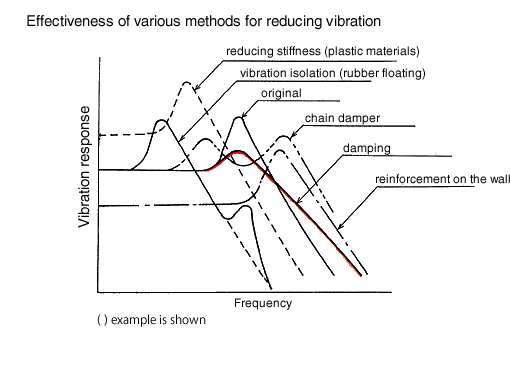
2. Dämpfungsmaterialien
Dämpfungsmaterialien sind zusammengeklebte Grundmaterialien (Stahl, Holz, Beton, Kunststoffe usw.) und viskoelastische Materialien (Harz, Gummi, Metall usw.). Es gibt den uneingeschränkten Typ (Basis + Dämpfungsmaterialien) und den eingeschränkten Typ (Basis + Dämpfungsmaterialien + Bindematerialien). Dämpfungsmaterialien (mit Klebebändern) werden als uneingeschränkte Art verkauft. Vibrationsstahlplatten werden als Zwangstyp verkauft.
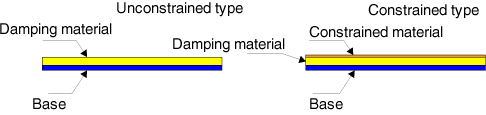
3. Verlustfaktor
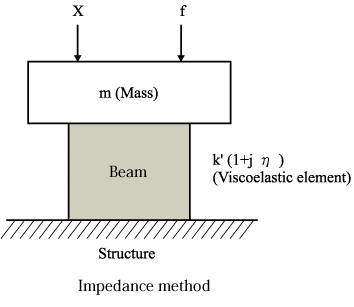
Der Verlustfaktor η ist ein Leistungsindex zur Messung von Dämpfungsmaterialien. Wenn die Schwingungsantwort gedämpft wird, stellt ihre Spannung/Verformung (oder Last/Verschiebung) eine Hysteresekurve dar, die durch den Verlustfaktor η = K 2 / K 1 berechnet wird, indem f = K 1 X bei der maximalen Verschiebung und f = K 2 Χ gemessen wird bei der Nullverschiebung. Wenn K1 für eine reelle Zahl steht, steht K 2 für eine imaginäre Zahl wie in Abb. 2, K' ist ein komplexer Elastizitätsmodul, K 2 ist ein Speichermodul, K 2 ist ein Verlustmodul.
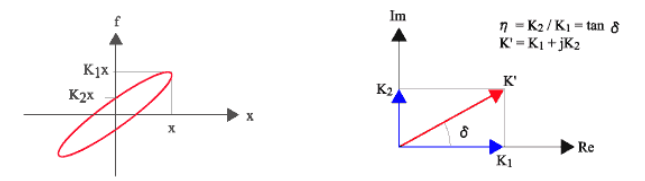
Abbildung 1 und 2
Obwohl es verschiedene Werte gibt, um die Dämpfungsleistung nach elektrischem, mechanischem und physikalischem Bereich anzugeben, sind hier die Beziehungen zwischen den einzelnen Werten aufgeführt.
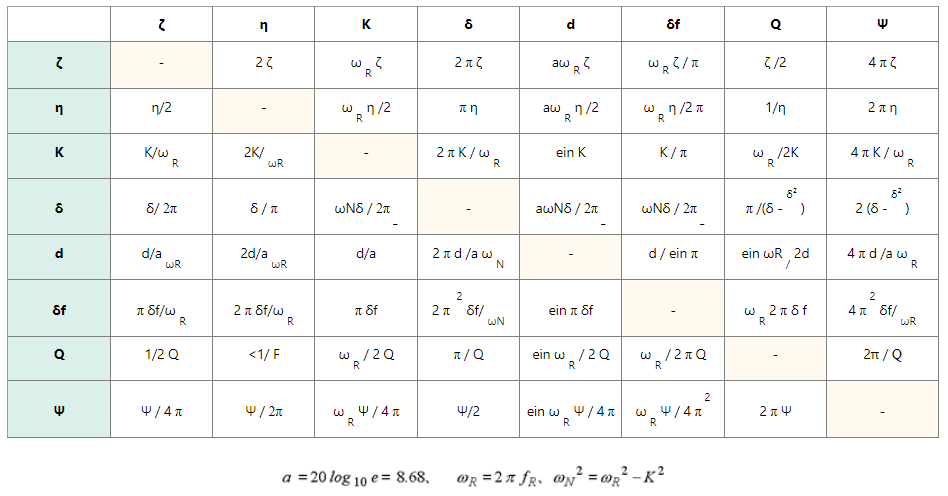
Tabelle 1
| : | Dämpfungsverhältnis, Verhältnis Viskositätskoeffizient : kritische Viskositätskonstante der Dämpfung = 2 √km |
| : | Verlustfaktor, k(1+iη) stellt elastische Elemente dar, einschließlich Feder- und viskoser Widerstand als komplexe Notation |
| K: | Dämpfungskonstante, Vibrationsdämpfung von |
| : | Logarithmus-Dämpfungsverhältnis, falls sich die Schwingungsamplitude abschwächt, angrenzendes Amplitudenverhältnis gegen natürlichen Logarithmus |
| d : | Dämpfungsgrad, Vibrationsdämpfung entspricht Dämpfungswert pro 1 Sek. in dBNachhallzeit (Zeit, um das Signal auf 60 dB zu reduzieren) T = 60/d |
| δf: | Halbbandbreite, die die Frequenz in der Nähe des Resonanzpunkts darstellt . Die Frequenzbreite entspricht 1 / √2 der maximalen Resonanzkurve |
| Q : | die Resonanzschärfe entspricht dem 2 π-fachen der Energie des Vibrationssystems und der Energie pro Zyklus, die von außen bereitgestellt wird, um die Vibration aufrechtzuerhalten |
| : | Spezifische Dämpfungskapazität, Verhältnis Verlustenergie pro 1 Zyklus : Energiegewinn am Vibrationssystem |
4. Messmethode für die Dämpfungsleistung
Der Verlustfaktor η ist die beliebteste Methode für den Leistungsindex der Dämpfung. Die klassischen Methoden (Resonanzmethoden) sind die Halbwertsmethode, die Dämpfungsmethode und die mechanische Impedanzmethode, während die Nicht-Resonanzmethode als nicht üblich gilt.
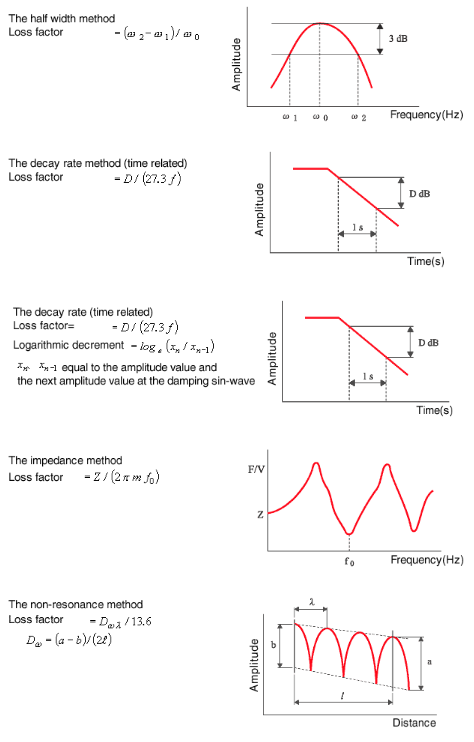
5. Halbwertsverfahren
Wenn X: Verschiebung, k: dynamische Federkonstante, c: viskoser Dämpfungskoeffizient, m: Masse, 1 Freiheitsgrad der Frequenzgangfunktion H (jΩ) vibriert durch externe Kraft F ist wie folgt: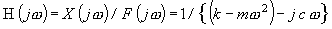
Wann|H| 2 max : Maximalwert der Amplitude für die Frequenzgangfunktion, Ω 0 : Kreisfrequenz, Ω 1 , Ω 2 : Schwingungsfrequenz am Punkt der Hälfte von |H| 2 max nahe Ω 0 ist der Verlustfaktor wie folgt: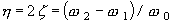
Bei tatsächlichen Tests ist es üblich, die Dämpfungsleistung gemäß der Resonanzfrequenz f 0 zu erhalten, um die Frequenz f 1 , f 2 abzulesen , die weniger als 3 dB vom Spitzenwert der Frequenzantwortfunktion entfernt ist.
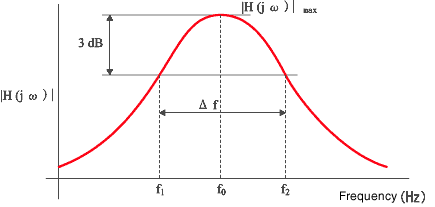
Es ist eine nützliche Berechnung als
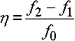
Es ist eine Berechnung ohne f 0 als
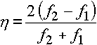
*Manchmal wird die n-dB-Methode anstelle der Halbwertmethode verwendet. Der Korrekturwert ist K wie folgt:
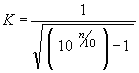
K= 1,9652 bei 1 dB, K= 1,3076 bei 2 dB
*Verlustfaktor, erhalten aus der Halbwertsmethode unter Verwendung der imaginären Zahl der Frequenzgangfunktion
Sie errechnet sich nach obiger Rechnung (η = K( f 2 - f 1 )/f 0 ) nach dem Halbwert (1/2 nicht 1/√21) der imaginären Zahl für die scheinbare Masse (Kraft/Beschleunigung). ). Wenn alle imaginären Zahlen von F/a „minus“ sind und der untere Wert –X ist, um bei der FFT Beschleunigung in CH A und Kraft in CH B einzugeben, werden f 1 , f 2 durch den folgenden Wert berechnet (wenn das Signal umgekehrt eingegeben wird , beide imaginären Zahlen stimmen nicht überein):
| Korrekturwert | |
| -X/1,259 (A= 1dB) | K = 1,965 |
| -X/1,585 (A= 2dB) | K = 1,308 |
| -X/2 (A= 3dB) | K = 1.000 |
(Es ist derselbe Korrekturwert wie MAG der Frequenzgangfunktion)
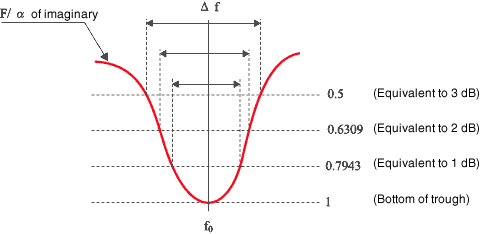
*Verlustfaktor, erhalten durch die Halbwertsmethode unter Verwendung der reellen Zahl der Frequenzgangfunktion
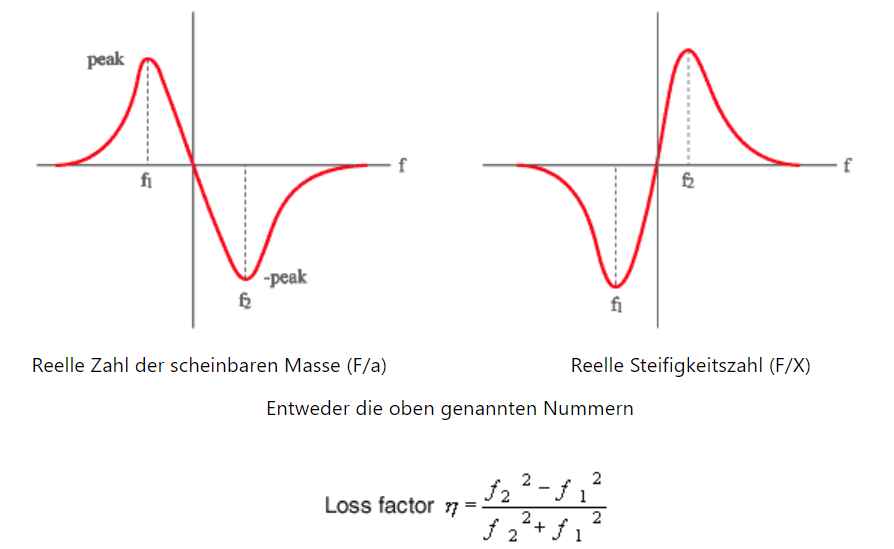
6. Decay-Ratio-Methode/ Zerfallsverhältnismethode
Beeinflusst durch die äußere Kraft, erzeugt das System mit 1 Freiheitsgrad stationäre Schwingungen. Ohne die äußere Kraft wird die Schwingung gedämpft, was die Hüllkurve der Schwingungsamplitude darstellt
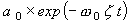
d (dB / sec), a 0 ist eine feste Zahl gemäß der Anfangsbedingung. Die Dämpfung d (dB/sec) für diese Hüllkurve ist wie
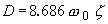
Der Verlustfaktor wird berechnet als
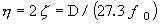
*Ω 0 = 2 πf0
Der Verlustfaktor wird auch berechnet, um T 60 zu messen (Zeit zum Dämpfen von Vibrationen auf 60 dB).
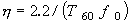
Es wird als Nachhallzeitmethode bezeichnet. Diese Verfahren werden für kleine Dämpfungen verwendet. Um die dämpfende Vibrationswelle durch einen logarithmischen Verstärker, wie z. B. einen Pegelschreiber, anzuzeigen, kann sie als gerade Linie im Verhältnis zur Hüllkurve dargestellt werden. Das Zerfallsverhältnis wird durch die Steigung der geraden Linie berechnet. Die Hilbert-Transformation ermöglicht es, das Abklingverhältnis zu erhalten.
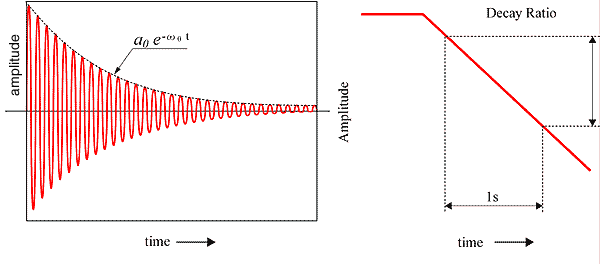
Die Steigung der geraden Linie sollte nicht rechts nach Beginn der Dämpfung oder an dem Punkt nahe dem festen Wert der Dämpfungsschwingungswelle übernommen werden. Falls es aufgrund des niedrigeren Vibrationsmodus keine klare gerade Linie gibt, findet die Filterung statt. Wenn die Amplitude χ n , χ n+1 unter der dämpfenden Sinuswelle liegt, wird der natürliche logarithmische Wert als logarithmisches Dekrement bezeichnet, das die Dämpfungskapazität von metallischem Material darstellt.
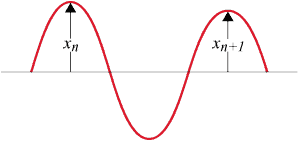
7. Impedanzmethode
Die Impedanzmethode ist nützlich für die Messung des Verlustfaktors bei großer Dämpfung. Die Amplitude für das Euter-1-Freiheitsgradsystem der mechanischen Impedanz (F/V) als |z|, |z| = c gemäß 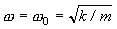 , die Impedanz repräsentiert den viskosen Dämpfungskoeffizienten. V bedeutet Schwinggeschwindigkeit. Daher wird der Verlustfaktor berechnet als
, die Impedanz repräsentiert den viskosen Dämpfungskoeffizienten. V bedeutet Schwinggeschwindigkeit. Daher wird der Verlustfaktor berechnet als
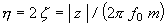
Genau genommen berechnet sich die Masse m durch μ∫W i 2 dx ( μ gleich Masse pro Längeneinheit, W i gleich Kriteriumsfunktion unter i-fachem Schwingungsmodus). Der Verlustfaktor kann auch durch mechanische Nachgiebigkeit berechnet werden. Wenn ein System mit 1 Freiheitsgrad durch Kraft in Schwingung versetzt wird (f = f 0 e jwt ), stellt die Nachgiebigkeit die Feder dar als g(1+ η j)
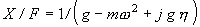
Der Realteil als R, der Imaginärteil als I, g und η wird berechnet als
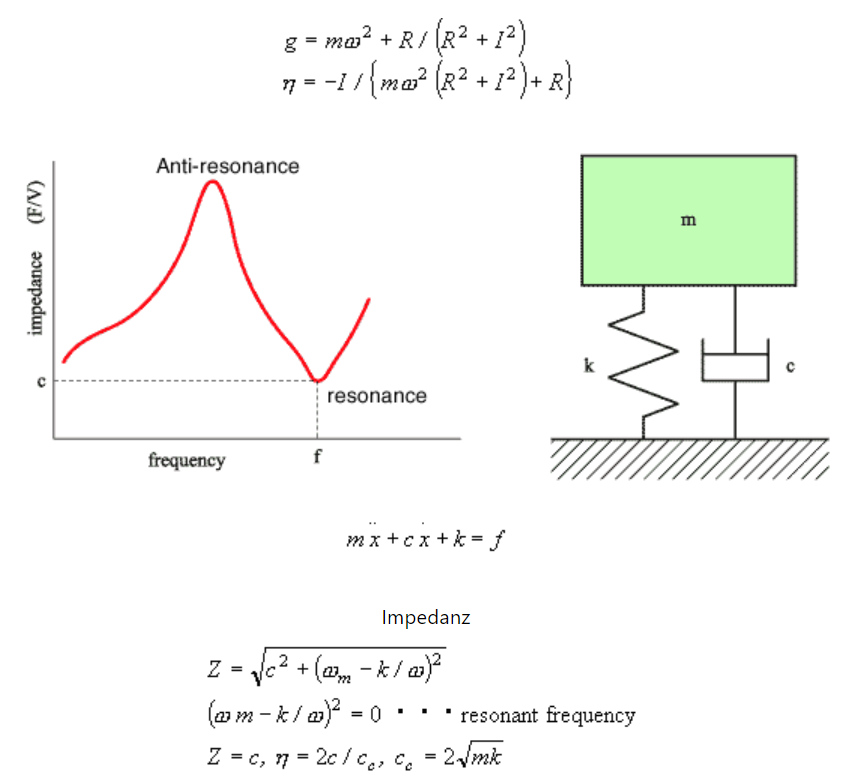
Die tatsächliche Berechnung wie folgt
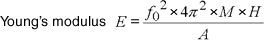
f 0 : Resonanzfrequenz (Hx)
M : Probengewicht + Obergrenze des Gewichts (kg)
h : Probendicke (m)
A : Probenfläche (m 2 )
E : Elastizitätsmodul (N/m 2 )
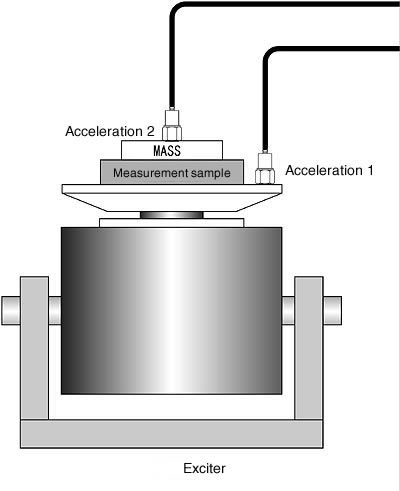
Der Verlustfaktor wird nach der Halbwertmethode unter Verwendung des Verhältnisses Beschleunigungssensor 1 : 2 wie oben berechnet.
8. Nicht-Resonanz-Methode
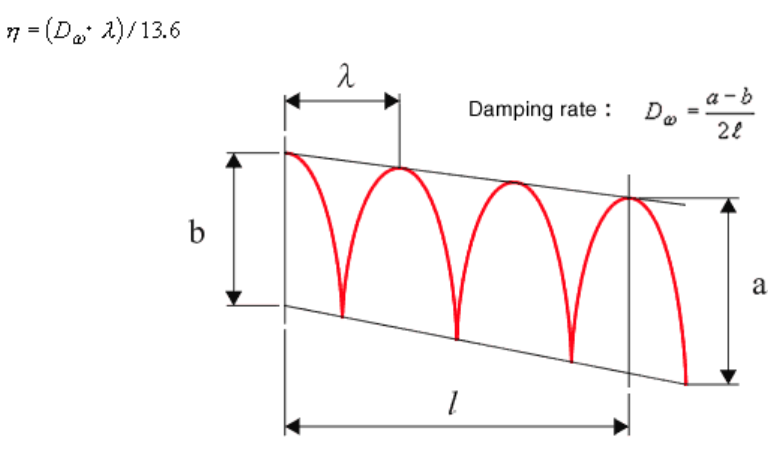
Die Halbwertmethode und die Zerfallsverhältnismethode sind Resonanzmethoden, bei denen der Verlustfaktor am oder in der Nähe des Resonanzpunktes gemessen wird. Während das Verfahren hier durch beliebige Frequenz gemessen wird. Die Kante des langen Balkens ist im Sand vergraben, die andere Kante wird durch einen Shaker vibriert. Dann wird der Verlustfaktor aus der Wellenlänge λ (m) der auf dem Balken auftretenden stehenden Welle oder Wanderwelle und der Schwingungsdämpfung d (dB/m) berechnet.
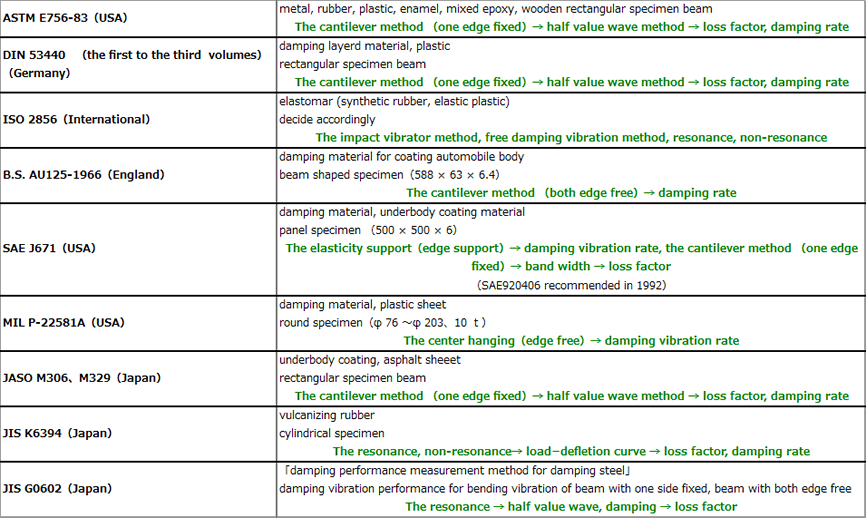
9. Standard zur Messung der Dämpfungsleistung
In Japan gibt es gängige Standards wie JIS K6394, JASO M306, M329m, während ASTM E756, BS AU125, DIN 53440, MIL P22581, SAE J671 weltweit und ISO 2856 als internationaler Standard gelten. Kürzlich wurde SAE 1992, USA, teilweise überarbeitet, JIS G0602 für den laminierten Dämpfungsstahl wurde 1994, Japan, hinzugefügt. In diesen Normen werden verschiedene Methoden zur Bewertung der Dämpfungsleistung vorgeschlagen und/oder empfohlen. Die Cantilever-Methode ist eine der beliebtesten Methoden und wird von ASTM, dIN und JASO übernommen. Dies ist die Methode, bei der ein langer, schmaler rechteckiger Probenbalken verwendet wird, der die Halbwertsbreite misst, um die Dämpfungsleistung zu bewerten. Die Zweipunkt-Stützmethode wird in BS angepasst, wobei das Schwingungsdämpfungsverhältnis an beiden Kanten des kurzen Probenbalkens gemessen wird, der von einer Messerschneide gestützt wird. Das Vibrationsdämpfungsverhältnis wird gemessen, indem die Probenplatte mit der Stoßanregung und/oder Einzelfrequenzanregung vibriert, die in MIL, SAE angepasst ist. Die Impedanzmethode ist die beliebteste in Japan, bei der die Mitte des Probenbalkens durch Sinuswellenerregung und/oder zufällige Erregung in Schwingung versetzt wird und die Impedanz am Antriebspunkt gemessen wird, um die Dämpfungsleistung zu bewerten. Anders als oben gibt es Testgeräte, die verkauft werden, um die Dämpfungsleistung mit dem Entlastungsphänomen zu bewerten, das durch viskoelastisches Material dargestellt wird. Der Messfrequenzbereich dieser Geräte beträgt jedoch hunderte von Hz. bei dem die Mitte des Probenbalkens durch Sinuswellenanregung und/oder zufällige Anregung in Schwingung versetzt wird und die Impedanz am Antriebspunkt gemessen wird, um die Dämpfungsleistung zu bewerten. Anders als oben gibt es Testgeräte, die verkauft werden, um die Dämpfungsleistung mit dem Entlastungsphänomen zu bewerten, das durch viskoelastisches Material dargestellt wird. Der Messfrequenzbereich dieser Geräte beträgt jedoch hunderte von Hz. bei dem die Mitte des Probenbalkens durch Sinuswellenanregung und/oder zufällige Anregung in Schwingung versetzt wird und die Impedanz am Antriebspunkt gemessen wird, um die Dämpfungsleistung zu bewerten. Anders als oben gibt es Testgeräte, die verkauft werden, um die Dämpfungsleistung mit dem Entlastungsphänomen zu bewerten, das durch viskoelastisches Material dargestellt wird. Der Messfrequenzbereich dieser Geräte beträgt jedoch hunderte von Hz.
10. Testverfahren für die Dämpfungsleistung
Die gängigen Verlustfaktor-Prüfmethoden sind der Cantilever, der zentrale Spanner, die Zwei-Punkt-Aufhängung und die Zwei-Punkt-Abstützung. Üblicherweise werden für diese Prüfungen der Oberst-Balken und/oder der Sandwich-Balken verwendet. Das Folgende zeigt die allgemeinen Eigenschaften, das Testsystem, den Fehlerfaktor und das Testergebnis des Verlustfaktors für den Cantilever und die zentrale Anregungsmethode.
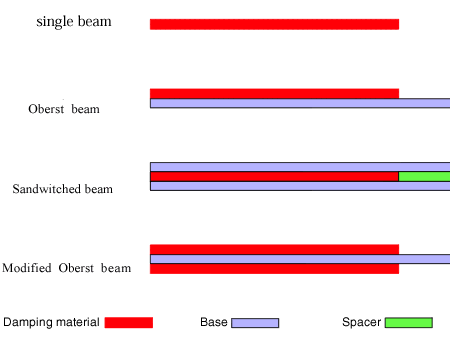
Die Eigenschaften der Probe
| Oberst Strahl | einfach zu machen Probendaten sind tendenziell stabil |
| Sandwich-Strahl | Schwierig, Proben zu machen, muss Spaer- Resonanzfrequenz tendenziell nicht stabil sein |
| Modifizierter Oberst-Balken | schwierig zu machen Probe (Fehler auf Probe) Daten neigen dazu, nicht stabil zu sein |
11. Cantilever-Methode
Dieses Verfahren ist in dIN, ASTM, JASO, JIS und das Prüfverfahren in SAE angepasst.
11.1 Die Wahl des Musters
Normalerweise wird anhand des Elastizitätsmoduls entschieden, welcher Probentyp verwendet wird. Es ist nicht in der Lage, die Beziehung zwischen dem Elastizitätsmodul des Dämpfungsmaterials und dem messbaren Frequenzband eindeutig zu bestimmen. Die allgemeine Beziehung ist wie folgt:
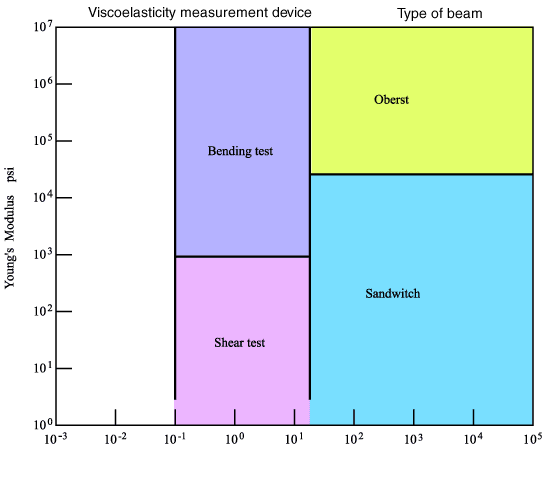
11.2 Das Blockdiagramm der Cantilever-Methode
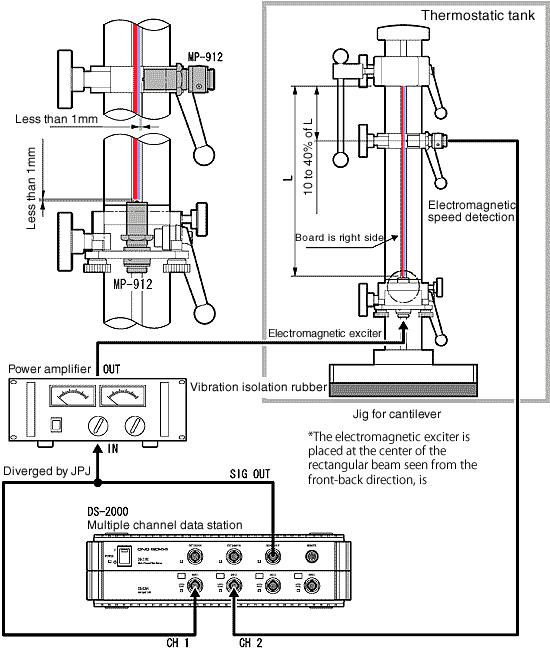
11.3 Die Genauigkeit der Verlustfaktormessung mit der Cantilever-Methode
Die Messung des Verlustfaktors ist ein ziemlich empfindlicher Test. Auch bei sorgfältiger Herstellung der Probe können der Verlustfaktor und/oder die Resonanzfrequenz variieren. Dies wird durch geringfügige Unterschiede in den Eigenschaften des Dämpfungsmaterials und des Balkens sowie durch Fehler bei der Herstellung von Proben verursacht. Um diese Fehler zu vermeiden, ist es effektiv, den Durchschnittswert des Verlustfaktors und der Resonanzfrequenz unter Verwendung von 3 oder mehr Proben zu erhalten. Die folgende Abbildung zeigt die Änderungen des Verlustfaktors im Laufe der Zeit. Wie gezeigt, ist der Verlustfaktor am Punkt der Temperaturänderung nicht stabil, 2 Stunden später wird dieses Dämpfungsmaterial stabil. Die andere Abbildung unten zeigt den Verlustfaktor und die Temperatur, den Verlustfaktor und die Resonanzfrequenz mit der Cantilever-Methode.
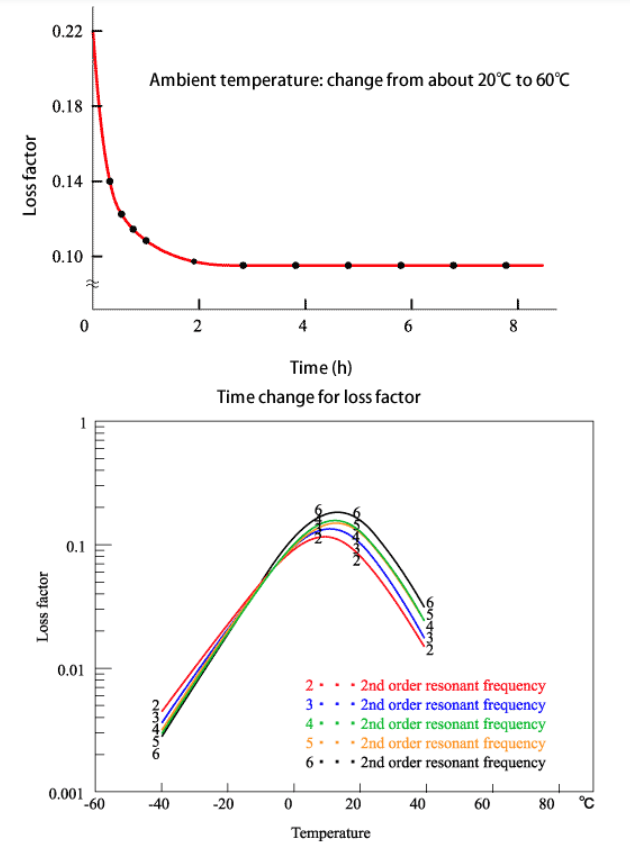
11.4 Notizen
| 1 | Das Aspektverhältnis für die Probenabmessung ist 20:1 wünschenswert. |
| 2 | Schlechte Haftung aufgrund der Luftmischung auf der Klebefläche.Die Dicke des Klebematerials beträgt weniger als 0,05 mm, der Elastizitätsmodul ist 10-mal höher als bei Dämpfungsmaterial. |
| 3 | defektes Exemplar. Maßgenauigkeit. Ungleichmäßige Dicke.Es wird nur eine Biegeschwingung benötigt. |
| 4 | Loses Befestigungsende. Gleiten. Die zunehmende Dämpfung aufgrund von Reibungsverlust, loser Befestigung und nichtlinearen Phänomenen wirkt sich am stärksten auf den ersten Schwingungsmodus aus.Daher ist es besser, die ersten Resonanzdaten nicht anzupassen. Das Befestigungsende sollte fest befestigt sein. |
| 5 | Temperaturkontrolle. Probe bei gleicher Temperatur belassen. Justieren Sie innerhalb von ±1℃. |
| 6 | Fehler der Resonanzfrequenz. Angemessene überstrichene Geschwindigkeit.Die Frequenz benötigt eine Genauigkeit von ±1 %, da sie quadratisch wirkt, wenn der Elastizitätsmodul berechnet wird. Die Vibration sollte nicht innerhalb eines nichtlinearen Bereichs hinzugefügt werden. (insbesondere Einzelbrett) (Linerbereich: Schwingungsamplitude proportional zu periodischer Belastung und Dehnung) |
| 7 | Fehler der DämpfungDer Modus ist nicht geschlossen. Keine Dämpfung der Befestigungskante wirkt. Dämpfung durch Non-Liner vermeiden. |
| 8 | Rechenfehler |
| 9 | Einstellung von Empfänger, Exciter.Der Abstand zwischen elektromagnetischem Empfänger und elektromagnetischem Erreger beträgt mehr als 80 mm, um ein durch elektromagnetische Streuung verursachtes Übersprechen zu vermeiden. |
| 10 | Beeinflussung der FrequenzauflösungDie wünschenswerte Anzahl von Messpunkten innerhalb der Halbwertsbreite beträgt mehr als 20. |
11.5 Die Wahl des Gerätes für das Cantilever-Verfahren
Berührungsloser elektromagnetischer Erreger
Die Struktur des berührungslosen elektromagnetischen Erregers, der hauptsächlich für die Cantilever-Methode verwendet wird, wie folgt:
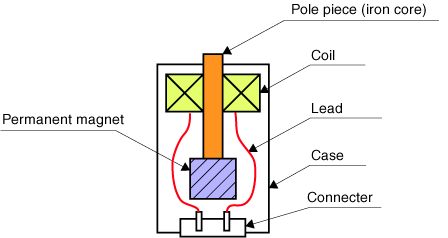
Es ist besser, eine dickere Spule (ca. Φ0,1 mm) etwa 1000 Mal aufzuwickeln. Es hat keinen Sinn, mehr aufzuwickeln, da es aufgrund des zunehmenden Gleichstromwiderstands und der Reaktanz nicht in der Lage ist, mit hoher Frequenz zu schwingen. Es ist eine Anleitung zum Aufwickeln von Spulen mit 100-Ω-dC-Widerständen, wenn der Audioverstärker auf dem Markt verwendet wird. In diesem Fall beträgt die Reaktanz 20 mH. Der Permanentmagnet wird unter dem maximalen Wert des magnetischen Wechselfeldes des elektromagnetischen Erregers verwendet. Falls der berührungslose elektromagnetische Erreger mit voller Leistung verwendet wird, reicht das Gleichstromfeld möglicherweise nicht aus. In einem anderen Fall wird die kleine, leichte Probe vibriert; DC-Feld könnte zu stark sein. Der Permanentmagnet wird jeweils als Elektromagnet verwendet (um die Spule wieder aufzuwickeln), dann liegt Gleichspannung an.
Berührungsloser elektromagnetischer Sensor
Der Aufbau ist genau derselbe wie beim berührungslosen elektromagnetischen Erreger. Die gleiche Anzahl von Windungen, Walzdrähte wird empfohlen. Falls das Signal anstelle des Verstärkers an den FFT-Analysator gesendet wird, ist die kleinere Ausgangsimpedanz wünschenswert. Es hat keinen Sinn, schmalen Draht viele Male aufzuwickeln. Die Ausgabe dieses Sensors ist proportional zur Geschwindigkeit, und es ist einfach, diesen Sensor zu verwenden, da er Hochfrequenz messen kann. In seltenen Fällen stört es nicht berührbare elektromagnetische Erreger, daher ist darauf zu achten, dass es in unmittelbarer Nähe zu nicht berührbaren elektromagnetischen Erregern verwendet wird.
Kapazitätssensor
Das Betriebsprinzip ist wie folgt:
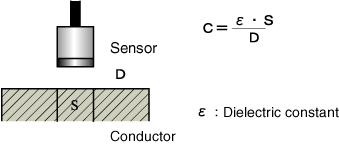
Die Genauigkeit zwischen Sensor und Ziel ist mit 0,1 % sehr gut. Das Verhältnis der sensitiven Entfernung zwischen Sensordurchmesser und Messobjekt beträgt jedoch 10:1. Das Ziel sind Ferroelektrika. Es hat den Nachteil, Hochfrequenz als Wegsensor zu messen, während es den Vorteil hat, nicht mit berührungslosen elektromagnetischen Erregern zu interferieren.
Beschleunigungssensor
Am beliebtesten ist der Beschleunigungssensor vom piezoelektrischen Typ. Besonders wenn Hochfrequenz gemessen werden muss, ist der Beschleunigungssensor vom piezoelektrischen Typ derzeit der beste. Er ist unter anderen Vibrationssensoren am einfachsten zu verwenden, manchmal ist jedoch sein Gewicht ein Problem. Bei der Messung des Verlustfaktors, des Elastizitätsmoduls, ist ein Gewichtsverhältnis von 100:1 oder weniger wünschenswert. Achten Sie auch darauf, dass das Anschlusskabel nicht dämpft. Außerdem können die Klebstoffe eine Resonanz verursachen. Die kleinen Sensoren haben eine geringe Empfindlichkeit und können das S/N-Verhältnis verschlechtern. Der elektrische Ladungsempfindlichkeitstyp ist 1 pC/ms –2 oder mehr, der elektrische Spannungsempfindlichkeitstyp ist 1 mV/ms –2 bevorzugt.
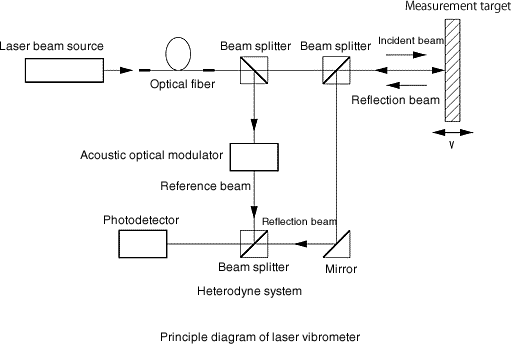
Laservibrometer
Es ist der beste Reaktionssensor. Der Abstand zwischen Ziel und Sensor beträgt mehr als 100 mm, die Verschiebungsgenauigkeit beträgt 10 -11 m, die Frequenz mehr als 1 MHz. Es sei denn, das Ziel hat eine perfekte Reflexion, ist transparent und kann mit beliebigen Materialien gemessen werden. Es wird am häufigsten als Antwortsensor für die Cantilever-Methode verwendet. Auch wird er als Beschleunigungssensor mit Impedanzkopf für das zentrale Anregungsverfahren verwendet. Das Messprinzip besteht darin, die relative Geschwindigkeit des Sensors/Ziels zu messen, wodurch der Sensor fest auf der stabilen Platte befestigt ist. Falls es in einem Thermostattank verwendet wird, ist darauf zu achten, die obere Grenztemperatur und plötzliche Temperaturänderungen zu kontrollieren, um Kondensation zu verursachen. Ein weiterer Nachteil sind die hohen Kosten.
12. Central Exciting-Methode
Diese Methode wird als mechanische Impedanz bezeichnet und im JIS-Standard für die Dämpfungsstahlplatte übernommen, wie erwähnt, aber in Europa und den USA nicht verbreitet. Das folgende Diagramm zeigt ein beliebtes Messsystem des Verlustfaktors nach der zentralen Anregungsmethode sowie der Cantilever-Methode.
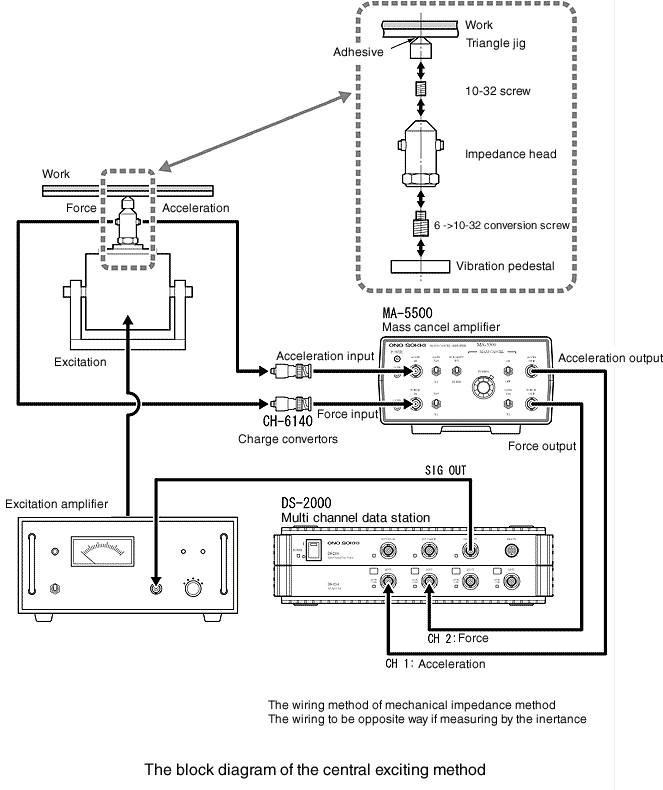
In den USA ist die Impedanzmethode die Messung des Verlustfaktors mit der Impedanz, um einen Block aus Dämpfungsmaterial zu verwenden.
Kürzlich wurde die zentrale Erregung in SAE 920406 eingeführt.
12.1 Merkmale der zentralen Anregungsmethode
*Vorteil
- Messung der Hochfrequenzbänder möglich
- Flexiblere Probenabmessungen
* Nachteil
- Kompliziertes Gerät
- Unsichere Auswirkung des Stützpunktes
* Probe
- Rechteck, Blockform
* Testverfahren
- Sinuswelle oder zufällige Vibration, langsamer Sweep mit Sinuswelle
- Die Antwort kann mit Frequenzganganalysator, FFT-Analysator und Pegelschreiber aufgezeichnet werden. Achten Sie auf Frequenzauflösung, Trunkierung und Lesefehler.
* Annahme, Anmerkungen
- Es ist wünschenswert, dass die Probenabmessung ein Aspektverhältnis von 20:1 oder höher aufweist.
- Die Prüfung erfolgt innerhalb linearer. Achten Sie darauf, die Schwingungsamplitude zu überwachen. Es ist nur eine schöne Vibration, die man sehen kann oder nicht.
- Erregerkraft stabil sein.
- Die Biegeanregung wird nicht zur Torsionsanregung.
- Die Messung ist in der Nähe des Resonanzfrequenzpunkts à innerhalb von fc / 10
durchzuführen. Innerhalb der Halbwertsbreite sind 20 oder mehr Messpunkte wünschenswert. - Die ideale Klebstoffbreite der Messerkante ist Null oder wünschenswert für 1/200 oder weniger der Probenlänge (0,5 mm oder weniger gegenüber 100 mm Probe)
- Massenlöschung für WägezelleMit oder ohne Massenentwertung wird mit 0,03 und weniger Verlustfaktor der Probe beeinflußt
- Durchzuführende Zoom-Analyse
Mit oder ohne Zoom-Analyse wird die Probe mit einem Verlustfaktor von 0,03 und weniger stark beeinflusst.
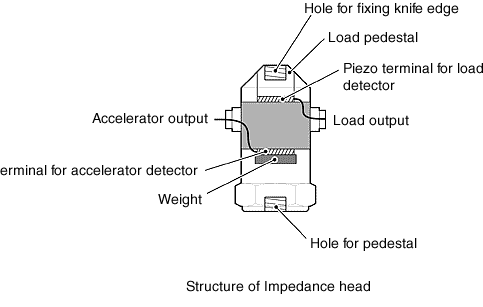
12.2 Impedanzkopf
Der Impedanzkopf hat die Struktur, bei der zwei Sensoren, der Kraftdetektor und der Beschleunigungsmesser in einem integriert sind. Er ist für das zentrale Anregungsverfahren als Detektor notwendig. Wenn der Anregungspunkt der Impedanz gemessen wird, wird der Impedanzkopf am Erreger befestigt, um die Probe zu vibrieren. Im Hinblick darauf, den Impedanzkopf in einem Thermostat anzuordnen, ist ein auf elektrische Ladung empfindlicher Impedanzkopf wünschenswert. Die Empfindlichkeit des Kraftdetektors und des Beschleunigungsmessers beträgt wünschenswerterweise 100 pC/N oder mehr und 1 pC/ms –2oder mehr, wenn man bedenkt, dass das Gewicht der Probe nur 100 g beträgt, die Anregungskraft nur 10 N. Wenn ein spannungsempfindlicher Impedanzkopf verwendet wird, ist es notwendig, die Temperaturobergrenze zu überwachen, und die Empfindlichkeit des Kraftdetektors und des Beschleunigungsmessers beträgt wünschenswerterweise 100 mV/N oder mehr und 1 mV/ms –2 oder mehr. Da der Abfallmodus auftreten kann, ist es vorzuziehen, dass die Höhe des Impedanzkopfes so niedrig wie möglich ist. Anschlussdrähte werden unter Berücksichtigung des Gleichgewichts zwischen vorne, hinten, links und rechts symmetrisch gezogen, und kurze Stecker sind wünschenswert.
12.3 Resonanz, Anti-Resonanz für die Central Exciting-Methode
Wenn die Impedanz (F-Kraft/V-Geschwindigkeit) mit der zentralen Anregungsmethode gemessen wird, erscheinen die Resonanzfrequenz und die Antiresonanzfrequenz abwechselnd, wie in der Abbildung unten gezeigt. Bei der Resonanzfrequenz ist die Anregungsleistung sehr klein und die Probe wird stark vibriert, während bei der Antiresonanzfrequenz die Anregungsleistung groß ist und die Probe nicht stark vibriert.
Beispielsweise ist die Mittenlage der zweiten Antiresonanz bei zentraler Anregung aufgrund der anderen Randbedingungen völlig anders als die zweite Resonanzmode der Zweipunktaufhängung.

Die folgenden Diagramme zeigen die Ergebnisse der Verlustfaktormessung der Dämpfungsstahlplatte bei unterschiedlicher Probenlänge und Temperatur. Wie gezeigt, gibt es Unterschiede zwischen Resonanzfrequenz und Antiresonanzfrequenz.
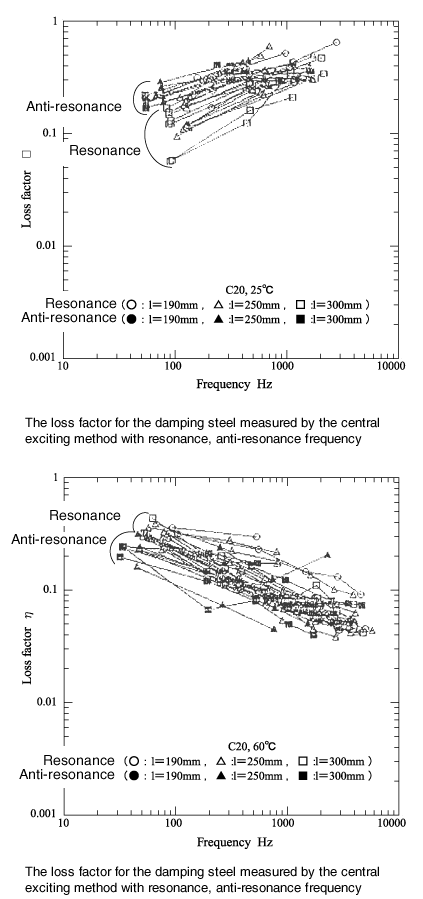
Wie in der Figur gezeigt, wird die nach rechts ansteigende Frequenzabhängigkeit stark auf der Antiresonanzseite gemessen, die nach rechts abfallende wird stark auf der Resonanzseite gemessen. Der oberste Strahl zeigt dieses Phänomen nicht.
12.4 Fehlerursachen
Probleme bei der Probenherstellung · Ungleichmäßige physikalische Eigenschaften, Maßfehler, schlechter Klebstoff · Arten von Klebematerialien · Dicke der Klebematerialien, temperaturbeständige Materialien
Temperaturkontrolle · Gleichmäßigkeit der Temperaturverteilung innerhalb der Probe · Der Energieverlust am Stützpunkt muss minimiert werden
13. Methodenauswahl (Cantilever-Methode und Central-Springing-Methode)
Bitte beachten Sie, dass die Cantilever-Methode und die zentrale Anregungsmethode die folgenden Eigenschaften in der Anwendung haben:
| Cantilever-Methode | Zentrale spannende Methode | |
| Einfaches Testen der Temperatur | ○ | △ |
| Korrespondenz mit der hohen Temperatur | × | Mit Vibrokammer |
| Klemmproblem | Ja | Nein |
| Messung des 1. Modus | Nicht verfügbar | Erhältlich |
| Messung des High-Times-Modus | schwer | Leicht |
| Massenabsage | Nicht benötigt | Erforderlich |
| Messung für einzelnes weiches Material | Erhältlich | Nicht verfügbar |
| Messung auf der Antiresonanzseite | schwer | Leicht |
| Preis | ○ | × |
14. Vergleiche von Verlustfaktoren, die mit verschiedenen Methoden erhalten wurden
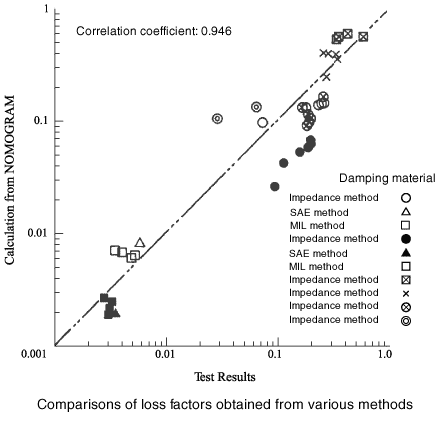
Aus den aus dem Cantilever-Verfahren gewonnenen Probendaten werden Verlustfaktor und E-Modul des Dämpfungsmaterials in Form eines reduzierten Frequenznomogramms berechnet. Dann wird unter Verwendung dieses Nomogramms der Verlustfaktor für die Impedanz-, SAE- und MIL-Methode wie folgt geschätzt. Die Beziehung zwischen dem geschätzten Verlustfaktor auf der vertikalen Achse und dem tatsächlichen Wert des Verlustfaktors, der durch Impedanz, SAE, MIL-Methode auf der horizontalen Achse berechnet wird, ist in der folgenden Abbildung dargestellt. Im Ergebnis dieser Abbildung beträgt der Korrelationskoeffizient 0,946, und der aus der Cantilever-Methode erhaltene Verlustfaktor stimmt gut mit dem aus der Impedanz-, SAE-, MIL-Methode erhaltenen überein.
15. Massenabsage
Wenn das zentrale Erregungsverfahren durchgeführt wird, wird der Verlustfaktor im Allgemeinen durch Messen der Antriebspunktimpedanz, Mobilität mit einem Impedanzkopf gemessen. In diesem Fall hat der Impedanzkopf selbst eine Masse zum Messen der Beschleunigung, selbst wenn die Kraft auf Null gesetzt wird, wird diese Masse tatsächlich durch den Kraftsensor gemessen. Daher werden das Gewicht der Probe selbst und die Masse gemessen, die Impedanz wird nicht richtig gemessen. Daher ist es notwendig, diese zusätzliche Masse im Voraus zu korrigieren. Dieser Vorgang wird als Massenlöschung bezeichnet.
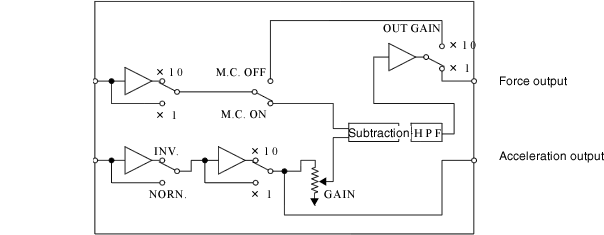
Die obige Abbildung zeigt ein Beispiel einer Massenlöschung, die folgende Abbildung zeigt ein Beispiel eines Testsystems zur Durchführung einer Massenlöschung.
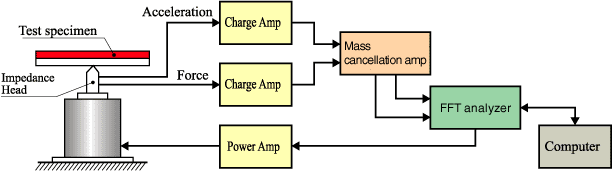
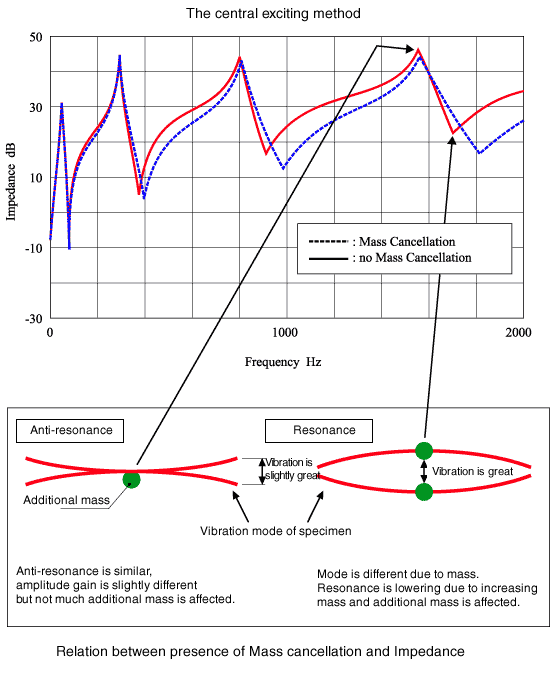
Die folgende Abbildung zeigt ein Beispiel für die Impedanz, die durch das obige System berechnet wird. Es stellte fest, dass die Resonanzfrequenz unterschiedlich war, indem eine Massenauslöschung oder keine Massenauslöschung durchgeführt wurde.
Berechnung durch Massenauslöschung, die durch FFT berechnet wird
Grün: Mobilität ohne Massenstornierung
Blau: Mobilität nach Massenauslöschung, erhalten aus Berechnung 1[(V / F)-(V / F 0 )]
Rot: Mobilität nach Massenauslöschung mit Massenauslöschungsverstärker
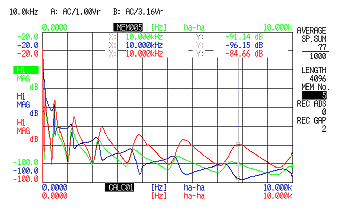
Grün: Mobilität ohne Massenlöschung
Blau: Mobilität nach Massenlöschung erhalten aus Berechnung 2 [(V / F)(1 / H)-(V / F 0 )(1 / H)](1 / H)
Rot: Mobilität nach Massenauslöschung mit Massenauslöschungsverstärker
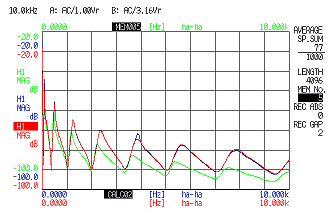
Falls die Wellenform der mechanischen Impedanz weggelassen wird, aber die Massenauslöschung durch FFT durchgeführt wird, kann die Funktion des Zählers F (mechanische Impedanz) wie folgt subtrahiert werden (F/V)-(F0 / V). Wenn der Nenner eine Funktion von F (Mobilität usw.) verwendet, bringen Sie zuerst F zum Zähler durch inverse Berechnung der Frequenzgangfunktion (1 / H), subtrahieren Sie die zusätzliche Masse durch die inverse Berechnung. Es ist notwendig, die inverse Berechnung durchzuführen und die Funktion zurückzugeben, die den ursprünglichen Nenner als F hat. Gemäß der Frequenzgangfunktion ohne Arbeit als FRF1, der Frequenzgangfunktion, die Arbeit hinzufügt, ohne Massenauslöschung als FRF2, der Frequenzfunktion nach Massenauslöschung als FRF3, die eigentliche Berechnung wie folgt:
FRF3 = 1/((1/FRF2)-(1/FRF1))
Die folgende Abbildung zeigt den Zusammenhang zwischen dem Vorhandensein von Massenauslöschung und dem Verlustfaktor als zentrale Anregungsmethode. Wenn der Verlustfaktor kleiner als 0,01 ist, ist ersichtlich, dass der Verlustfaktor je nach Vorhandensein einer Massenauslöschung leicht unterschiedlich ist.
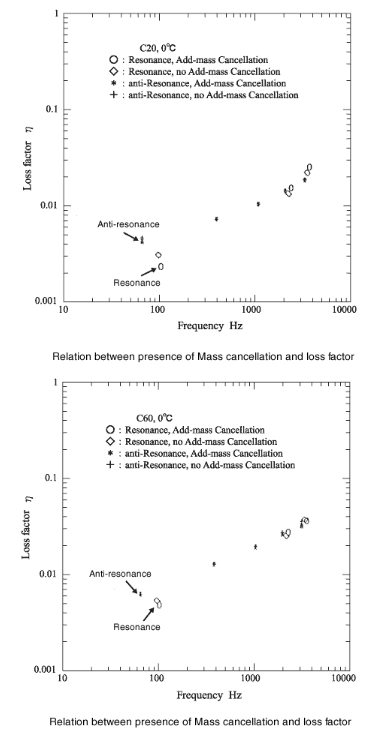
16. Notwendigkeit der FFT-Zoomanalyse
Das folgende Diagramm stellt dar, dass fünf Arten von Materialien mit unterschiedlichen Verlustfaktoren mit unterschiedlichen Frequenzauflösungen gemessen wurden, als eine FFT-Zoomanalyse durchgeführt wurde. Die horizontale Achse zeigt die Anzahl der FFT-Messpunkte innerhalb von -3 dB wie beim Halbwertsverfahren. Wenn die Zoom-Vergrößerung wie unten gezeigt erhöht wird, konvergiert das gemessene η allmählich auf den konstanten Wert. Wenn dieser Wert als wahr verwendet wird, werden die Fehler wie in der umgeschriebenen Grafik gezeigt berechnet.
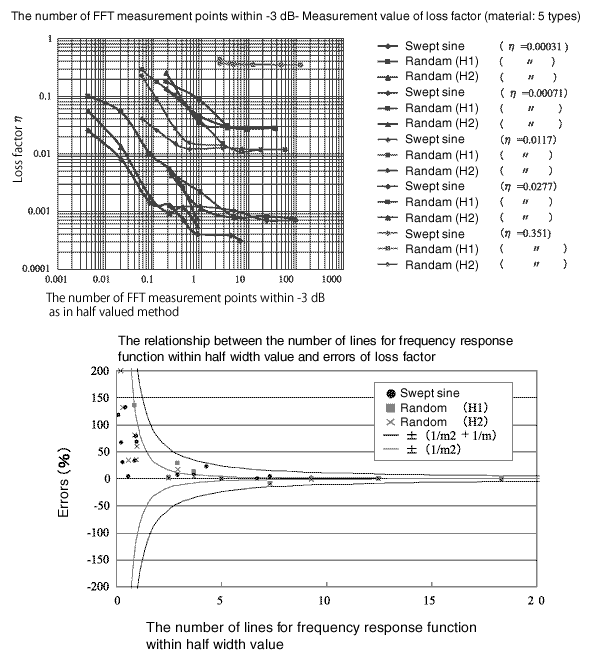
Wenn der Auflösungspunkt der FFT innerhalb der Halbwertsbreite etwa 15 Punkte beträgt, beträgt die Messgenauigkeit des Verlustfaktors etwa 1 %. Falls der Verlustfaktor klein ist, ist die Zoom-Analyse erforderlich.
17. Zoom-Analyse und Massenlöschung
Die folgende Abbildung zeigt die Messfehler des Verlustfaktors, die durch die Durchführung oder Nichtdurchführung von Zoomanalyse und Massenauslöschung verursacht werden. Indem sowohl die Zoomanalyse als auch die Massenlöschung durchgeführt werden, werden die Fehler am meisten minimiert. Bitte beachten Sie, dass der Unterschied des Verlustfaktors, der durch die Durchführung oder Nichtdurchführung der Zoomanalyse und der Massenlöschung verursacht wird, im Falle eines Verlustfaktors von 0,01 oder weniger bemerkenswert ist.
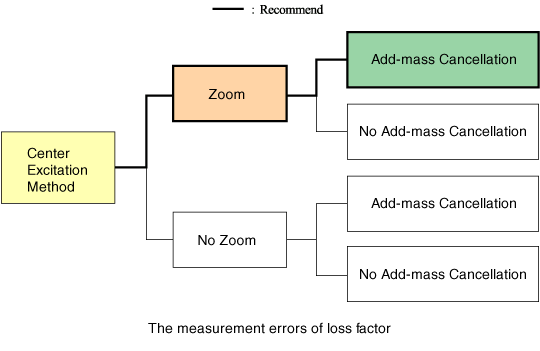
Das Durchführen einer Zoom-Analyse oder das Durchführen einer Massenauslöschung hat keinen großen Einfluss auf den Verlustfaktor.
18. Kurvenanpassung durch Verwendung von Pol-Null-Modellen für die Verlustfaktormessung
(Derzeit gilt es als die beste Kurvenanpassungsmethode zur Messung des Verlustfaktors, daher haben wir die Genehmigung von Prof. Hideo Suzuki vom Chiba Institute of Technology erhalten, das Papier so zu veröffentlichen, wie es ist.)
18.1 Einleitung
Mit den jüngsten Fortschritten in der Herstellungstechnik von Dämpfungsmaterialien machen wir praktischen Gebrauch von Materialien mit großen Verlustfaktoren. Für das genormte Messverfahren des Verlustfaktors inklusive ISO gibt es nur eine traditionelle Halbwertsmethode. Hier ist das Halbbreitenverfahren ein Verfahren, das durch η = (f 2 – f 1 )/f 0 definiert ist, das durch die Resonanzfrequenz f 0 berechnet wird, die aus den Schwingungsantwortcharakteristiken, wie etwa Amplitude, Geschwindigkeit, Beschleunigung und den Frequenzen, erhalten wird f1 und f2 _bei dem die Reaktion um 3 dB vom Resonanzspitzenpegel abfällt. Da jedoch in letzter Zeit Materialien mit einem Pegelunterschied zwischen Resonanz und Antiresonanz von weniger als 3 dB entwickelt wurden, ist die Halbwertsmethode für solche Materialien überhaupt nicht brauchbar. Darüber hinaus wird als neuerer technischer Trend ein Versuch unternommen, einen Verlustfaktor aus der Schärfe der Resonanzfrequenzcharakteristiken und der Schärfe der Antiresonanzcharakteristiken zu erhalten. Anstatt beispielsweise die Spitze (die Resonanzeigenschaften) der Frequenzgangfunktionen zu verwenden, die aus [Geschwindigkeit/Kraft] erhalten werden, wird der Verlustfaktor aus der unteren (den Antiresonanzeigenschaften) erhalten. Obwohl die Beziehung zwischen der Schärfe der Antiresonanz und dem Wert des Verlustfaktors bei dieser Frequenz nicht klar ist. Aus dem oben genannten Grund wird empfohlen, Pol-Null-Modelle zu verwenden, bei denen der Verlustfaktor durch Kurvenanpassung an die Eigenschaften von [Geschwindigkeit/Kraft] oder [Kraft/Geschwindigkeit] gemessen wird. Dieses Papier wird die Übersicht erläutern.
18.2 Die Pole-Null-Modelle
Das Pol-Null-Modell ist eine Charakteristik, die die Antwortcharakteristik am Anregungspunkt wie folgt ausdrückt:
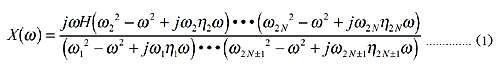
oder
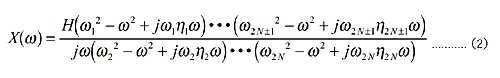
η n stellt die Dumpfheit der Eigenschaften bei jeder Resonanz und Antiresonanz dar (im Falle einer Resonanz ist es ein Verlustfaktor). Ω n steht für Resonanz oder Antiresonanz, H steht für Konstante. (1) und (2) stellen Ätherimpedanz ([Kraft/Geschwindigkeit]) oder Mobilität ([Geschwindigkeit/Kraft]) dar, hier ist Mobilität. Die Beweglichkeit des Auslegers entspricht (2), die Beweglichkeit des Frei-Frei-Strahls entspricht (1), da jede Beweglichkeit zunimmt oder abnimmt, je nachdem sich die Frequenz Null nähert. Beim Anpassen an die Impedanzcharakteristik kann das Inverse genommen werden und daher können die Gleichungen ersetzt und angewendet werden. Die größte Eigenschaft des Pol-Null-Modells besteht darin, dass der Verlustfaktor (im Fall von Antiresonanz der Einfachheit halber auch als Verlustfaktor bezeichnet) explizit angezeigt wird, was bedeutet, dass die Schärfe der Peak- und Bottom-Eigenschaften unabhängig voneinander definiert ist. Zu Ihrer Information wird die für die Modusanalyse verwendete Berechnung wie folgt gezeigt. Der Verlustfaktor bei Resonanz kann nur explizit eingegeben werden.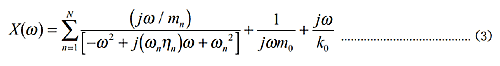
18.3 Fehlerfunktion für die Kurvenanpassung
Eine Fehlerfunktion, die die Unterschiede zwischen tatsächlichen Daten und Modelleigenschaften ausdrückt, muss entwickelt werden, um den gleichen Fehler an die Spitze und den Boden der Eigenschaften anzupassen. Es wird häufig für die Fehlerfunktion wie folgt verwendet:
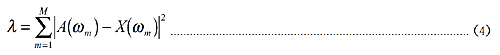
A(Ω m) sind tatsächliche Eigenschaften, X(Ω m) sind Modelleigenschaften. Da die Zahl bei Resonanz groß ist, trägt sogar der gleiche Fehlerprozentsatz stark bei, und der charakteristische Fehler bei Antiresonanz wird vernachlässigt. Es wurden 2 Fehlerfunktionen eingeführt, um dieses Problem zu lösen.
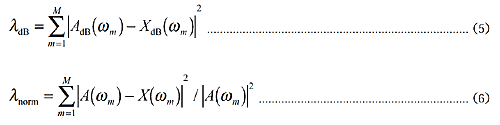
Formel (5) ist ein Verfahren, das eine Charakteristik verwendet, die die Frequenzgangfunktionalität in Dezibel zum Anpassen ausdrückt. Formel (6) ist ein Verfahren, bei dem die gleiche Fehlerrate in der Spitze und im Boden zu λ mit der gleichen Größe beiträgt, indem sie mit den gemessenen Eigenschaften normalisiert wird. Durch die Verwendung dieser Fehlerfunktionen können die Resonanz- und Antiresonanzeigenschaften gleichzeitig angepasst werden.
18.4 Antrag auf Modelldaten
Es ist verfügbar, die Eigenschaften aus Formel (1) oder (2) zu berechnen, sie als tatsächliche Messdaten zu betrachten, eine Anpassung durchzuführen, zu prüfen, wie nahe an dem wahren Wert erhalten werden kann, und die Korrektheit des Algorithmus zu verifizieren. Abb. 1 zeigt das Ergebnis. Die dünne durchgezogene Linie mit vier Polen und Nullstellen hat die anzupassende Charakteristik und wird berechnet, indem der Verlustfaktor angegeben wird, der den Resonanz- und Antiresonanzfrequenzen des Typ-B-Pol-Null-Modells in Abb. 1 entspricht. Die Resonanz- und Anti- Resonanzfrequenzen entsprechen der Frequenzverteilung bei der zentralen Anregung mit Rechteckstrahl. Die Verlustfaktoren 0,1, 0,2 und 0,3 werden jeder Resonanz und Antiresonanz passend zugeordnet. Die dicke Linie errechnet sich aus dem Verlustfaktor, der einheitlich auf einen Anfangswert von 0,15 gegeben ist. Es wird berechnet, indem die Dezibel-Fehlerfunktion angegeben wird. Nach der Anpassung mit der Dezibel-Typfehlerfunktion wird der richtige Parameterwert mit einer Genauigkeit von 8 Stellen oder mehr erhalten. (Die konvergierte Kurve überlappt die dünne Linie.) Der Vorteil des Erhaltens des Verlustfaktors durch Kurvenanpassung besteht darin, dass die Frequenzauflösung beim Messen viel grober sein kann als die Halbwertsmethode. Die Anpassung ist verfügbar, auch wenn sie grob genug ist, um bei niedrigen Frequenzen wie ein Liniendiagramm auszusehen, wie in Abb. 1 gezeigt.
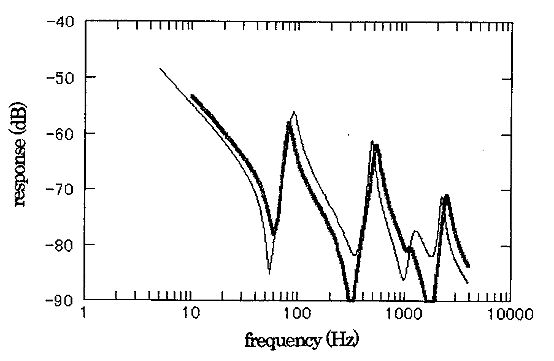
18.5 Tatsächliche Messung mit der Kurvenanpassungsmethode
Entsprechung zum kleinen Verlustfaktor
Die Messfehler für den Verlustfaktor überlagern das Diagramm, das die Anzahl der Messpunkte innerhalb der halben Wertbreite wie in der folgenden Abbildung darstellt. Es ist ersichtlich, dass bei einem Messpunkt von etwa 0,3 Punkt innerhalb der Halbwertsbreite die Fehler innerhalb weniger Prozent liegen.
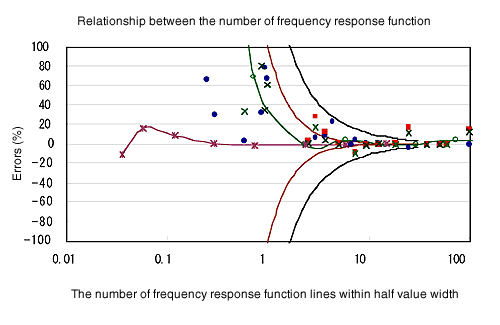
schwarze Linie: Halbwertsbreitenmethode ±(1/m2+1/m)Linie
rote Linie: Halbwertsbreitenmethode ±(1/m2)Linie
violette Linie: Kurvenanpassungsmethode notwendige Linie
Korrespondenz zum großen Verlustfaktor
Die Frequenzgangfunktionalität, die nicht mit der Halbwertsbreitenmethode unter Simulation η= 0,7, 1,0, 1,2 gemessen werden kann, wird durch Kurvenanpassung mit der dB-Methode wie unten gezeigt durchgeführt. Es ermöglicht eine Messung mit hoher Genauigkeit bis zur 6. Resonanzfrequenz bei etwa 0,7 Verlustfaktor, bis zur 3. Resonanzfrequenz bei etwa 1,0, 1,2 Verlustfaktor.
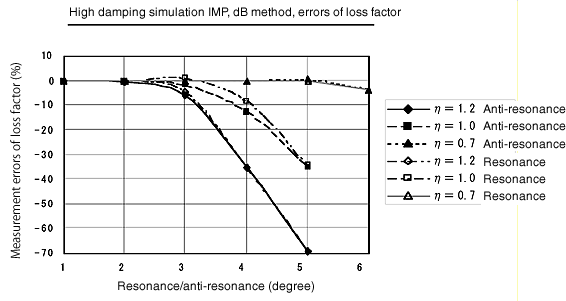
19. Hängende Methode mit zwei Punkten
Dies ist eine Methode zum Aufhängen eines Knotens für jeden Vibrationsmodus. Da es vom kleinsten Verlustfaktor gemessen werden kann, indem es an einer Position aufgehängt wird, an der es sich nicht bewegt, wird es hauptsächlich zur Messung des Verlustfaktors für Einzelmetallprodukte verwendet. Der Nachteil dieser Methode ist, dass die Hängeposition für jeden Modus geändert werden muss. Es ist üblich, eine nicht berührbare elektromagnetische Erregung für die Erregung zu verwenden und sie als elektromagnetischen Geschwindigkeitssensor für die Reaktion zu verwenden. (Bezüglich elektromagnetischer Anregung/Detektor siehe Geräte für Cantilever-Methode.
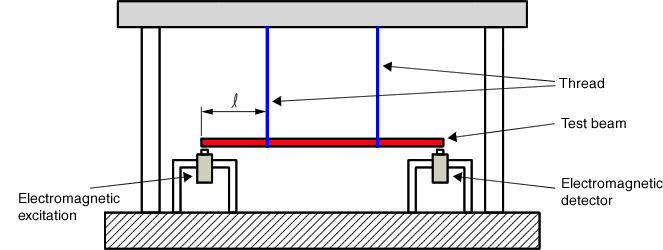
Position von 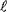
| Grad | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Position des Knotens | 22.42 | 13.21 | 9.44 | 7.35 | 6.01 |
| 50.00 | 35.58 | 27.68 | 22.65 | ||
| 86,79 | 64.42 | 50.00 | 40.91 | ||
| 90.56 | 72.32 | 59.09 | |||
| 92,65 | 77.35 | ||||
| 93,99 |
*Die Position vom linken und rechten Ende wird in % ausgedrückt, wenn die Länge des Prüfbalkens 100 % beträgt. Wenn es viele Knoten gibt, können Sie überall hängen.
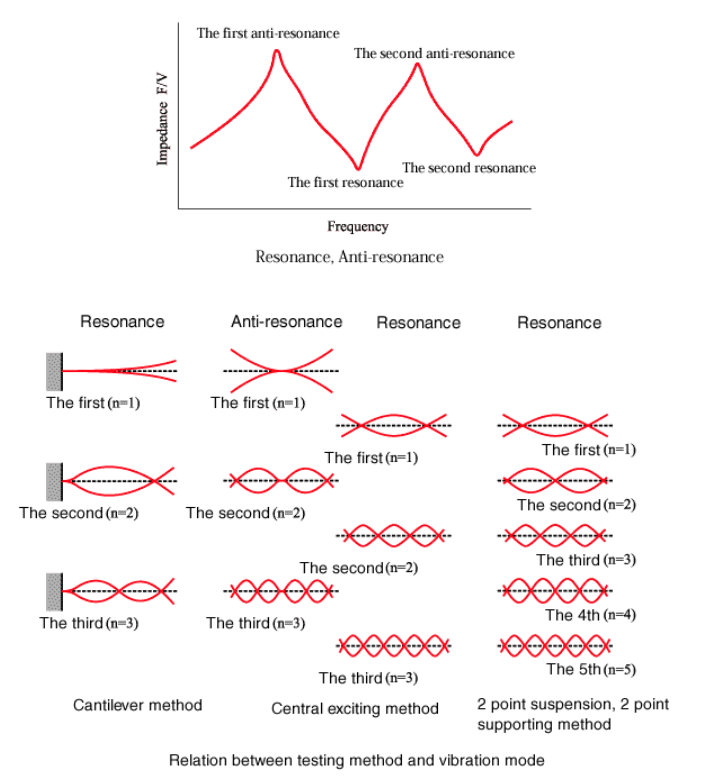
20. Der Verlustfaktor hängt vom Vibrationsmodus ab
Gemäß der Beziehung zwischen dem Testverfahren und dem Vibrationsmodus wie unten, ist der Vibrationsmodus durch das Cantilever-Verfahren und das zentrale Erregungsverfahren gleich, wenn die Länge des Probenbalkens für das Cantilever-Verfahren die Hälfte der Länge des Probenbalkens für die Mitte beträgt spannende Methode. Der Vibrationsmodus durch das Aufhängen an zwei Punkten, das Stützverfahren an zwei Punkten bei Resonanz und das zentrale Anregungsverfahren bei Resonanz ist gleich.
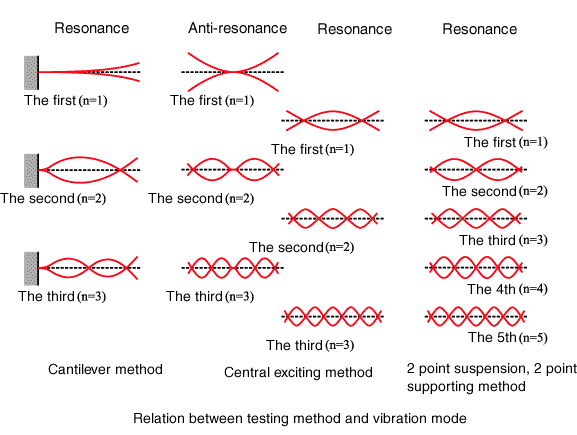
Die folgenden 4 Abbildungen zeigen den Vergleich des Verlustfaktors für 1. die Cantilever-Methode bei Resonanz und die zentrale Anregungsmethode bei Antiresonanz, und 2. die Methode mit zwei Punkten hängend, zwei Punkte stützend bei Resonanz und die Methode mit zentraler Anregung bei Antiresonanz. Resonanz. Diese Zahlen finden es wie folgt:
Die Cantilever-Methode ≠ die zentrale Anregungsmethode (bei Antiresonanz)
Die zwei Punkte hängende, zwei Punkte tragende Methode≠ die zentrale Anregungsmethode (Resonanz)
Die gültige Länge des Probeträgers
2 x Cantilever-Methode = die zentrale Anregungsmethode
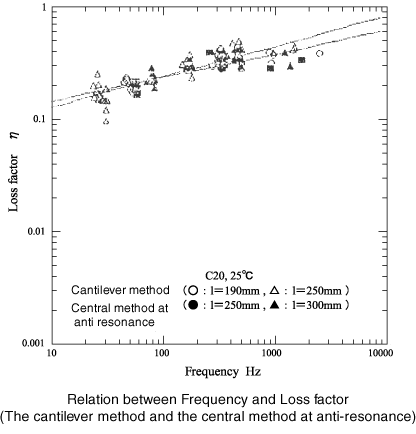
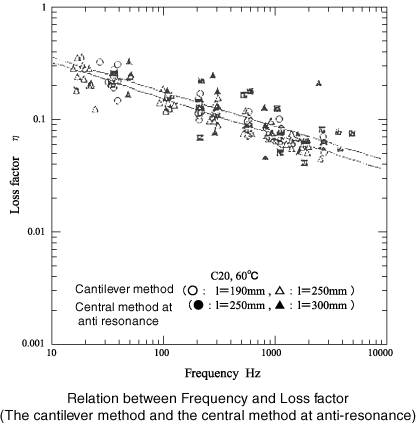
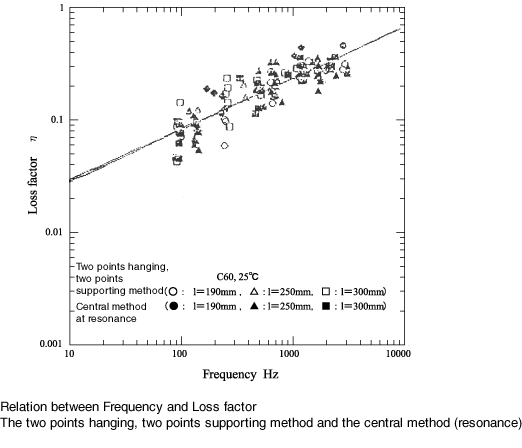
21.Um eine genaue Frequenzgangfunktion zu erhalten
Hinweise zur Verwendung des FFT-Analysators
Zunächst können Sie überprüfen, ob bei Verwendung der Dämpfung eine Amplitudenabhängigkeit vorliegt oder nicht. Wenn es eine Amplitudenabhängigkeit gibt, müssen Sie mit dem Dämpfungsfaktor messen, da die Frequenzgangfunktion nicht symmetrisch ist. Der synchronisierte Sin-Sweep ist für das Eingangssignal des Exciters am besten geeignet. Es ist wünschenswert, dass der FFT-Analysator über eine automatische Bereichsfunktion verfügt, die automatisch seinen Spannungsbereich, den Ein-/Ausgangsspannungsbereich anpasst und die Verstärkung der Frequenzgangfunktion widerspiegelt. Es ist besser, eine Funktion zu haben, die den Pegel des Ausgangssignals entsprechend der Verstärkung der Frequenzgangfunktion ändert. Das Signal mit den folgenden Eigenschaften wird empfohlen, wenn die Messung des Sin-Sweeps einige Zeit in Anspruch nimmt.
21.1 Sweep-Sinussignal
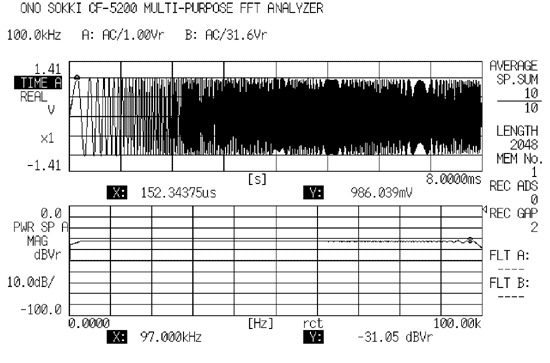
Eigenschaften
Es ist ein gewobbeltes Signal mit hoher Sinuswelle. Der Crest-Faktor (Maximal-/Effektivwert) ist mit 1,4 sehr gering. Dabei ist der Konzentrationsgrad des Signals sehr hoch. Die Leckagefehler treten nicht auf, da eine Synchronisation mit der FFT-Rahmenanalyse erreicht wird und das rechteckige Fenster als Fensterfunktion verwendet werden kann. Es gibt keinen Additionseffekt aufgrund des immer gleichen Signals, jedoch wird es in letzter Zeit häufig verwendet, da die genaue Frequenzgangfunktion in kurzer Zeit gemessen werden kann. Es handelt sich offenbar um ein schmalbandig gewobbeltes Signal auf dem Gerät, bei dem die Signalsynchronisation, die Frequenzbandbegrenzung, die Auflösungsänderung durch Frequenzzoomen erfolgen kann. Die folgende Abbildung gilt für das bandbegrenzte gewobbelte Signal.
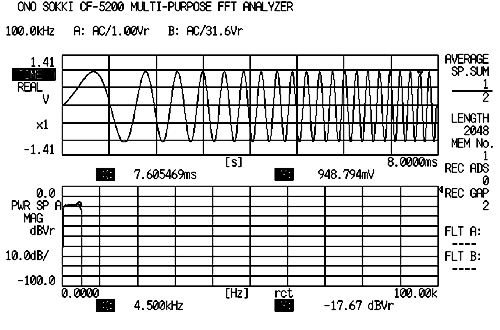
21.2 Mehrere Sinussignale
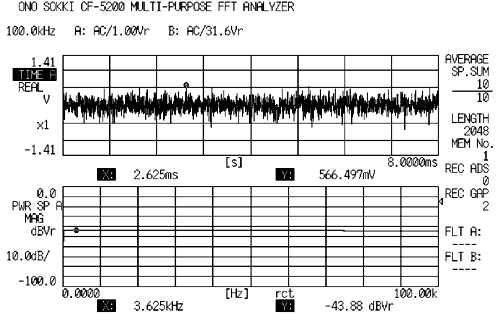
Eigenschaften
Sie bestehen aus Multi-Sinuswellen, die an allen Auflösungspunkten Sinuswellen auf gleichem Niveau haben. Der Crest-Faktor liegt bei etwa 3. Der Konzentrationsgrad des Signals ist moderat. Die Leckagefehler treten nicht auf, da eine Synchronisation mit der FFT-Rahmenanalyse erreicht wird und das rechteckige Fenster als Fensterfunktion verwendet werden kann. Es gibt keinen Additionseffekt aufgrund des immer gleichen Signals, jedoch wird es in letzter Zeit häufig verwendet, da die genaue Frequenzgangfunktion in kurzer Zeit gemessen werden kann. Wenn die logarithmische Auflösung durch Anordnen von Sinuswellen in logarithmischen Intervallen erhalten wird, kann die logarithmische Auflösung gemessen werden, indem die logarithmische Auflösungsfrequenz auf der FFT-Seite ausgewählt und angezeigt wird.
Die folgende Abbildung gilt für die bandbegrenzten Mehrfachsinussignale.
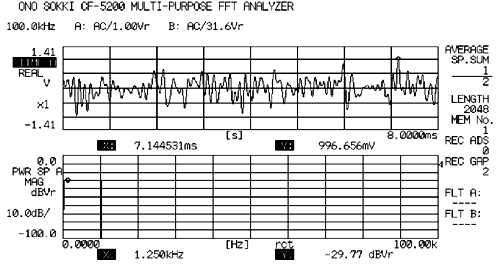
21.3 Impulssynthese
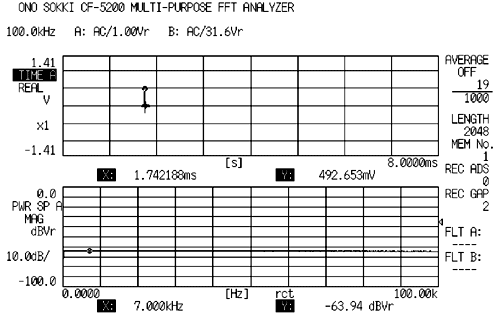
Eigenschaften
Es ist das Signal, das die 1. Welle der Sinuswelle synthetisiert, um sich an die Spitzenposition anzupassen. Der Crestfaktor liegt bei etwa 30. Es ist einfach, der Zoomanalyse im Vergleich mit dem normalen Impuls zu entsprechen. Richtig, der Anfang und das Ende ist „Null“. Die Leckagefehler treten nicht auf, da eine Synchronisation mit der FFT-Rahmenanalyse erreicht wird und das rechteckige Fenster als Fensterfunktion verwendet werden kann. Er kann für das Eingangssignal für den Exciter im Dämpfungsratenverfahren verwendet werden.
21.4 Zufallssignal
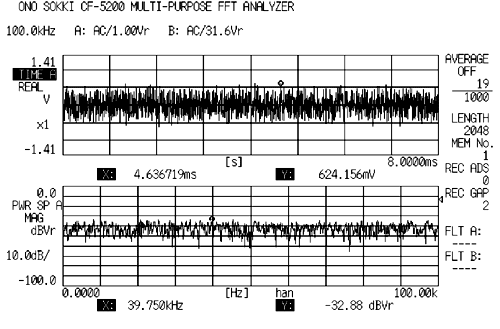
Eigenschaften
Normalerweise wird das Signal der M-Serie verwendet und der Scheitelfaktor liegt bei etwa 3. Der Konzentrationsgrad des Signals ist gering. Da es alle Frequenzsignale hat, kann es für die Zoomanalyse verwendet werden. Das Hanning-Fenster wird normalerweise verwendet, da es keine Synchronisation mit der FFT-Rahmenanalyse erhält. Wenn jedoch der Verlustfaktor gemessen wird, ist das rechteckige Fenster vorzuziehen. Bei der Verwendung des Hanning-Fensters wird auf die Leckfehler, aber auch auf die Messuntergrenze des Verlustfaktors geachtet. Da dies auch eine Bandbegrenzung aufweist, ist es wünschenswert, die Bandbegrenzung innerhalb der Zoombandbreite zu regeln, wenn eine Zoomanalyse durchgeführt wird. Das Hinzufügen ist sehr effektiv, daher ist es notwendig, genug hinzuzufügen, da von Zeit zu Zeit viele Frequenzen fehlen. Für die Messung des Geräts mit nichtlinearen Elementen wird der Burst Random verwendet
22. Window-Funktion zur Messung des Verlustfaktors
Die Frequenzgangfunktion wird transformiert, wenn der Verlustfaktor durch die Fensterfunktion gemessen wird. Die folgenden Abbildungen zeigen die untere Grenze für die Messung des Verlustfaktors bei Messung durch die einzelnen Fensterfunktionen.
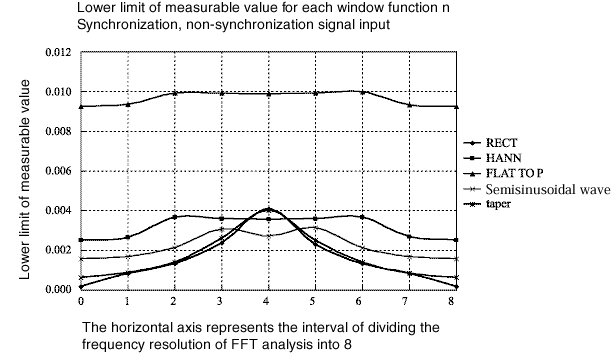
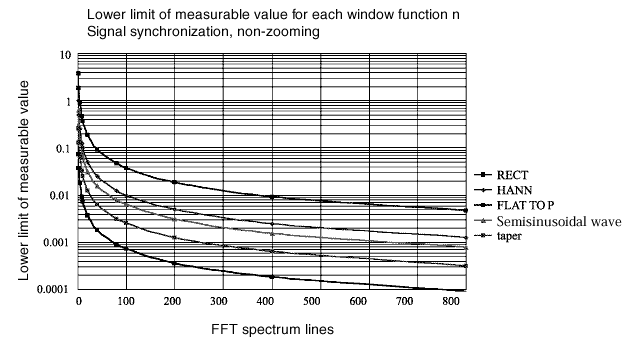
Die obigen Zahlen finden es wie folgt:
Die Flat-Top-Window-Funktion ist für die Messung des Verlustfaktors nicht geeignet. Die quadratische Fensterfunktion ist die beste, außer dass das Signal in die Worst-Case-Auflösung und die Mittenposition der Auflösung eingegeben wird.
Es ist üblich, dass die Hanning-Fensterfunktion als Fensterfunktion verwendet wird, wenn das Signal asynchron ist. Die quadratische Fensterfunktion ermöglicht es jedoch, den niedrigsten Verlustfaktor nur dann genau zu messen, wenn der Verlustfaktor gemessen wird (falls ein η größer als –13 dB von der Spitze erhalten wird).
Die Verjüngungsfensterfunktion wird verwendet, wenn die Kohärenz durch das rechteckige Fenster verringert wird.
Je näher der Resonanzpunkt an der linken Seite des FFT-Schirms liegt, desto größer ist der Einfluss der Fensterfunktion. Beispielsweise ist die untere Messgrenze für die 10. Zeile der FFT η = 0,15 ohne Zoomen, aber unter Verwendung des Hanning-Fensters. Die Tatsache, dass sich die Spitze der Wellenform für die Frequenzgangfunktion auf der linken Seite des Bildschirms befindet, bedeutet, dass die Niederfrequenzresonanz / Antiresonanz durch Hochfrequenz gemessen wird. Das Verschieben der Spitze nach rechts bedeutet (1) Absenken des Frequenzbereichs, (2) Ausführen von Zoom-Frequenzen, daher ist es notwendig, eine Zoom-Analyse durchzuführen. Ein weiterer Vorteil der Zoom-Analyse ist, dass die hervorstehende Transformation der Impulsantwort reduziert wird, wenn der Zeitrahmen länger ist. Darüber hinaus kann mit zunehmender Frequenzauflösung eine Verringerung des Fehlers erwartet werden. Ein ähnlicher Effekt kann erwartet werden, indem die Anzahl der FFT-Punkte erhöht wird. Es gibt das Gerät, das kürzlich das Spektrum von 25.600 Linien mit 65.536 FFT-Punkten berechnet. Wenn der Verlustfaktor bis zu einem gewissen Grad groß ist, ist es einfach, ihn ohne Zoomanalyse zu verwenden.
23. Berechnung des Elastizitätsmoduls
Die Berechnung des Elastizitätsmoduls, erhalten aus einer Messung von reinem Material, und die Berechnung, welcher Verlustfaktor, Elastizitätsmodul für einzelnes Dämpfungsmaterial, erhalten wird aus Verlustfaktor, Elastizitätsmodul, gemessen durch den Verbindungstyp (doppelt, drei Schichten) mit RKU (Ross, Kerwin , Unger) Gleichung sind wie folgt dargestellt:
23.1 Reines Material
Resonanzfrequenz f n (Hz), Halbwertsbreite δ f n (Hz), Länge des Probebalkens ![]() (m), Dicke des Probebalkens h (m), mittlere Dichte des Probebalkens ρ (kg/m 3 ):
(m), Dicke des Probebalkens h (m), mittlere Dichte des Probebalkens ρ (kg/m 3 ):
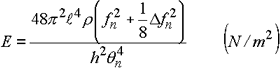
Wenn der Dämpfungswert klein ist, wird 1/8 δ f n 2 ignoriert
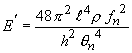
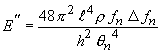
und Verlustfaktor η ist
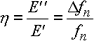
Bei Verwendung des Cantilevers und der zentralen Anregungsmethode mit Antiresonanz:
|
Grad n | n _ | θ n 4 |
|---|---|---|
| 1 | 1,87510 | 12.36 |
| 2 | 4.69409 | 485.5 |
| 3 | 7,85476 | 3806.6 |
| 4 | 10.99554 | 14617.3 |
| 5 | 14.13717 | 39943.8 |
| 6 | 17.27876 | 89135.4 |
| 7 | 20.42035 | 173881.2 |
| 8 | 23.56194 | 308208.2 |
Wie folgt + π
Geben Sie im Fall der Auslegermethode die volle Länge außer dem Greifrand wie in Gleichung (1) ein.
Geben Sie im Falle des zentralen Anregungsverfahrens mit Antiresonanz die halbe Länge von in Gleichung (1) ein.
Wenn Sie das zentrale Anregungsverfahren mit Resonanz verwenden, erhalten Sie die Resonanzfrequenz und verwenden Sie den folgenden Wert für θ n.
| Grad n | n _ | θ n 4 |
|---|---|---|
| 1 | 4.73004 | 500.56 |
| 2 | 10.99561 | 14617.6 |
| 3 | 17.27876 | 89135.4 |
| 4 | 23.56194 | 308208.2 |
| 5 | 29.84513 | 793403.1 |
| 6 | 36.12831 | 1703690.0 |
| 7 | 42.41150 | 3235448.8 |
| 8 | 48.69468 | 5622456.0 |
Wie folgt + π
wird in voller Länge eingegeben
Aufhängemethode an zwei Punkten mit freien Enden
| Grad n | n _ | θ n 4 |
|---|---|---|
| 1 | 4.73004 | 500.56 |
| 2 | 7,85320 | 3803.5 |
| 3 | 10.99561 | 14617.6 |
| 4 | 14.13717 | 33943.8 |
| 5 | 17.27876 | 89135.4 |
| 6 | 20.42035 | 173881.2 |
| 7 | 23.56194 | 308208.2 |
Wie folgt + π
wird in voller Länge eingegeben
Bei höherem Grad ist die Differenz zwischen θ n+1 und θ n fast gleich π
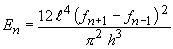
Die obige Berechnung, welcher Gradfaktor θ n und die Dichte ρ eliminiert werden, ist nützlich, wenn Sie sich über den Grad nicht sicher sind.
23.2 Die laminierten Verbundplatten

Der Verlustfaktor und der E-Modul eines einzelnen Dämpfungsmaterials können durch die folgende Berechnung aus den Daten des Grundmaterials selbst und der Verbundprobe berechnet werden, wenn der E-Modul-Anteil E 2 / E 1 = M, der Dickenanteil d 2 / d 1 eingegeben wird = T, Dichterate ρ 2 / ρ 1 = d.
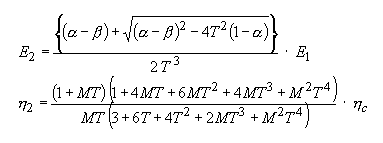

Der Verlustfaktor und der Elastizitätsmodul eines einzelnen Dämpfungsmaterials können durch die folgende Berechnung berechnet werden, wenn die Dickenrate d 2 / d 1 = T, die Dichterate ρ 2 / ρ 1 = d eingegeben wird.
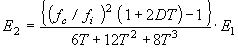
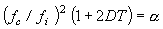
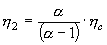
Dies gilt nur, wenn
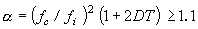
23.4 Schubmodul und Verlustfaktor für die Verbundplatten mit dem Dämpfungsmaterial zwischen Tragschicht und Zwangsschicht

Der Verlustfaktor und der Elastizitätsmodul eines einzelnen Dämpfungsmaterials können durch die folgende Berechnung berechnet werden, wenn die Dickenrate d 2 / d 1 = T, die Dichterate ρ 2 / ρ 1 = d eingegeben wird.
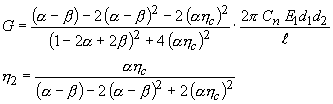
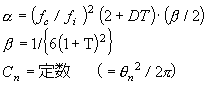
Dies gilt nur, wenn
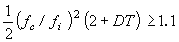
24. Physikalische Eigenschaft von viskoelastischen Materialien
Das Polymermaterial liegt in einem Zustand vor, in dem Kristallin und Nichtkristallin gemischt sind, während jede Molekülkette zufällig verwickelt ist, und die Temperatur-/Frequenzabhängigkeit von der molekularen Viskoelastizität abhängt. Die Molekülketten dieser Materialien haben verschiedene Bewegungsmodi, und jeder Modus setzt Energie bei einer bestimmten Temperatur und Frequenz frei. Die Dämpfungsleistung wird am größten im Übergangszustand, wo diese Molekularbewegung aktiv wird. Die lokale Bewegung der Hauptkette des Materialmoleküls im Glaszustand ändert sich in die Mikro-Brownsche Bewegung im Übergangszustand, was den größten Verlust ergibt. Die Temperatur-Frequenz-Überlagerung, WLF-Gleichung (Williams, Landel, Ferry) ist in diesem Übergangszustand abgeschlossen.
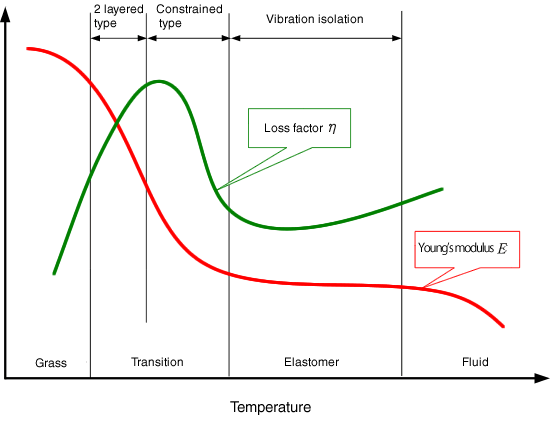
Die Temperatureigenschaften von viskoelastischen Materialien
24.1Temperatur-Frequenz-Überlagerung
Der komplexe Elastizitätsmodul (längs-, querelastisch) von viskoelastischen Materialien wie Polymer und Gummi, die als Dämpfungsmaterialien verwendet werden, drückt eine Funktionalität von Temperatur T und Frequenz f aus. Es ist bekannt, dass, wenn eine bestimmte Temperatur T 0 als Referenztemperatur festgelegt wird, indem der komplexe Elastizitätsmodul auf der vertikalen Achse und die Frequenz auf der horizontalen Achse bei der Temperatur T 1 genommen werden und dies in Richtung der horizontalen Achse übertragen wird, eine Übereinstimmung vorliegt der komplexe Elastizitätsmodul bei der Referenztemperatur T 0. Dies bedeutet, dass eine höhere Temperatur einer niedrigeren Frequenz entspricht (längere Zeit), eine niedrigere Temperatur einer höheren Frequenz entspricht (kürzere Zeit). Die Temperatur-Frequenz-Überlagerung ermöglicht es, auf diese Weise Temperaturänderungen in Frequenzänderungen umzuwandeln. Da die Dämpfungseigenschaften (dynamische Eigenschaften) des Dämpfungsmaterials sowohl von der Temperatur als auch von der Frequenz abhängen, ist eine dreidimensionale Anzeige erforderlich, um den Elastizitätsmodul und den Verlustfaktor für beide Parameter auszudrücken. Dann ist die Temperatur-Frequenz-Überlagerung wirksam. Die Temperatur-Frequenz-Überlagerung ist sehr nützlich für viskoelastische Materialien (insbesondere Glasübergangszustand). Durch Ersetzen der Temperaturänderung durch Frequenz (reduzierte Frequenz) können die dynamischen Eigenschaften des Dämpfungsmaterials in zwei Dimensionen ausgedrückt werden. Das bedeutet, die Temperatur-Frequenz-Überlagerung zu finden, die beide Kennwerte des Elastizitätsmoduls und des Verlustfaktors gleichzeitig erfüllt. Mit anderen Worten, das Gesetz, dass eine Änderung der Temperatur um T gleichbedeutend mit einer Änderung der Frequenz um f ist, wird so gefunden, dass es in einem weiten Temperaturbereich gleichzeitig sowohl auf den Elastizitätsmodul als auch auf den Verlustfaktor angewendet werden kann Frequenzbereich. Die Temperatur-Frequenz-Überlagerung wurde auf dem Gebiet der Rheologie von Polymermaterialien erforscht, und die bekannteste ist die WLF-Gleichung, die die Temperaturabhängigkeit des für viele Polymermaterialien erhaltenen Verschiebungsfaktors &agr;T zeigt. Das Gesetz, dass eine Änderung der Temperatur um T einer Änderung der Frequenz um f entspricht, wird so gefunden, dass es in einem weiten Temperatur- und Frequenzbereich gleichzeitig auf den Elastizitätsmodul und den Verlustfaktor angewendet werden kann. Die Temperatur-Frequenz-Überlagerung wurde auf dem Gebiet der Rheologie von Polymermaterialien erforscht, und die bekannteste ist die WLF-Gleichung, die die Temperaturabhängigkeit des für viele Polymermaterialien erhaltenen Verschiebungsfaktors &agr;T zeigt. Das Gesetz, dass eine Änderung der Temperatur um T einer Änderung der Frequenz um f entspricht, wird so gefunden, dass es in einem weiten Temperatur- und Frequenzbereich gleichzeitig auf den Elastizitätsmodul und den Verlustfaktor angewendet werden kann. Die Temperatur-Frequenz-Überlagerung wurde auf dem Gebiet der Rheologie von Polymermaterialien erforscht, und die bekannteste ist die WLF-Gleichung, die die Temperaturabhängigkeit des für viele Polymermaterialien erhaltenen Verschiebungsfaktors &agr;T zeigt.
24.2 WLF-Gleichung
Die Beziehung zwischen dem Verschiebungsfaktor α T und der Temperatur T wurde für verschiedene viskoelastische Materialien analysiert und als Williams-Landel-Ferry (WLF)-Gleichung wie folgt angeordnet:
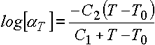
Gleichung 1
C1 und C2 sind Konstanten und werden so ausgewählt, dass sie mit der Beziehung zwischen dem Verschiebungsfaktor &agr;T und [T – T0] übereinstimmen.
Herleitung der WLF-Gleichung
Wenn ein amorphes Polymer (nicht kristallin) ein Relaxationsphänomen zeigt, wird angenommen, dass der Raum, in dem sich das Segment bewegen kann, das heißt das freie Volumen, die Mobilität und innere Viskosität des Segments dominiert. Aus der Viskositätsgleichung von doolittles basierend auf dem Konzept des freien Volumens
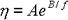
Gleichung 2
seinen natürlichen Logarithmus nehmen,
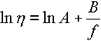
Gleichung 3
Das Obige stellt die Beziehung zwischen dem Elastizitätsmodul η und dem freien Volumen im Sinne der Molekulartheorie dar. f ist die freie Volumenrate, B ist fast 1. Dann lautet die Doolittle-Gleichung wie folgt:
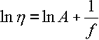
Gleichung 4
Hier ist ein Vergleich, die Viskosität η T bei beliebiger Temperatur T mit der Viskosität η T g am Glasübergangspunkt T g . Der Elastizitätsmodul dieser Temperaturen ist
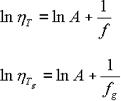
Gleichung 5
f 、f g ist die freie Volumenrate bei T と T g . Betrachtet man die Temperaturabhängigkeit der Relaxationszeit T ebenfalls als Doolittle-Typ, gilt folgende Gleichung:
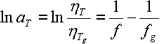
Gleichung 6
Die nächste Frage ist, wie man die Temperaturabhängigkeit des freien Volumenanteils f ausdrückt. Hinsichtlich des Verhältnisses zwischen spezifischem Volumen und Temperatur unterscheidet sich der Wärmeausdehnungskoeffizient im Glaszustand nicht wesentlich vom Kristallzustand, steigt aber bei Überschreitung von T g stark an. Wenn die Temperaturabhängigkeit von f fast die gleiche ist wie oben erwähnt,
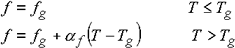
Gleichung 7
αf ist der Koeffizient der Differenz des freien Volumenanteils über Tg
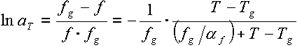
Gleichung 8
Umrechnung in den dekadischen Logarithmus,
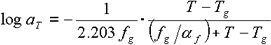
Gleichung 9
Die obige Gleichung hat dieselbe Formel wie die vorherige WLF-Gleichung (Gleichung 1). Durch Vergleich der Koeffiziententeile ist ersichtlich, dass die Koeffizienten C 1 und C 2 in der WLF-Gleichung wie folgt sind:
WLF-Gleichung
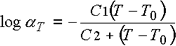
Gleichung 1
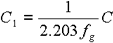
Gleichung 10
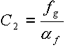
Gleichung 11
C 1、 C 2: Konstante
T g: Referenztemperatur
α T: Verschiebungsfaktor
Die reduzierte Frequenz f r wird als Produkt aus Verschiebungsfaktor und Messfrequenz ausgedrückt.
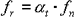
Gleichung 12
Die Beziehung zwischen dem Verschiebungsfaktor (α T : Übertragungskoeffizient) und der WLF-Gleichung ist in Abbildung 2 dargestellt, die Beziehung zwischen Temperatur und Verschiebungsfaktor durch Setzen von C 1 = 17,44, C 2 = 51,6 in der WLF-Gleichung, T g als Parameter ist in gezeigt Figur 3.
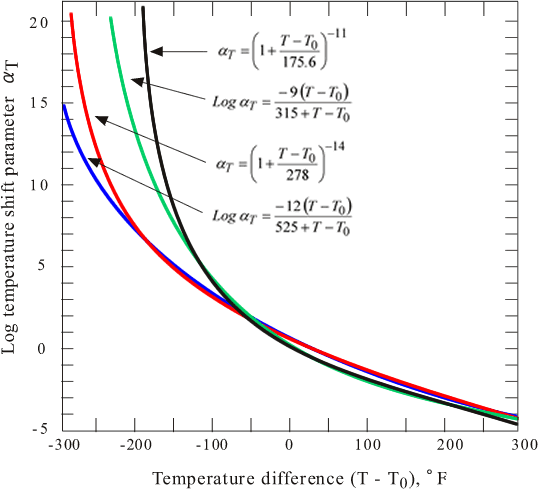
Abbildung 2: Vergleich der Masterkurven
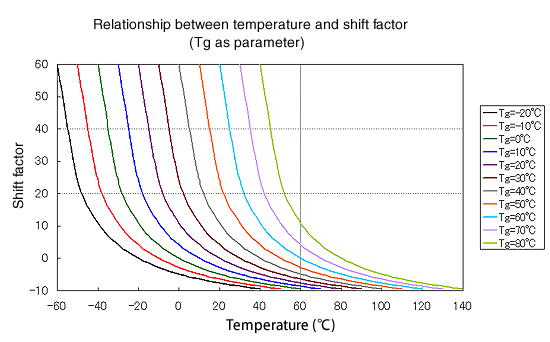
Abbildung 3: Shift-Parameter der WLF-Gleichung
25. Nomogramm der reduzierten Frequenz
Die Messwerte des komplexen Elastizitätsmoduls bei verschiedenen Temperaturen und Frequenzen sind als zusammengesetzte Kurve mit reduzierter Frequenz f r auf der horizontalen Achse und komplexem Elastizitätsmodul auf der linken vertikalen Achse organisiert. Durch Ziehen einer Geraden mit dem Verschiebungsfaktor α T bei der repräsentativen Temperatur …T -2 , T -1 , T 0 , T 1 , T 2… als Proportionalkoeffizient auf der rechten vertikalen Achse in derselben Abbildung können der komplexe Elastizitätsmodul und der Verlustfaktor bei jeder Temperatur [T] und Frequenz [f] direkt aus der zusammengesetzten Kurve abgelesen werden. Die wie oben organisierte Figur wird als reduziertes Frequenznomogramm bezeichnet. Es wird von ISO 10112 als grafische Darstellung des komplexen Elastizitätsmoduls von Dämpfungsmaterialien empfohlen.
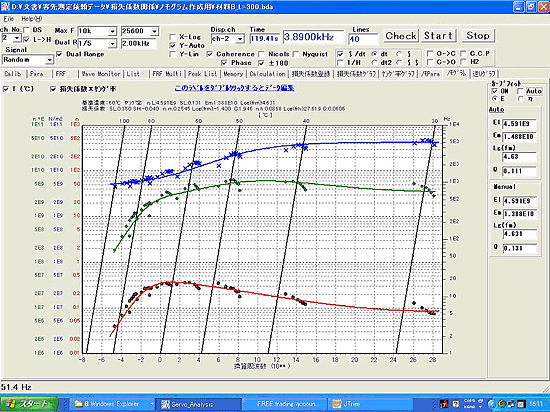
Abbildung 4: Beispiel eines reduzierten Frequenznomogramms
25.1 Erstellen des reduzierten Frequenznomogramms
(1) Entfernung des Einflusses von Grundmaterialien:
Der Verlustfaktor, gemessen an 2 einseitig mit Dämpfungsmaterial befestigten Balkenlagen, ist eine Kenngröße eines Verbundes aus Dämpfungsmaterial und Grundmaterial. Die für die Nomogrammanalyse erforderlichen Eigenschaften eines einzelnen Materials werden durch Entfernen des Einflusses des Basismaterials durch die „RKU-Grundgleichung“ (siehe Berechnung des Elastizitätsmoduls) erhalten.
(2) Anwendung der Temperatur-Frequenz-Überlagerung:
Da die Dämpfungseigenschaften (dynamische Eigenschaften) des Dämpfungsmaterials sowohl von der Temperatur als auch von der Frequenz abhängen, ist eine dreidimensionale Anzeige erforderlich, um den Elastizitätsmodul und den Verlustfaktor für beide Parameter auszudrücken. Dann ist die Temperatur-Frequenz-Überlagerung wirksam. Die Temperatur-Frequenz-Überlagerung ist sehr nützlich für viskoelastische Materialien (insbesondere Glasübergangszustand). Durch Ersetzen der Temperaturänderung durch Frequenz (reduzierte Frequenz) können die dynamischen Eigenschaften des Dämpfungsmaterials in zwei Dimensionen ausgedrückt werden. Wenn die Glasübergangstemperatur T g als Referenztemperatur T 0 genommen wird, wird die WLF-Gleichung als C 1 = 17,44 、 C 2 gesetzt =51,6. Die WLF-Gleichung ist für amorphe Polymere gut vervollständigt. Es ist jedoch nicht für kristalline Moleküle oder Füllstoffe geeignet, da Fehler zunehmen und unterhalb der Glasübergangstemperatur größer werden.
(3) Masterkurve:
Durch Anwenden von Temperatur, Frequenzreduzierungsregel und Kombinieren mehrerer Temperaturdaten zu einer kontinuierlichen Hauptkurve wird das reduzierte Frequenznomogramm vervollständigt, indem der Verlustfaktor und der Elastizitätsmodul des einzelnen Dämpfungsmaterials auf der reduzierten Frequenzachse aufgetragen werden. Um diese komplexe Eigenschaft einfach handhabbar zu machen, ist es auch möglich, das vorab festgelegte viskoelastische Eigenschaftsmodell anzupassen und die viskoelastische Eigenschaft mit mehreren Parametern auszudrücken.
25.2 Verfahren zur Erstellung des Nomogramms
Bei der bestimmten Temperatur (T –2 ~T +2 ) des einzelnen Dämpfungsmaterials, die aus der RKU-Gleichung erhalten wird, ist die Beziehung zwischen Frequenz und Elastizitätsmodul in Abbildung 5, die Beziehung zwischen Frequenz und Verlustfaktor in Abbildung 6 wie unten gezeigt.
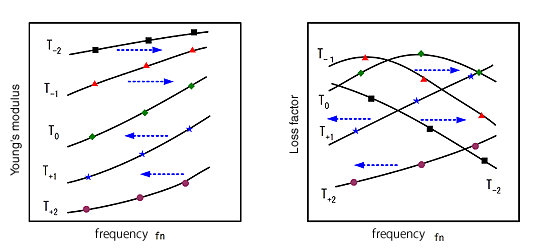
Abbildung 5: Frequenz und Elastizitätsmodul | Abbildung 6: Frequenz und Verlustfaktor
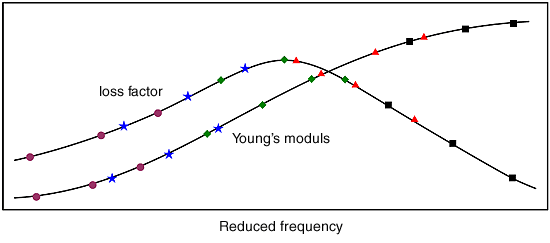
Abbildung 7: Reduzierte Frequenz und Elastizitätsmodul, Verlustfaktor
Dabei wird das in Abbildung 5, 6 gezeigte Temperaturverhalten des viskoelastischen Materials betrachtet. Die Glasübergangstemperatur wird aus diesen Zahlen geeignet abgeschätzt, und die Referenztemperatur (T 0 ) der temperaturreduzierten Frequenzseite wird nahe T g eingestellt .
Bestimmen einer bestimmten Temperatur T 1 (eine Messtemperatur eines Probenbalkens).
- Berechnen Sie α T .
- Multiplizieren Sie die im Experiment gemessene Resonanzfrequenz des Testmusters (bei der Temperatur T 1 ) mit α T , um die reduzierte Frequenz f r zu berechnen .
- Nimmt man die reduzierte Frequenz auf der horizontalen Achse und die dynamischen Eigenschaften des Dämpfungsmaterials allein (Verlustfaktor, Elastizitätsmodul) auf der vertikalen Achse, erhält man einen Teil von 7 bei T 1 .
- Wiederholt man diesen Vorgang für andere Messtemperaturen, T 1 , T 2usw., Fig. 7 ist vervollständigt. Wenn die Anordnung der Daten in dieser Figur nicht glatt ist, ändern Sie die Referenztemperatur T 0 , erstellen Sie FIG. 7 erneut und wiederholen Sie diesen Vorgang, bis die Datenzeichnung glatt angeordnet ist.
- Nimmt man schließlich die (Resonanz-)Frequenz auf der rechten vertikalen Achse und die Temperatur auf der oberen horizontalen Achse, wird das reduzierte Frequenznomogramm vervollständigt.
25.3 Hinweise zur Nomogrammerstellung
Bitte beachten Sie beim Erstellen des Nomogramms Folgendes.
Das Ziel ist ein zweischichtiger Bernulli-Euler-Strahl, erhöhen Sie also nicht das Dickenverhältnis der Probe (innerhalb des Dreifachen). Stellen Sie sicher, dass keine Scherverformung auftritt. Die Gleichung berücksichtigt nicht die Auswirkungen der Dehnung. Da der Verlustfaktor von Eisen und Aluminium kleiner als 0,001 ist, wird der Verlustfaktor des Grundmaterials mit 0 (Null) angenommen.
Der Einfluss von Messfehlern und Materialfehlern nimmt im Berechnungsprozess zu. Bei der Berechnung des Elastizitätsmoduls wird die Frequenz durch das Quadrat beeinflusst, die Dicke wird durch das Quadrat beeinflusst, die Länge wird durch die vierte Potenz beeinflusst.
Insbesondere beim Erhalten des reduzierten Frequenznomogramms können die Messdaten bei einer hohen Temperatur in vielen Fällen nicht verwendet werden. Dies liegt daran, dass, wenn das Nomogramm des Materials erhalten wird, der Quadratwurzelwert des RKU ( 23. Berechnung des Elastizitätsmoduls, Die zweischichtige Verbundplatte, die obere Formel ) sehr klein oder negativ ist. Daher wird α ![]() 1,1 bereitgestellt, um die Berechnungsgenauigkeit sicherzustellen. Basierend auf dieser Beurteilungsbedingung ist es notwendig, die Messdaten beim Erstellen des Nomogramms zurückzuweisen. Eine der Methoden zur Erhöhung von α (Gegenmessung), der Verlustfaktor der Probe sollte möglichst η > 0,01 sein.
1,1 bereitgestellt, um die Berechnungsgenauigkeit sicherzustellen. Basierend auf dieser Beurteilungsbedingung ist es notwendig, die Messdaten beim Erstellen des Nomogramms zurückzuweisen. Eine der Methoden zur Erhöhung von α (Gegenmessung), der Verlustfaktor der Probe sollte möglichst η > 0,01 sein.
25.4 Wie man das Nomogramm der reduzierten Frequenz liest
Hier ist ein Beispiel für das Nomogramm der reduzierten Frequenz in Abbildung 8. Verlustfaktor (η • ), Speichermodul (Young's Modul, E' × ) , Verlustmodul (E” • ) sind die linke vertikale Achse, die Frequenz ist die rechte vertikale Achse. Die reduzierte Frequenz fr ist die untere horizontale Achse, die Temperatur ist die obere horizontale Achse.
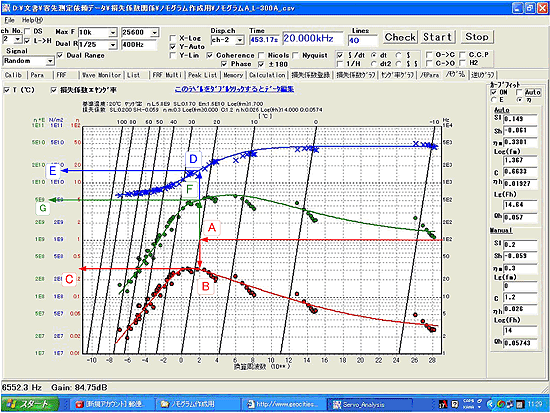
Abbildung 8: Beispiel eines umgewandelten Frequenznomogramms
Hier ist das Verfahren, um den Verlustfaktor und den Elastizitätsmodul des einzelnen Dämpfungsmaterials zu erhalten das Nomogramm in Frequenz 100 Hz, Temperatur 20 ℃. Zeichnen Sie die Linie nach links von 100 Hz auf der rechten vertikalen Achse (Frequenz). Finden Sie den Schnittpunkt A zwischen dieser Linie und der diagonalen Linie von 20 ° C auf der oberen horizontalen Achse (Temperatur). Zeichnen Sie eine Senkrechte vom Schnittpunkt A , um den Schnittpunkt B mit der Kurvenanpassungslinie des Verlustfaktors zu finden , und lesen Sie dann links von B den Wert C auf der linken vertikalen Achse als Verlustfaktor ab, etwa η = 0,3. Zeichnen Sie eine Senkrechte vom Schnittpunkt A , um den Schnittpunkt D mit der Kurvenanpassungslinie des Elastizitätsmoduls zu finden, dann nach links von D, lesen Sie den Wert E auf der linken vertikalen Achse als Verlustfaktor ab, etwa E'=1,8E10 (N/m 2 ), ziehen Sie eine Senkrechte vom Schnittpunkt A , um den Schnittpunkt F mit der Kurvenanpassungslinie des Verlustmoduls zu finden, dann nach links von F , lesen Sie den Wert G auf der linken vertikalen Achse als Verlustmodul ab, etwa E''=5,2E8 (N/m 2 )
26. Umgekehrtes „U“-Diagramm
Wenn die Messdaten des Verlustfaktors mit dem Elastizitätsmodul auf der horizontalen Achse und dem Verlustfaktor auf der vertikalen Achse aufgetragen werden, sind die Daten so angeordnet, als ob der Buchstabe „U“ auf dem Kopf steht. Diese Anordnung ist unabhängig von der Referenztemperatur T 0 gleich . Je besser die Messgenauigkeit des Verlustfaktors ist, desto mehr sind die aufgetragenen Punkte auf der umgekehrten U-Form angeordnet. Da die inverse U-förmige Kurve basierend auf dem Kurvenanpassungsergebnis des Elastizitätsmoduls gezeichnet wird, wird die Korrelation mit den Messdaten (Plot) schlechter, wenn die Kurvenanpassung nicht effizient ist. Das umgekehrte U-förmige Diagramm ist nützlich, um die Genauigkeit der Kurvenanpassung mit dem Elastizitätsmodul und die Messgenauigkeit des Verlustfaktors und der Resonanzfrequenz der Probe zu überprüfen.
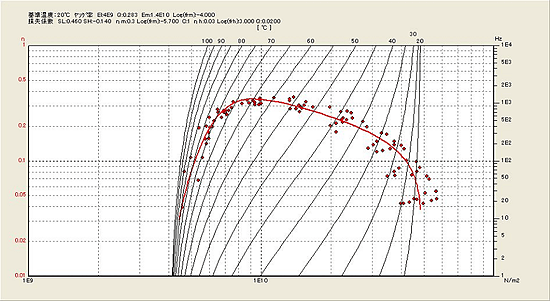
Abbildung 9: Das umgekehrte „U“-Diagramm
27. Näherung des Verlustfaktors
Als Näherungsgleichung, die für den Verlustfaktor und die reduzierte Frequenz charakteristisch ist, wird die Kurvenanpassung in Fig. 10 durchgeführt. Sie wird wie folgt erhalten.
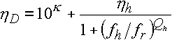
Gleichung 13
Hier ist K:
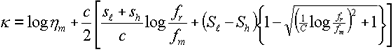
Gleichung 14
|
○ Verlustfaktorparameter (8 Elemente) |
|
|
:Neigung der linken Seite gegen die Spitze des Verlustfaktors |
|
|
:Neigung der rechten Seite gegen die Spitze des Verlustfaktors |
|
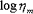 |
:Gewöhnlicher Logarithmus gegen den maximalen Wert des Verlustfaktors |
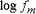 |
:Gemeiner Logarithmus der reduzierten Frequenz mit dem maximalen Wert des Verlustfaktors |
|
c |
:Krümmung |
|
Q h |
:Krümmung der rechten Seite des Verlustfaktors |
|
η h |
:Verlustfaktor bei maximal reduzierter Frequenz |
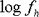 |
:Verringerte Häufigkeit des Krümmungsverlustfaktors auf der rechten Seite |
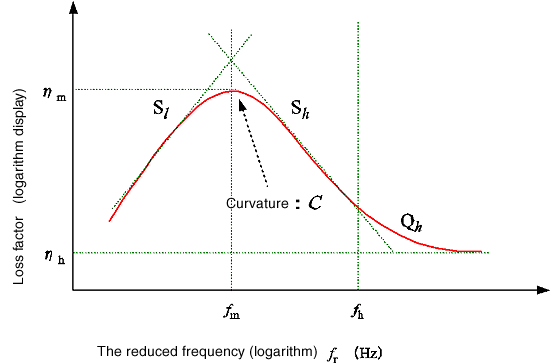
Abbildung 10: Die Näherungsgleichung Kennlinie Verlustfaktor und reduzierte Frequenz
28. Näherung des Elastizitätsmoduls
Als Näherungsgleichung, die für den Elastizitätsmodul bei reduzierter Frequenz charakteristisch ist, wird die Kurvenanpassung in Fig. 11 durchgeführt. Sie wird wie folgt erhalten.
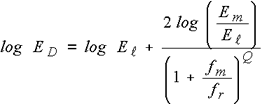
Gleichung 15
○E-Modul-Parameter (4 Elemente)
Q : Neigung in der Mitte des Elastizitätsmoduls
E m : Mittelwert des Elastizitätsmoduls
fm _ : reduzierte Frequenz in der Mitte des Elastizitätsmoduls
El _ : der Elastizitätsmodul bei der minimalen reduzierten Frequenz
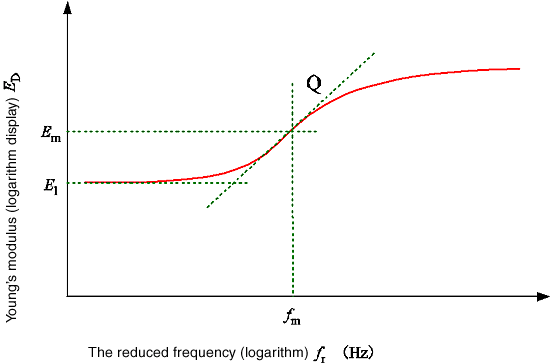
Abbildung 11: Elastizitätsmodul – die Annäherung an die reduzierte Frequenz
Auf diese Weise können durch Bestimmen der Kurvenanpassungsparameter des Verlustkoeffizienten (8 Punkte) und des Elastizitätsmoduls (4 Punkte) der Verlustfaktor und der Elastizitätsmodul durch die Frequenz ohne die Temperatur ausgedrückt werden. Es wird erwartet, dass es auf Simulationssoftware wie die Finite-Elemente-Methode angewendet wird.
29. Messung des Verlustfaktors für die Verformung von Dämpfungslegierungen
Wenn der Verlustfaktor von Dämpfungslegierungen gemessen wird, tritt die Amplitudenabhängigkeit aufgrund des Dämpfungserzeugungsmechanismus auf. Diese Eigenschaft findet man nicht in viskoelastischen Materialien, die nicht durch die Vibrationsamplitude beeinflusst werden. Für diese Messung ist es notwendig, während der zentralen Erregung einen Dehnungsmessstreifen an der Mittelposition anzubringen und eine Grafik mit der Dehnungsamplitude als Parameter zu erstellen. Es ist auch eine effiziente Messung, die Spitzenamplitude (gemessen mit einem Laservibrometer) durch die Dehnungsamplitude an der Mittelposition zu ersetzen, da es mühsam ist, Dehnungsmessstreifen an allen Messproben anzubringen, Problem der S/N-Rate. Das Blockdiagramm ist wie folgt dargestellt:
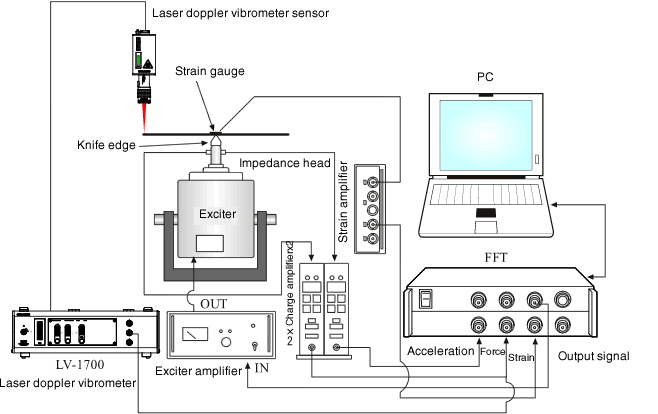
Abbildung 1: Die Systemkonfiguration zur Messung des Verlustfaktors für die Verformung von Dämpfungslegierungen
Das folgende Diagramm zeigt, dass die Linien der Spitzenamplitude zur gleichen mittleren Dehnungsamplitude gezogen werden, selbst wenn die Materialien die gleichen Abmessungen und Dicken, aber unterschiedliche Elastizitätsmoduln (7 Arten von Elastizitätsmoduln) aufweisen.
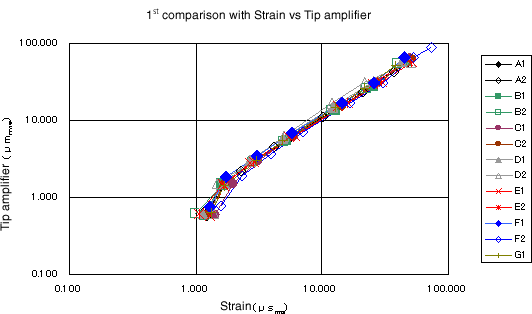
Abbildung 2
Die Messmethode des Verlustfaktors ist eine, die die Amplitude allmählich ändert und aus der mechanischen Impedanz mit der Halbwertsmethode (Amplitudenrate 100: 1) gewinnt, und eine andere, die über Impuls- oder Tonstoßwellen mit Resonanzfrequenz schwingt und daraus gewinnt Dämpfung an der Zeitachse über logarithmisches Dekrement. Die folgenden 2 Zahlen werden aus der zweiten oben erwähnten Methode erhalten.
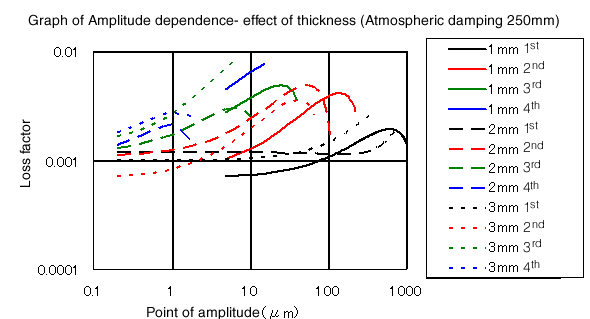
Abbildung 3
Es zeigt, dass es nicht nur auf die Amplitude, sondern auch auf die Materialdicke ankommt. Die Abbildung zeigt einen Materialvergleich.
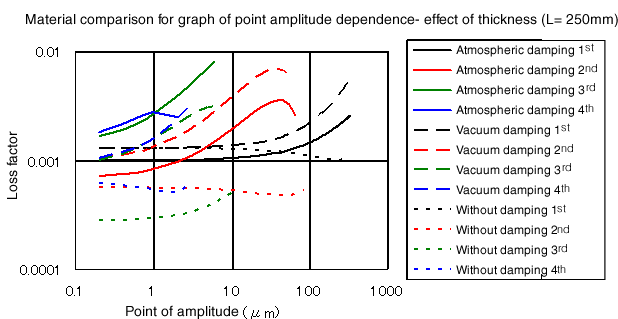
Abbildung 4
Die folgende Abbildung ist ein Diagramm, bei dem die horizontale Achse durch die Dehnungsamplitude ersetzt ist (die Daten unterscheiden sich von der obigen Abbildung).
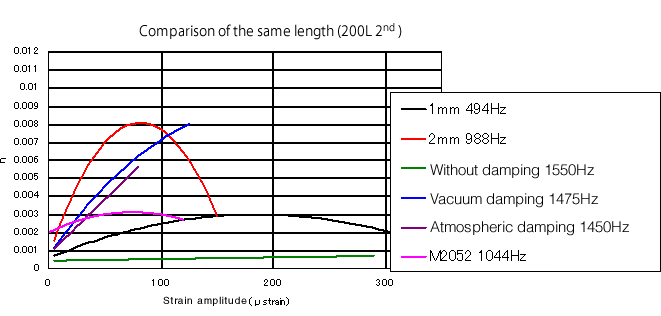
Abbildung 5
Wie in der Abbildung unten gezeigt, ist es einfach, ein Konturdiagramm zu lesen, in dem die Horizontale die Amplitudendehnung, die Vertikale die Frequenz und der Verlustfaktor senkrecht zum Papier (Z-Richtung) ist.
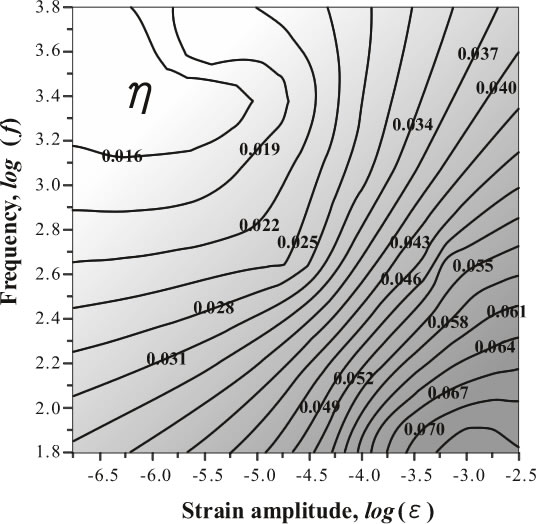
Abbildung 6
30. Referenzen
| 1. | Die Frequenzauflösung und das Zeitfenster des FFT-Analysators bei der Messung des Verlustfaktors von Dämpfungsmaterialien, geschrieben von Mr. Nakazawa, Mr. Inoue, Society of Automotive Engineers of Japan, Inc. |
| 2. | „On the Use of Windows for Harmonic Analysis with the dissrete Fourier Transform“ PROCEEDING OF THE IEEE, VOL66, NO.1, JANUAR 1978 |
| 3. | Kommentare zum charakteristischen Zeitfenster, geschrieben von Kenichi Kido |
| 4. | Vergleich der Messung der Dämpfungseigenschaften (2-lagige Dämpfungsmaterialien), Society of Damping Technology |
| 5. | Studie zur Standardisierung der Messung dynamischer Eigenschaften von Dämpfungsmaterial, Japanischer Maschinenverband, Japan Automobile Research Institute |
| 6. |
Messung, Prüfung, Bewertung der Dämpfungskapazität, geschrieben von Shigeru Inoue |
| 7. |
Handbuch zur Messung des Verlustfaktors, Society of Damping Technology |
| 8. | MLWilliams, RFLandel und JdFerry: J. America. Chem. Soc., 77, 3701, 1955 |
| 9. | ISO 10112 Dämpfungsmaterialien - Grafische Darstellung des komplexen Moduls (15.9.1991) |
| 10. | AdNashif, digJones, JPHenderson: VIBRATION DAMPING, A Wiley – Internationale Veröffentlichung, 1985 |
| 11. | Test und Studie zur Dämpfungskapazität von 2-lagigen Dämpfungsmaterialien, Society of Damping Technology |
31. Ergänzungsmerkmale des elektromagnetischen Erregers (Detektor), der für die Cantilever-Methode verwendet wird
31.1 Impedanzcharakteristik des elektromagnetischen Detektors

Die äußere Form von MP-0910 und M-0912 ist gleich.
Messmethode
Messen Sie mit 2 Arten von elektromagnetischen Detektoren (dC-Widerstandswert: MP-0910- 850 bis 950 Ω, MP-0912- 85 bis 105 Ω). Ein 1-Ω-Zementwiderstand wird in die elektromagnetische Detektorserie eingefügt, der Strom wird erfasst und die Frequenzgangfunktion mit Spannung wird gemessen. Siehe Abbildung 1.
Als Ergebnis ist ersichtlich, dass sich die Impedanz erheblich ändert. MP-910 und MP-912 sind fast parallel. Bei Verwendung des MP-910 ist die Impedanz höher, daher muss auf die Impedanz des angeschlossenen Instruments geachtet werden. Wenn er als elektromagnetischer Erreger verwendet wird, wird erwartet, dass ein normaler Leistungsverstärker eine unzureichende Erregerleistung hat. Es wird angenommen, dass die Impedanz im hohen Bereich aufgrund der Kapazitätskomponenten der Spule abnimmt.
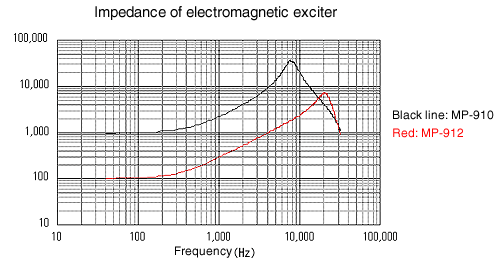
Abbildung 1
31.2 Die Messung der Schwingungsgeschwindigkeitsantwort und Linearität für elektromagnetische Detektoren
Das Messdiagramm ist in Abbildung 2 dargestellt.
Der Schwingungsgeschwindigkeitsverlauf ist in Abbildung 3 dargestellt. (Frequenzgangfunktion mit Laservibrometer) Die Frequenzcharakteristik ist ziemlich flach, dies wird jedoch aufgrund der Sensorleistung auf die Verwendung einer schwachen Montagevorrichtung zurückgeführt (nicht als Erreger verwendet). und keine Reaktionskraft.
Die Linearität in Bezug auf die Schwinggeschwindigkeit ist in den Abbildungen 4 bis 7 dargestellt. Es zeigt sich, dass MP-910 und MP-912 eine ausreichende Leistung für die Messung des Verlustfaktors aufweisen. Die normalisierte Geschwindigkeit ist ein Wert, der durch Normalisieren der von jedem Detektor gemessenen maximalen Ausgangsleistung auf 100 % erhalten wird, da die Ausgangsspannung des Detektors sehr empfindlich auf den Erfassungsabstand von dem Eisenstück reagiert.
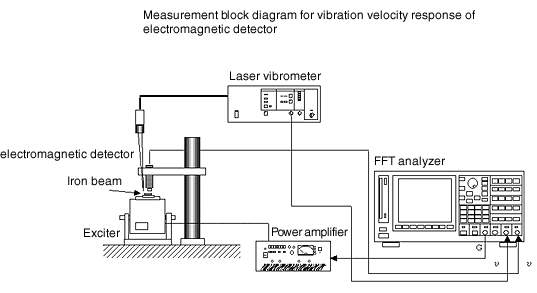
Abbildung 2
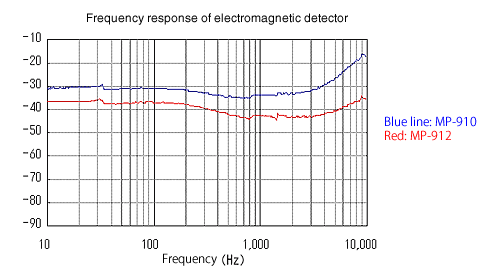
Abbildung 3
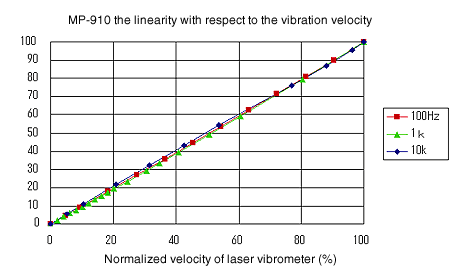
Abbildung 4
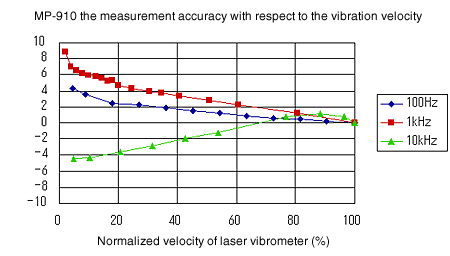
Abbildung 5
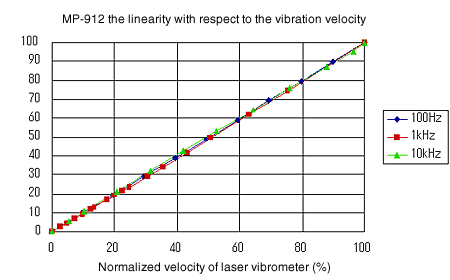
Abbildung 6
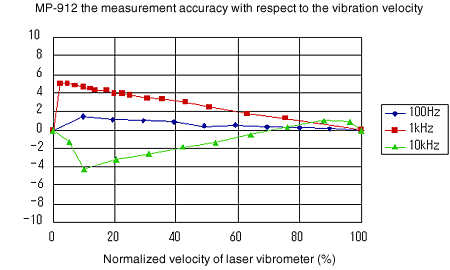
Abbildung 7
31.3 Die Vibrationsgeschwindigkeitsantwort und Linearität für elektromagnetische Detektoren
Das Messdiagramm ist in Abbildung 8 dargestellt
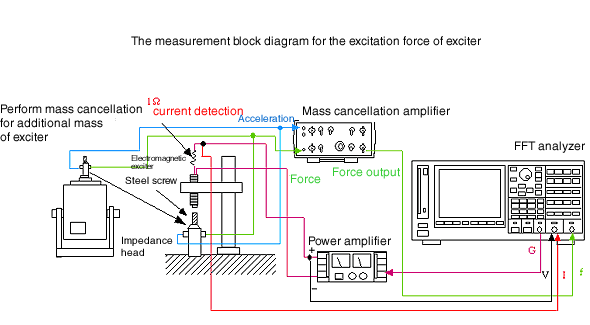
Abbildung 8
Die Massenauslöschung für zusätzliche Masse wird vorher vom Erreger durchgeführt, und das mechanische System wird wie in der Abbildung gezeigt konfiguriert. Verwenden Sie denselben elektromagnetischen Detektor. Messen Sie den Ausgang des Impedanzkopfes, den Strom. Die Anregungskraft ist unterschiedlich, da MP-910, MP-912 unterschiedliche Lücken hat. Normalisieren Sie die horizontale Achse mit dem maximalen Spannungswert. Normalisieren Sie den maximalen Ausgangswert des Impedanzkopfes.
Frequenzcharakteristik
Die beiden Arten der Erregerantwort sind in Abbildung 9 dargestellt, die Stromantwort in Abbildung 10 und die Strom/Kraft-Frequenzantwortfunktion in Abbildung 11. MP-910 mit 1 kΩ Gleichstromwiderstand wird durch seinen eigenen beeinflusst Die Impedanz und ihre Kraftantwort zeigen den Tiefpunkt bei etwa 8 kHz, während die Strom/Kraft-Frequenzantwortfunktion die Spitze zeigt. MP-912 mit 100 Ω DC-Widerstand zeigt relativ einfache Eigenschaften im 10-kHz-Bereich. Es stellt fest, dass die Reaktion des Stroms gegenüber der Spannung des elektromagnetischen Erregers symmetrischer zur Resonanzfrequenz ist als die Eingangsspannung gegenüber der Reaktionsspannung des elektromagnetischen Erregers. (Abbildung 12) Die Anregungskraft kann aus der Abbildung nicht abgelesen werden, da sie normiert ist und, aber die Anregungskraft beträgt etwa 0,05 N/W (att1mmGAP, 1kHz). Um eine praktische Kraft von 0,5 N zu erhalten, benötigt MP-910 etwa 100 V und MP-912 etwa 38 V.
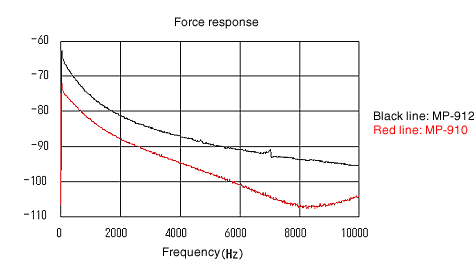
Abbildung 9
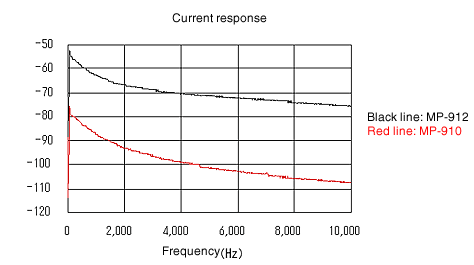
Abbildung 10
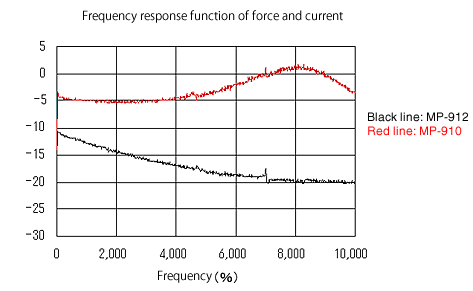
Abbbildung 11
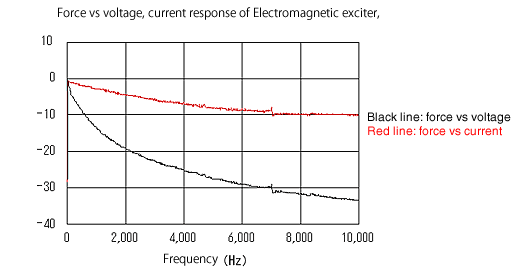
Abbildung 12
Anregungslinearität
Erhöhen Sie allmählich die Spannung zum elektromagnetischen Erreger und messen Sie die Linearität der Erregung. Seine Kennlinien zeigen die Abbildungen 13 bis 16. Er findet sie recht linear.
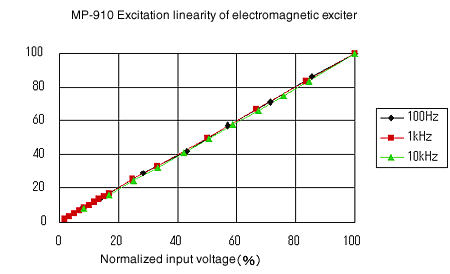
Abbildung 13
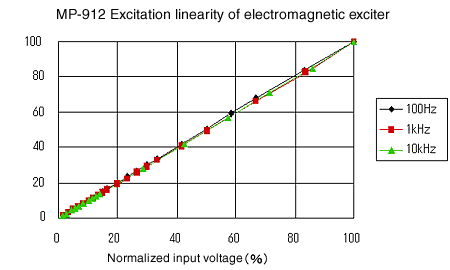
Abbildung 14
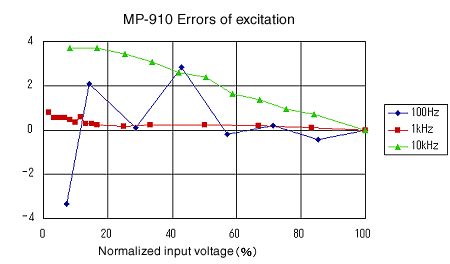
Abbildung 15
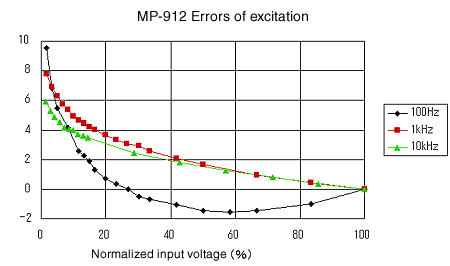
Abbildung 16
31.4 Fazit
Die elektromagnetischen Detektoren/Erreger werden zwar häufig im Cantilever-Verfahren eingesetzt, ihre Eigenschaften wurden jedoch bisher nicht gemessen. Diese Messung erfolgt ausgehend von der Frage, ob die Kraft tatsächlich gemessen wird, um als Quotient in den elektromagnetischen Erreger einzugeben. Als Ergebnis wurde herausgefunden, dass die "Kraft" besser gemessen wird, indem der Eingangsstrom zu dem elektromagnetischen Erreger gemessen wird, anstatt die Spannung zu messen. Die Genauigkeit der Geschwindigkeitserkennung und des Auftretens von Geschwindigkeiten sind höher als erwartet. Wir messen dieses Mal unseren elektromagnetischen Detektor/Erreger und werden die anderer Firmen messen. Als elektromagnetischer Erreger wird wahrscheinlich mehr Erregerkraft erhalten, wenn viele Spulen gewickelt sind, aber dies wird die Impedanz erhöhen und eine nachteilige Wirkung haben. Es ist der beste dicke Draht, der entsprechend oft gewickelt werden sollte (etwa 1000-mal) und der Gleichstromwiderstand sollte mehrere zehn Ω betragen.