Informationen
Was ist dB?
Inhaltsverzeichnis
2. Über Logarithmen
2.1 Was ist ein Exponent?
2.2 Was ist Logarithmus?
2.3 Verschiedene Logarithmen wegen Basisdifferenz
2.4 Spezifischer logarithmischer Wert
3. Was ist Dezibel?
3.1 Definition von Dezibel
3.2 Spezifischer Dezibelwert
3.3 Dezibel repräsentieren den absoluten Wert
3.4 Vorteile der Verwendung von dB
3.5 Dezibel (dB) und Prozent (%)
4. Dezibel in verschiedenen Bereichen
4.1 Elektro-/ Kommunikationssystem
4.2 Akustiksystem
4.3 Vibrationssystem
5. Berechnung des Dezibelwertes
1. Einführung
Dezibel (dB) werden in verschiedenen Bereichen wie Elektrizität, Kommunikation, Optik, Ton, Vibration usw. verwendet. Hier fassen wir die grundlegende Definition von Dezibel (dB), die Bedeutung seiner Verwendung, seine Bequemlichkeit, seine Verwendung in verschiedenen Bereichen und so weiter zusammen.
2. Über Logarithmen
Der Logarithmus wird zur Definition von Dezibel (dB) verwendet. Da das Verstehen der Natur des Logarithmus das Verstehen von db bedeutet, beginnen wir mit einer logarithmischen Erklärung.
Notiz: Dieses Kapitel richtet sich an Personen mit geisteswissenschaftlichem Hintergrund. Bitte überspringen Sie dieses Kapitel, wenn Sie einen naturwissenschaftlichen Hintergrund haben.
2.1 Was ist ein Exponent
Wenn Sie eine große Zahl ausdrücken, wird häufig ein Potenzausdruck verwendet, da die Anzahl der Ziffern zunimmt. Beispielsweise wird eine Zahl von 1 Million als 1 Million = 1.000.000 = 10 6 ausgedrückt .
Wenn es durch eine Potenz von 10 ausgedrückt wird, verringert sich die Anzahl der Stellen und die Berechnung wird vereinfacht. Im Allgemeinen, wenn eine bestimmte Zahl N durch eine Potenz einer willkürlichen positiven Zahl a dargestellt wird:

Gleichung 2.1
Wobei wir sagen, dass N = a m ( a >0, a ≠1) eine Exponentialdarstellung von N ist , a die Basis und m der Exponent ist. Wenn Sie dies verallgemeinern und m sowohl auf reelle Zahlen als auch auf ganze Zahlen erweitern, wird die Exponentialfunktion erhalten.
Wichtige Formeln für Exponenten:

Gleichung 2.2
Gleichung 2.3
2.2 Was ist Logarithmus?
Als nächstes definieren Sie den Logarithmus. In Gleichung (2-1) betrachten wir die Anzahl der Potenzen von a , die N sein werden . Wir nennen m (die Anzahl der Potenzen) den Logarithmus von N und er wird durch den folgenden Ausdruck ausgedrückt.

Gleichung 2.4
Hier bezeichnen wir m als Logarithmus, a als Basis und N als Antilogarithmus. Es ist wichtig zu beachten, dass m je nach Darstellungsmethode manchmal unterschiedlich ausgedrückt wird. Das m in Ausdruck (2-1) und Ausdruck (2-4) ist unterschiedlich, selbst wenn sie beide " m " sind. Die Exponentialfunktion wird zentriert auf N dargestellt , und die Notation, die zentriert auf m dargestellt wird, ist eine logarithmische Funktion. Sie sind Umkehrfunktionen voneinander. In der englischen Grammatik gesprochen, entspricht es einer Beziehung wie aktiv und passiv.
Durch Einsetzen von m in Gleichung (2-4) in Gleichung (2-1) erhalten wir den nachstehenden relationalen Ausdruck.

Gleichung 2.5
Außerdem können wir wie bei der Exponentialformel eine wichtige Formel für Logarithmen erhalten.

Gleichung 2.6

Gleichung 2.7
Es wird gesagt, dass der Logarithmus im sechzehnten Jahrhundert von John Napier und anderen entdeckt wurde, um die Berechnung von Multiplikationen und Potenzierungen zu vereinfachen. Es schien in der Zeit ohne Taschenrechner oder Computer eine sehr nützliche Berechnungsmethode zu sein.
2.3 Verschiedene Logarithmen wegen Basisdifferenz
Welche Art von Wert ist für die Basis a in Gleichung 2.4 angemessen?
Je nach Basis werden folgende Logarithmen verwendet.
Tabelle 1 Verschiedene Logarithmen aufgrund unterschiedlicher Basis
| Basis a | Art des Logarithmus | Anwendungsbereich |
| 10 | Gemeiner Logarithmus | Allgemeine Technische Informatik |
| e (Napier-Konstante) | Natürlicher Logarithmus | Mathematische Analyse |
| 2 | Binärer Logarithmus | Kommunikationstheorie |
Da der dekadische Logarithmus hauptsächlich für Dezibel (dB) verwendet wird, Hauptthema hier, bedeutet der Logarithmus in diesem Bericht den dekadischen Logarithmus. Außerdem ist die Basis a = 10 in Gleichung 2.4 entfällt.
Zum Beispiel: Der Logarithmus von 1 Million ist 6 ⇒ log (1.000.000) = log (10 6 ) = 62.4 Spezifischer logarithmischer Wert
2.4 Spezifischer logarithmischer Wert
Tabelle 3 unten rechts zeigt logarithmische Werte für reelle Zahlen von 1 bis 10. Obwohl es jetzt einfach ist, mit einem Taschenrechner zu berechnen, können einige aus anderen Werten berechnet werden, wie in Tabelle 2 unten.
Tabelle 2 „Beispiel Logarithmuswert“ (Auszug)
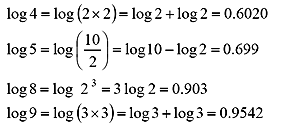
Abbildung 1 zeigt das Diagrammbeispiel des gewöhnlichen Logarithmus y=log(x). Ein numerisches Beispiel, wenn der Antilogarithmus x eine ganze Zahl ist, ist in Tabelle 3 gezeigt. Durch den Wert des Antilogarithmus x;
y < 0 wenn x < 1
y = 0 wenn x = 1
y > 0 wenn x > 1
Das bedeutet, dass ein nachfolgend beschriebener Dezibelwert auch negativ sein kann.
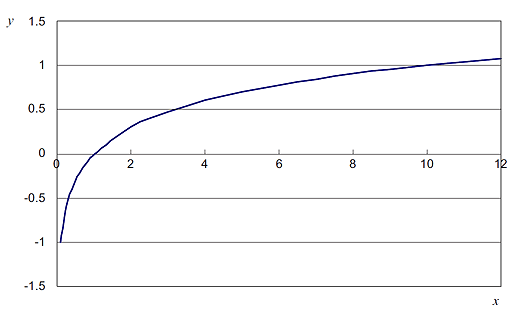
Abbildung 1: Beispiel für eine Grafik mit gewöhnlichem Logarithmus.
Tabelle 3 Beispiel für den Logarithmuswert
| Antilogarithmus | Logarithmen |
| 1 | 0 |
| 2 | 0,301 |
| 3 | 0,4771 |
| 4 | 0,6021 |
| 5 | 0,699 |
| 6 | 0,7782 |
| 7 | 0,8451 |
| 8 | 0,9031 |
| 9 | 0,9542 |
| 10 | 1 |
3. Was ist Dezibel?
3.1 Definition von Dezibel
Das Dezibel wurde zuerst verwendet, um den Grad der Leistungsübertragungsdämpfung (dh das Verhältnis) in einem elektrischen System darzustellen. Nehmen wir nun an, dass 2 elektrische Potenzen P 1 und P 2 sind und das Verhältnis des gemeinsamen Logarithmus x ist , was ist

Gleichung 3.1

Gleichung 3.2
Dieses x wird als Glocke (B) bezeichnet. Dies ist darauf zurückzuführen, dass der US-Amerikaner Alexander Graham Bell es erstmals als Darstellung der Übertragungsdämpfung der Leistung im Telefon verwendete. Da die Glocke (B) selbst zu groß ist, wird üblicherweise Dezibel (dB) verwendet, das 1 Zehntel seines Wertes beträgt.
Notiz: Die „Glocke (B) selbst ist zu groß“ bedeutet, dass der quantitative Wert von 1 Glocke groß, aber numerisch klein ist. Beispielsweise entspricht 7 B 70 dB. Dies ist einfacher zu verstehen, wenn man eine Länge von 1 m und eine Länge von 1 mm vergleicht.
Dezibel L ist definiert als das 10-fache des Logarithmus des elektrischen Leistungsverhältnisses zwischen zwei Punkten (P 1 , P 2 ).

Gleichung 3.3
Obwohl die Definition von dB ursprünglich das elektrische Leistungsverhältnis ist, wird es auf diese Weise auch häufig für das Spannungsverhältnis (oder Stromverhältnis) verwendet. Da die Leistung proportional zum Quadrat der Spannung (oder des Stroms) ist, wird es so

Daher ist ein Dezibel [L] beim Spannungsverhältnis definiert als das 20-fache des Logarithmus des Spannungsverhältnisses zwischen 2 Punkten (V 1 , V 2 ).

Gleichung 3.4
Auf diese Weise wird derselbe Dezibelwert erreicht, unabhängig davon, ob es sich um das Verhältnis der elektrischen Leistung (Leistung) oder das Verhältnis der Spannung (Effektivwert oder linearer Wert) handelt.
Notiz: Physikalische Signale wie Elektrizität und Schall (Vibration) sind normalerweise Wechselstromsignale. Daher wird für die physikalische Größe der Effektivwert verwendet. In diesem Dokument ist die physikalische Größe, die bei der Dezibel-Berechnung verwendet wird, ihr effektiver Wert.
Bei der Berechnung der Übertragungskreistheorie wird manchmal Nepa (Np) verwendet, das natürliche Logarithmen verwendet. Wenn der natürliche Logarithmus als ln dargestellt wird, kann er umgewandelt werden in;

Gleichung 3.5
1 Np entspricht 8,686 dB. Napa stammt von Napier, der den Logarithmus erfunden hat, wie er im vorigen Kapitel 2 beschrieben wird.
3.2 Spezifischer Dezibelwert
Tabelle 4 zeigt die Beziehung zwischen dem üblicherweise verwendeten Dezibelwert und dem Antilogarithmus (Leistungsverhältnis und Spannungsverhältnis). Anhand dieser Tabelle lässt sich leicht der Dezibelwert (Richtwert) für die Spannungsüberhöhung ermitteln
Tabelle 4 Häufig verwendeter Dezibelwert und dessen umgerechneter Wert
| dB-Wert | -20 | -6.02 | 0 | 3.01 | 6.02 | 10 | 20 | 30 | 40 |
| Elektrisches Leistungsverhältnis | 0,01 | 0,25 | 1 | 2 | 4 | 10 | 100 | 1.000 | 10.000 |
| Spannungsverhältnis | 0,1 | 0,5 | 1 | 1.41 | 2 | 3.16 | 10 | 31.6 | 100 |
Zum Beispiel: Wie wäre es mit 5 mal?

3.3 Dezibel repräsentieren den absoluten Wert
Dezibel, wie auch definiert, stellt das Verhältnis der beiden Größen dar, was einfach den relativen Pegelwert bedeutet. Wenn der Referenzwert (der Nenner des Verhältnisses) als feste physikalische Größe definiert ist, kann der Dezibelwert in diesem Fall leicht in den absoluten Wert der physikalischen Größe umgerechnet werden, sodass er als absoluter Pegelwert angesehen werden kann.
Allgemein wird die in Dezibel ausgedrückte Größe der physikalischen Größe im Bereich der Elektrizität und des Schalls (Vibration) als „Pegel (Einheit dB)“ bezeichnet. Von hier aus werden Pegel und Dezibel als fast gleichbedeutend erklärt.
Ein Beispiel zum Ausdrücken eines Spannungswerts wird unten gezeigt. Wenn der Referenzwert des Spannungsverhältnisses als 1 V definiert ist, kann ein beliebiger Spannungswert durch einen Dezibelwert ausgedrückt werden. Die Einheit ist in diesem Fall dBV.
Wenn zum Beispiel x (V) gleich y (dBV) ist;

Gleichung 3.6
Bezugswert 1 können Sie bei der Berechnung weglassen.
Notiz: Wenn im Folgenden der absolute Standardwert 1 ist, dann wird der Wert 1 in der Definitionsformel des absoluten Pegelwerts weggelassen. Das heißt, der Wert des Spannungsverhältnisses in obiger Tabelle 4 kann als Spannungswert betrachtet werden.
Zum Beispiel:
2 V ⇒ 6 dBV
3,16 V ⇒ 10 dBV
Tabelle 5 Spannungsbereich und Dezibel
| Spannungswert (V) | Dezibelwert (dBV) |
| 10 | 20 |
| 3,16 | 10 |
| 1 | 0 |
| 0,316 | -10 |
| 0,1 | -20 |
| 0,0316 | -30 |
| 0,01 | -40 |
Dieser absolute Pegelwert wird verwendet, um den Spannungsbereichswert des Eingangsteils im FFT-Analysator auszudrücken (siehe Tabelle 5).
Das gleiche gilt für andere physikalische Größen. Betrachten wir zum Beispiel ein Beispiel für Schwingungsbeschleunigung. Wenn der Referenzwert auf 1 m/s 2 definiert ist , dann bedeutet 5 m/s 2 etwa 14 dBm/s 2 . Im bisherigen Beispiel war der Referenzwert 1, also war die Berechnung einfach. Der in der Akustik häufig verwendete Referenzwert des Schalldruckpegels ist jedoch nicht 1. Auch hier drückt der Dezibelwert in gleicher Weise den Absolutwert (Schalldruckwert) aus.
Dies wird später beschrieben. Das Dezibel selbst ist keine Einheit von SI-Einheitensystemen, aber in der Akustik wird Dezibel als einheitenkonforme Größe verwendet.
Zusammenfassend lässt sich sagen, dass der absolute Pegelwert die physikalische Größe selbst darstellt, wenn man dB als Einheit betrachtet. Es gibt also viele Fälle, in denen es als „dB ○ ○“ statt einfach als „dB“ geschrieben wird.
3.4 Vorteile der Verwendung von dB
Wie Sie den bisherigen Erläuterungen entnehmen können, bietet die Verwendung von Dezibel viele Vorteile. Das Folgende ist ein typischer Grund.
- Wenn Sie große Zahlen ausdrücken, wie z. B. die Verstärkung des Verstärkers, kann die Verwendung von Dezibel diese mit weniger Stellen ausdrücken. Beispielsweise sind 50.000 Mal 94 dB.
- Wenn eine Kennlinienauswertung durchgeführt wird, wie z. B. bei einem mehrstufigen Verstärker oder einer Vielzahl von Übertragungssystemen, kann die Berechnung einfach durchgeführt werden, da Multiplikation und Division durch Addition und Subtraktion ersetzt werden können.
- Weber-Fechner-Gesetz "Die empfundene Intensität ist proportional zum Logarithmus des Reizes. ", das sich zur Bewertung sensorischer Werte (insbesondere der Akustik) eignet.
3.5 Dezibel (dB) und Prozent (%)
Dezibel und Prozentangaben (Prozent,%) stellen ebenfalls Verhältnisse dar, gegenseitige Umrechnung von Zahlen ist möglich. Das Dezibel wird in diesem Fall normalerweise als Spannungsverhältnis betrachtet. Zum Beispiel sind 10 % -20 dB von 20 log (10/100) = - 20. Beim Ausdrücken des Widerstandstoleranzfehlers und der Toleranz des Frequenzcharakteristikbereichs des Sensors kann er als Verhältnis von einem Referenzwert wie etwa ±5 % ausgedrückt werden. Diese Zahl kann auch in Dezibelwerte umgerechnet werden.
Zum Beispiel ist +10 % (1 + 10/100) mal, entspricht also 0,83 dB, aus 20 log (1,1) = 0,83. Ähnlich entspricht -10 % 20 log (0,9) = -0,92 und -0,92 dB.
Beachten Sie hier, dass % linear und dB logarithmisch ist.
+1 dB ⇒ +12,2 %
-1 dB ⇒ -10,9 %
Gleichungen wie die obigen werden aufgestellt. Wenn es logarithmisch gleich beabstandet ist, ist das lineare Intervall auf der +-Seite breiter. Ganz grob gesagt entspricht ±1 dB etwa ±10 %.
4. Dezibel in verschiedenen Bereichen
Hier werden konkret beschrieben, wie Dezibel in verschiedenen Bereichen verwendet werden.
4.1 Elektro-/ Kommunikationssystem
Dezibel des relativen Pegelwerts werden häufig für die Verstärkung und Dämpfung des Übertragungssystems verwendet. Da die normale Spannungsmessung einfacher ist, errechnet man das Dezibel, indem man das Spannungsverhältnis in die Berechnung der Übertragungskennlinie inklusive Verstärker oder Filter einbezieht.
Wenn beispielsweise ein Signal von 1 mV in eine Schaltung eingegeben wird, wird an diesem Ausgang eine Spannung von 10 V erzeugt. Da in diesem Fall der Spannungsverstärkungsfaktor das 10.000-fache beträgt, beträgt die "Verstärkung 80 dB" unter Verwendung der Gleichung 3.4.
Im Folgenden werden die Dezibel eingeführt, die häufig in Elektro- und Kommunikationssystemen verwendet werden.
dBM
Im Bereich der Leistungsverstärkung wird häufig dBm verwendet . Diese Einheit ist der absolute Pegelwert der elektrischen Leistung, und der Wert von 1 mW wird als 0 dBm definiert.
Wie werden beispielsweise 10 W in dBm ausgedrückt? Da in diesem Fall 10 W gleich 10 4 mW sind, sind es 40 dBm (= 10 log (10 4 )). Wie werden 0,1 mW in dBm ausgedrückt? Da in diesem Fall 0,1 mW 10 –1 mW sind, sind es –10 dBm. Obwohl dBm ursprünglich eine Einheit der elektrischen Leistung ist, wird es im Übertragungssystem auch als absoluter Pegelwert der Spannung verwendet, indem die Impedanz festgelegt wird. Unter der Annahme, dass der Spannungswert von 0 dBm (1 mW) V ist, wenn das Impedanzsystem Z (Ω) ist, wird die Beziehung des Ausdrucks wie folgt erhalten.

Gleichung 4.1
Die Tabelle 6 zeigt Beispiele von Spannungswerten für 0 dBm bei verschiedenen Impedanzwerten aus Gleichung 4.1.
Tabelle 6 Spannungswert für 0 dBm
| Impedanz Z (Ω) | Spannungswert (V) | Das Feld oft verwendet |
| 50 | 0,224 | Drahtloses System |
| 75 | 0,274 | Videosystem |
| 600 | 0,775 | Telefon-Akustiksystem |
Eine Korrelationsformel zwischen dem Spannungswert V und dem Dezibelwert X(dBm)

Gleichung 4.2
Gleichung 4.3
(Beispiel 1) 0,5 V ist 7,0 dBm bei 50 Ω
(Beispiel 2) 1 V ist 11,2 dBm bei 75 Ω
(Beispiel 3) 6 dBm ist 1,55 V bei 600 Ω
dBV, dBμ
Dies sind die absoluten Pegelwerte der elektrischen Leistung, und der Wert von 1 V wird als 0 dBV definiert, und 1 μV wird als 0 dBμ definiert.
Notiz: Grundsätzlich ist der zu nivellierende Spannungswert (Antilogarithmus) der Effektivwert des Signals. dBV wird häufig für Niederfrequenzbandinstrumente wie FFT-Analysatoren verwendet. Im FFT-Analysator ist die Eingangseinheit standardmäßig Spannung (V). Wenn also keine Kalibrierung der physikalischen Größe vorgenommen wird, ist die vertikale Achseneinheit des Leistungsspektrums die Notation [dBV]. Außerdem beträgt der Eingangsspannungsbereich normalerweise 10-dBV-Schritte. Für den Eingangsbereich der Data Station der DS-3000-Serie entspricht beispielsweise die Spannung 1 Vrms einer Spannung von 0 dBV (siehe Tabelle 7).
Tabelle 7 Eingangsbereiche der DS-3000-Serie
| dBV | Vrms | V (Spitze) |
| 20 | 10 | ±14.14 |
| 10 | 3.162 | ±4,471 |
| 0 | 1 | ±1,414 |
| -10 | 0,3162 | ±0,4471 |
| -20 | 0,1 | ±0,1414 |
| -30 | 31,62 m | ±44,71 m |
| -40 | 10 m | ±14,14 m |
Eine Korrelationsgleichung zwischen dem Spannungswert V und dem Dezibelwert X(dBV)
 Gleichung 4.4
Gleichung 4.4
 Gleichung 4.5
Gleichung 4.5
dBμ wird häufig für drahtlose Kommunikation verwendet und basiert auf dem Spannungswert von 1 μV. Obwohl es ursprünglich als dBμV ausgedrückt werden sollte, wird V oft weggelassen.
dBμV/m
Diese Einheit wird verwendet, um den Wert der elektrischen Feldstärke darzustellen, der den Strahlungsemissionswert ausdrückt, z. B. EMV. 1 μV/m ist als 0 dB definiert.
dBc
Dies ist ein relativer Pegelwert der Oberwelle basierend auf der Grundwelle („c“ des Trägers) oder Rauschkomponenten, der bei der Bewertung der spektralen Eigenschaften von Hochfrequenzen und OP-Verstärkern verwendet wird. Wenn beispielsweise die Oberwelle –40 dBm beträgt und die Grundwelle 10 dBm beträgt, beträgt ihre Oberwelle –50 dBc. Diese Beziehung ist die gleiche, selbst wenn die vertikale Achse des Spektrums dBV darstellt. Es wird als Parameter zur Bewertung geringer Verzerrungen wie z. B. eines OP-Verstärkers verwendet.
dBV/√Hz
Bei der Messung des Eigenrauschverhaltens eines Verstärkers wird die spektrale Leistungsdichte (PSD) zur Bewertung herangezogen, da diese vertikale Achse aber ein Effektivwert pro Frequenzeinheit (1 Hz) ist, lautet die Einheit V 2 / Hz oder V/√Hz. Dieser Wert wird in Dezibel als dBV/√Hz ausgedrückt.
4.2 Akustiksystem
Um die Stärke (Größe) von Schall zu quantifizieren, wird üblicherweise auch Dezibel (dB) verwendet. Der Hauptgrund ist, dass wir einen sehr großen Bereich der Schallstärke (Größe) fühlen können und dass dieses Gefühl logarithmisch ist (siehe (3) in 3.4). Die Quantifizierung der Lautstärke wird oft als absoluter Pegelwert in Dezibel (dB) ausgedrückt.
Schalldruckpegel [ L p ]
Schall, der sich in der Luft ausbreitet, ist eine winzige Druckschwankung (Welle), deren Mittelpunkt der atmosphärische Druck (statischer Druck) ist. Der Effektivwert der schwankenden Komponente wird Schalldruck genannt, und Pa (Pascal) ist diese Einheit. Wie oben erwähnt, liegt der Schalldruck, den Menschen normalerweise hören können, im Bereich von 20 μPa bis 20 Pa, ein sehr breiter Wertebereich 10 6 .
Der Schalldruckpegel wird durch die folgende Formel definiert.

Gleichung 4.6
Notiz: Der Schalldruckpegel ist die Stärke (Größe) des physikalischen Schalls. Auf dem Gebiet der Schallmessung wird häufig der Pegel mit der Frequenzbewertung A verwendet, der auf der Grundlage menschlicher Höreigenschaften festgelegt wird, und insbesondere wird er als A-Bewertungs-Schalldruckpegel (allgemein der Geräuschpegel) bezeichnet. Sie wird durch den folgenden Ausdruck definiert.

Gleichung 4.7
Exponentieller Durchschnitt
Bei diesem Verfahren wird der quadratische Wert des momentanen Schalldrucks mit einem bestimmten Zeitgewicht τ exponentiell gemittelt und der Effektivwert zu diesem Zeitpunkt (momentan) erhalten. Der mit dieser Methode erhaltene Dezibelwert ist ebenfalls eine Funktion der Zeit. Dem entspricht der sogenannte Momentanschalldruckpegel, der üblicherweise alle 1 Sekunde auf dem Schallpegelmesser angezeigt wird. Im JIS-Standard (JISC 1509) des Schallpegelmessers wird er Schallpegel mit Zeitbewertung genannt. Im Bereich der akustischen Messung werden oft Fast (0,125 s) und Slow (1 s) für die Zeitbewertung τ (Zeitkonstante) verwendet.
Linearer Durchschnitt
Bei diesem Verfahren wird der quadratische Wert des momentanen Schalldrucks zu einem bestimmten Messzeitpunkt T integriert (gleichgewichtet) und anschließend zum Effektivwert gemittelt. Der daraus zu ermittelnde Dezibelwert ist der repräsentative Wert zu diesem Messzeitpunkt (ein Wert). Im JIS-Standard (JIS C1509) des Schallpegelmessers wird er als zeitgemittelter Schallpegel (äquivalenter Schallpegel) bezeichnet. Wenn die Frequenzgewichtung [A] ist, wird sie zu einem „äquivalenten Geräuschpegel“ im Umgebungsgeräuschfeld.
Schallstärkepegel (Schallintensität) [ L I ]
Schallintensität ist die Energie, die durch eine Einheitsfläche von Schallwellen geht, die sich in einem Medium wie Luft innerhalb einer Zeiteinheit ausbreiten.
Die Einheit ist [W/m 2 ].
Der Schallintensitätspegel wird durch den folgenden Ausdruck definiert.

Gleichung 4.8
Schallleistungspegel [ L W ]
Eine Schallwelle, die sich in einem Medium ausbreitet, kann man sich als Energiefluss vorstellen, und diese Energie wird Schallenergie genannt. Als Betrag, der die Größe dieser Schallenergie darstellt, wird die Schallenergie, die in einer Zeiteinheit durch eine bestimmte Ebene geht, als "Schallleistung" [ P (W)] bezeichnet. Der Schallleistungspegel wird durch den folgenden Ausdruck definiert.

Gleichung 4.9
Die Schallleistung wird hauptsächlich verwendet, um die Größe der von der Schallquelle abgestrahlten Schallenergie auszudrücken. Innerhalb eines bestimmten Frequenzbandes wird die von der Schallquelle pro Zeiteinheit abgestrahlte Gesamtschallenergie als „Schallleistung (Schallleistung der Schallquelle)“ [ P (W)] und ihr Schallleistungspegel als „Schallleistungspegel ( Schallleistungspegel der Schallquelle ) "[ L W ](dB).
Schallenergiepegel [ L J ]
Für den nachhaltig erzeugten Schall wird der obige Schallleistungspegel als Bewertungsmethode verwendet. Für One-Shot- oder Transient-Sound ist es notwendig, mit Energie zu evaluieren. Der Schallenergiepegel [ L J ] wird durch die folgende Gleichung definiert.

Gleichung 4.10
4.3 Vibrationssystem
Absolute Dezibelwerte werden häufig im Bereich der Vibrationssysteme verwendet, insbesondere im Bereich der menschlichen Körpervibration, wie dem akustischen System.
Schwingungsbeschleunigungspegel [ L Va ]
Üblicherweise wird das Beschleunigungssignal als Maß der Schwingung verwendet. Die tatsächliche Vibration ist keine einfache Wellenform wie eine Sinuswelle, sondern ein kompliziertes Signal mit verschiedenen Frequenzkomponenten, sodass ihre Größe durch effektive Werte ausgedrückt wird, die Energie und Leistung entsprechen. Der Schwingungsbeschleunigungspegel [ L Va ] wird durch die folgende Formel definiert.

Gleichung 4.11
Der Referenzbeschleunigungswert ist 10 -5 m/s 2 in JIS, aber 10 -6 m/s 2 ist die Referenz in ISO. Das heißt, eine Differenz von 20 dB im Schwingungsbeschleunigungspegel.
Zum Beispiel: Beispielsweise wird die praktische Einheit "Gal" im seismischen Bereich verwendet. 1 Gal ist 1 cm/s 2 , also entspricht 1 Gal 60 dB für JIS und 80 dB für ISO.
Notiz: Energie ist integraler Bestandteil der Kraft. Als Einheit hat es die Dimension (Leistung) × (Zeit). Umgekehrt entspricht Leistung der Energie pro Zeiteinheit. Beispielsweise ist im Bereich der Elektrizität Strom Leistung und seine Einheit ist kW, die Strommenge ist Energie und seine Einheit ist kWh.
Vibrationspegel [ L V ]
Der Vibrationspegel ist der Pegelwert des Effektivwerts der Vibrationsbeschleunigung, der korrigiert wurde, um ihn dem menschlichen Vibrationsempfinden nahe zu bringen. Der Einfluss von Vibrationen auf den menschlichen Körper hängt von Amplitude und Frequenz ab, und wie sich die Vibration anfühlt, unterscheidet sich in vertikaler und horizontaler Richtung. Dies ist in JIS C 1510-1995 als „Gesamtfrequenzgang der vibrationssensorischen Eigenschaften “ festgelegt. Der Vibrationspegel [ L V ] wird durch die folgende Formel definiert.

Gleichung 4.12
Der Vibrationspegel ist ein Dezibelwert, der dem A-gewichteten Schalldruckpegel (Geräuschpegel) im Soundsystem entspricht.
Notiz: Wie beim akustischen System wird der Effektivwert durch Anwendung der Mittelwertmethode ermittelt, wie unten gezeigt.
Exponentielle Mittelung
Bei diesem Verfahren wird der quadratische Wert des momentanen Schalldrucks mit einem bestimmten Zeitgewicht τ exponentiell gemittelt und man erhält den Effektivwert zu diesem Zeitpunkt (Momentan). Der mit dieser Methode erhaltene Dezibelwert ist ebenfalls eine Funktion der Zeit. Dem entspricht der sogenannte Momentanschalldruckpegel, der üblicherweise alle 1 Sekunde vom Vibrationspegelmesser angezeigt wird.
Im JIS-Standard (JIS C 1510-1995) des Vibrationspegelmessers beträgt die Zeitgewichtung τ (Zeitkonstante, dynamische Eigenschaften) 0,63 s.
Lineare Mittelung
Bei diesem Verfahren wird der quadratische Wert des momentanen Schalldrucks zu einem bestimmten Messzeitpunkt T integriert (gleichgewichtet) und anschließend zum Effektivwert gemittelt. Der daraus zu ermittelnde Dezibelwert ist der repräsentative Wert zu diesem Messzeitpunkt (ein Wert). Dieser Wert wird Äquivalenter Vibrationspegel ( L Veq ) genannt, da die gleiche Bedeutung für das Soundsystem besteht.
5. Berechnung des Dezibelwertes
Wie wir erklärt haben, gibt es bei Dezibel-Werten relative Pegelwerte und absolute Pegelwerte. Wie addieren oder subtrahieren wir diese Werte? Mögliche Kombinationen sind wie folgt.
Relativer Pegelwert und relativer Pegelwert
In diesem Fall können Sie den Dezibelwert einfach addieren oder subtrahieren.
Zum Beispiel: Der kombinierte Verstärkungsfaktor von A-dB-Verstärker und B-dB-Verstärker ist (A + B) dB.
Absoluter Pegelwert und relativer Pegelwert
Auch hier können Dezibelwerte numerisch addiert und subtrahiert werden.
Zum Beispiel: Bei der Messung eines Schalldrucks von 1 Pa (Schalldruckpegel 94 dB) mit einer Empfindlichkeit von -30 dB (bez. 1 V/Pa) Mikrofon und einer Einfügungsdämpfung von -2 dB Vorverstärker ergibt sich eine Spannung von -32 dBV (ca. 25 mV) ausgegeben.
Absoluter Pegelwert und absoluter Pegelwert
In diesem Fall kann die numerische Addition/Subtraktion des Dezibelwerts nicht einfach durchgeführt werden. Unabhängig vom elektrischen System/akustischen Vibrationssystem ist eine Addition/Subtraktion des Leistungswerts erforderlich. Das heißt, geben Sie den Dezibelwert in einen Antilogarithmus zurück, führen Sie eine Addition und Subtraktion mit einem Antilogarithmus durch und wandeln Sie ihn dann in einen Dezibelwert um. Eine solche Addition wird als Energieaddition (Leistungsaddition, Dezibelintegration) usw. bezeichnet.
Beispielsweise wird der Additionswert L dB (oder Subtraktionswert) des absoluten Pegelwerts von L 1 dB und L 2 dB wie folgt berechnet.

Gleichung 5.1
Obwohl die Addition von absoluten Pegelwerten wenig aussagekräftig ist, da die Subtraktion dem Verhältnis des Antilogarithmus entspricht, ist die Differenz in absoluten Dezibel bei gleichem Referenzwert als relativer Dezibelwert aussagekräftig. Zum Beispiel wird die Schalldruckpegeldifferenz zwischen Räumen D, die oft in der akustischen Leistung von Gebäuden verwendet wird, wie folgt als Differenz in Dezibel erhalten.

Gleichung 5.2
Zum Beispiel: Der Schalldruckpegelwert der Zusammensetzung von 60 dB und 63 dB wird durch Einsetzen in Gleichung (5-1) wie folgt erhalten.


Bei einer 1/3-Oktavband-Filteranalyse bei 72 dB bei 800 Hz, 76 dB bei 1 kHz und 74 dB bei 1,25 kHz ist der Pegel der 1/1-Oktavband-Filteranalyse bei der Mittenfrequenz 1 kHz durch Bandsynthese der folgende.

Notiz: Das Verfahren des Addierens und Mittelns des Antilogarithmus wird auch verwendet, um den Mittelwert des absoluten Pegelwerts zu erhalten. Ein solcher Mittelwert wird als Energiemittelwert (Leistungsmittelwert, Dezibelmittelwert) bezeichnet. Beispielsweise beträgt der mittlere Schalldruckpegel L dB der Schalldruckpegel L 1 dB, L 2 dB, L 3 dB:

Gleichung 5.3
Beispielsweise wird der Durchschnittspegel von 80 dB, 82 dB und 84 dB durch Einsetzen in Gleichung (5-3) zu 82,3 dB erhalten. Abhängig von bestehenden Standards kann er jedoch durch den numerischen Durchschnitt der Dezibelwerte erhalten werden. Diese Methode wird manchmal als arithmetisches Mittel der Dezibelwerte bezeichnet.

6. Referenzen und Nachweise
- Ito Kenichi, „Dezibel-Story“: Nikkan Kogyo Shinbun, Ltd. (geschrieben auf Japanisch)
- Sakai Hiroshi und Suzuki Shusaku „Dezibel – Umgang mit der Übertragungslautstärke“: Nikkkan Kogyo Shinbun, Ltd. (geschrieben auf Japanisch)
- Kuno Kazuhiro „dB-Betrachtung“: The Acoustical Society of Japan, Technical Committees on Noise and Vibration (geschrieben auf Japanisch)
- Matsuura Hiroyuki „Various dB“: Nikkei Electronics (geschrieben auf Japanisch)
- „Was ist ein Schallpegelmesser ?" Technischer Bericht der Ono Sokki-Website

