Informationen
Koeffizienten, die Dämpfungseigenschaften darstellen
Inhaltsverzeichnis
2. Koeffizienten, die Dämpfungseigenschaften darstellen
2.1 Logarithmisches Dekrement δ
2.2 Berechnung des logarithmischen Dekrements und des Dämpfungsverhältnisses durch Hilbert-Transformation
2.3 Berechnung des Dämpfungsverhältnisses durch Halbbandbreitenmethode
3. Dämpfungswirkung
3.1 Dämpfungswirkung bei freier Schwingung
3.2 Dämpfungswirkung bei stationärer Schwingung
3.3 Dämpfungswirkung bei transienter Schwingung
4. Zusammenfassung des relationalen Ausdrucks
5. Fazit
5.1 ⟨Ergänzung⟩ Berechnungsverfahren der Halbbandbreitenmethode
5.2 (Referenz) Dämpfungsrate für Struktur und Maschine (Referenzmaterialien)
1. Einleitung
Vibrationen sind ein unvermeidbares Phänomen, wenn die Maschine arbeitet. Vibrationen sind nicht nur unangenehm, sondern auch Störungsursache und führen zum Ausfall der Maschine. Es ist wichtig, Vibrationen im Voraus bei der Konstruktion von Maschinen gründlich zu berücksichtigen und Maßnahmen zu ergreifen, um Vibrationen nicht zu erzeugen oder zu reduzieren, da es Zeit und Kosten kostet, Maßnahmen zu ergreifen, sobald Vibrationen auftreten. Die Schwingungsmessungen sind für Gebäude und Brücken unverzichtbar.
Es gibt 4 Hauptmaßnahmen:
1. Unterbrechen Sie die Vibrationsquelle
2. Entwerfen Sie eine Struktur, die nicht leicht vibriert
3. Dämpfung hinzufügen
4. Schwingungen entgegenwirken
Dieser Artikel konzentriert sich auf „Dämpfung“ und erklärt, wie man die Koeffizienten wie Dämpfungsverhältnis, logarithmisches Dekrement und Q-Faktor erhält und wie sich die Koeffizienten auf das Phänomen der Vibration auswirken.
2. Koeffizienten, die Dämpfungseigenschaften darstellen
Koeffizienten, die Dämpfungseigenschaften darstellen, wie z. B. Schwingungsdämpfung und Dämpfungsmaterialien, umfassen das Dämpfungsverhältnis (Dämpfungsfaktor), das logarithmische Dekrement, den Verlustfaktor und den Q-Faktor. Die Definition und physikalische Bedeutung jedes Koeffizienten wird später erklärt, und dann werden wir zuerst erklären, wie man diese Koeffizienten erhält.
2.1 Logarithmisches Dekrement δ
Im Allgemeinen wird die Amplitude der gedämpften freien Schwingungswellenform exponentiell gedämpft, wie in Abbildung 1 gezeigt. Wenn man den Logarithmus des angrenzenden Amplitudenverhältnisses nimmt, ist es immer ein konstanter Wert. Der natürliche Logarithmus dieses benachbarten Amplitudenverhältnisses wird als logarithmisches Dekrement bezeichnet, das weithin als einfacher Koeffizient verwendet wird, der Dämpfungseigenschaften darstellt. Das Dämpfungsverhältnis, der Verlustfaktor, die physikalisch charakteristische Werte sind, werden durch das logarithmische Dekrement berechnet.

Abbildung 1: Das logarithmische Dekrement
Unter der Annahme, dass die n -te Amplitude zum Zeitpunkt t n an ist und die n + 1, ... n + m -te Amplitude an n + 1 , ... an + m ist, wird das logarithmische Dekrement δ als die folgende Gleichung definiert.

Wenn die Genauigkeit in einem Zyklus nicht ausreicht, rechnen Sie mit m Zyklus.

denn

Das Dämpfungsverhältnis ζ und der Verlustfaktor η werden durch δ berechnet.

2.2 Berechnung des logarithmischen Dekrements und des Dämpfungsverhältnisses durch Hilbert-Transformation
Das logarithmische Dekrement und das Dämpfungsverhältnis werden durch die Hilbert-Transformationsfunktion des FFT-Analyzers erhalten. Die Dämpfungswellenform von Abb. 1 wird in den FFT-Analysator als Zeitachsenwellenform übernommen, durch Ausführen einer Hilbert-Transformation in eine Hüllkurve der Amplitude umgewandelt, und die Y-Achse wird als dB angezeigt, eine gerade Linie mit einer Abwärtsneigung, wie in gezeigt Abb. 2 wird erhalten.

Abbildung 2: Die Berechnung durch Hilbert-Transformation
Unter Verwendung des Δ - Cursors werden Δ X und Δ Y zwischen den zwei Punkten dieser geraden Linie erhalten, und Sie können das logarithmische Dekrement δ und das Dämpfungsverhältnis ζ unter Verwendung der folgenden Gleichung berechnen. Wenn die Vibrationsfrequenz f d ist,

( f d , wird aus dem Frequenzspektrum erhalten. Das Dämpfungsverhältnis ζ kann von einigen Analysatoren automatisch berechnet werden.)
2.3 Berechnung des Dämpfungsverhältnisses nach Halbbandbreitenmethode
Wie später erwähnt wird, zeigt das Schwingungssystem Resonanzeigenschaften, wenn das Dämpfungsverhältnis ζ klein ist. Das Dämpfungsverhältnis, der Verlustfaktor und der Q - Wert können aus den Frequenz-/Amplitudeneigenschaften nahe der Resonanzfrequenz berechnet werden.

Abbildung 3: Methode mit halber Bandbreite
In den in Fig. 3 gezeigten Frequenz-/Amplitudencharakteristiken werden unter Verwendung der Spitzenfrequenz f 0 der Amplitude und der Frequenzbreite Δf bei 3 dB unter dem Spitzenwert der Q-Wert, der Verlustfaktor η und das Dämpfungsverhältnis ζ erhalten durch die folgenden Gleichungen.

Da eine Amplitude von –3 dB, also ![]() 1/2 der Energie, entspricht, wird dieses Berechnungsverfahren als Halbbandbreitenverfahren bezeichnet.
1/2 der Energie, entspricht, wird dieses Berechnungsverfahren als Halbbandbreitenverfahren bezeichnet.
Anmerkungen:
Das Dämpfungsverhältnis kann durch das Halbbandbreitenverfahren nur erhalten werden, wenn der Wert von ζ klein ist (höchstens 0,1 oder weniger). Mit anderen Worten, wenn die Frequenz/Amplituden-Charakteristik eine deutliche Einzelspitzencharakteristik zeigt, wie in Fig. 3, können das Dämpfungsverhältnis und der Dämpfungskoeffizient durch das Halbbandbreitenverfahren erhalten werden. (Siehe (Ergänzung) „Berechnungsableitung der Halbbandbreitenmethode“ .)
Das Dämpfungsverhältnis und das logarithmische Dekrement werden als Bewertungsindizes und Konstruktionsparameter für Schwingungseigenschaften von Maschinen und Strukturen verwendet. Der Verlustfaktor wird als Bewertungsindex für die Dämpfungsmaterialien verwendet. Der Q-Wert wird zur Bewertung der elektrischen und mechanischen Resonanzeigenschaften verwendet. Wenn der Dämpfungskoeffizient des Materials mit großem Verlustfaktor erhalten wird, wird das Dämpfungsratenverfahren, das aus der Dämpfung pro Sekunde erhalten wird, oder das Impedanzverfahren verwendet. Die Leistungsmessung von Dämpfungsmaterial wird im Folgenden näher erläutert.
3. Dämpfungswirkung
Bisher haben wir erklärt, wie man Dämpfungsgrad und Verlustfaktor unter der Annahme ermittelt, dass die Amplitude exponentiell abnimmt. Nun soll kurz erklärt werden, was Dämpfungsverhältnis physikalisch bei Schwingungen bedeutet.
3.1 Dämpfungswirkung bei freier Schwingung
Freie Schwingung ist eine Schwingung, auf die keine äußere Kraft einwirkt. Wenn keine äußere Kraft angewendet wird, bleibt es stehen. Wenn jedoch eine Anfangsverschiebung oder Anfangsgeschwindigkeit als Anfangsbedingung hinzugefügt wird, beginnt die Vibration. Am Beispiel des in Abb. 4 gezeigten Federmassenmodells ziehen Sie zuerst die Masse m des Blocks, addieren eine Verschiebung (Anfangsverschiebung) auf die Feder k und lassen sie plötzlich los, dann beginnt die Vibration. Das ist die freie Schwingung.

Abbildung 4: Freischwingungsmodell
Ist die Dämpfungskraft c null, setzt sich die freie Schwingung dauerhaft fort. Die Vibrationsfrequenz ω 0 wird in der folgenden Gleichung ausgedrückt.

ω 0 wird als Eigenfrequenz bezeichnet. Erfahrungsgemäß hält die freie Schwingung nicht unbegrenzt an. Die Dämpfungskraft c wirkt, die Amplitude nimmt allmählich ab, wie in Fig. 1 dargestellt, und hört schließlich auf. Das Verhalten unterscheidet sich abhängig davon, ob der Wert von c größer oder kleiner als c c in der folgenden Gleichung ist.



Abbildung 5: Antwort der freien Schwingung
Wenn ζ < 1, wird die Amplitude der gedämpften freien Schwingung in der folgenden Gleichung gezeigt.

x 0 : anfängliche Verschiebung
v 0 : Anfangsgeschwindigkeit
ω d wird als Eigenfrequenz des Vibrationssystems bezeichnet und in der folgenden Gleichung gezeigt.

ω d ist etwas kleiner als ω 0 . Tatsächlich liegt ω d nahe bei ω 0 , da der Wert von ζ im tatsächlichen Schwingungssystem klein ist. Wie aus Gleichung (14) ersichtlich, wird das Verhalten des gedämpften Schwingungssystems durch die Anfangsbedingungen und das Dämpfungsverhältnis ζ bestimmt . Wenn die Anfangsgeschwindigkeit 0 und die Anfangsverschiebung 1 ist, ist die Reaktion aufgrund des Unterschieds im Dämpfungsverhältnis ζ in Fig. 5 gezeigt. Es ist ersichtlich, dass das Verhalten in Abhängigkeit vom Dämpfungsverhältnis ζ stark variiert . Wenn ζ
≥ 1, kann sie nicht durch Gleichung (14), sondern durch eine andere Gleichung berechnet werden. Zum Vergleich sind diese Reaktionen in Abbildung 5 dargestellt. ζ = 1 wird als kritische Dämpfung bezeichnet, ζ > 1 als Überdämpfung, 1 > ζ > 0 als Unterdämpfung. In Fig. 5 wird zum leichteren Verständnis ζ = 1 (kritische Dämpfung) betont, aber dies gibt nur die Grenze an, ob es vibriert oder nicht, und es bedeutet nicht, dass kritische Dämpfung besonders wichtig ist. Die Antwort ist in Abb. 5 dargestellt, wenn ζ =0,707 (=![]() ), dies ist wichtig für stationäre Schwingungen. Obwohl es ein gewisses Überschwingen (Unterschwingen) gibt, ist dies ein Wert, der häufig verwendet wird, wenn die Reaktionszeit für das Steuersystem wichtig ist, da der Wert die Einschwingzeit minimiert (das ist die Reaktion, um innerhalb von 5 % des Zielwerts zu konvergieren).
), dies ist wichtig für stationäre Schwingungen. Obwohl es ein gewisses Überschwingen (Unterschwingen) gibt, ist dies ein Wert, der häufig verwendet wird, wenn die Reaktionszeit für das Steuersystem wichtig ist, da der Wert die Einschwingzeit minimiert (das ist die Reaktion, um innerhalb von 5 % des Zielwerts zu konvergieren).
3.2 Dämpfungswirkung bei stationärer Schwingung
Als nächstes erläutern wir den Fall, in dem eine kontinuierliche Kraft von außen auf das Freischwingungssystem ausgeübt wird. Wenn eine äußere Kraft ausgeübt wird, spricht man von erzwungener Vibration. Wenn die externe Kraft eine Sinuswelle ist und ausreichend Zeit verstrichen ist (stationärer Zustand), spricht man von stationärer Schwingung. Während der Zustand vor dem stationären Zustand als Übergangszustand bezeichnet wird, wird er später erklärt. Wie in Abbildung 6 gezeigt, untersuchen wir ein Modell, in dem eine anregende Kraft 
auf ein Schwingungssystem mit einem einzigen Freiheitsgrad ausgeübt wird. Symbole und Gleichungen werden wie folgt dargestellt:

Abbildung 6: Modell der anregenden erzwungenen Schwingung

Da die anregende Kraft eine sich wiederholende Kraft mit der Frequenz ω ist, hat auch die durch die anregende Kraft angetriebene Schwingung im stationären Zustand dieselbe Frequenz. Amplitude und Phase sind jedoch unterschiedlich. Somit erhalten wir sie wie folgt. Die Bewegungsgleichung des in Fig. 6 gezeigten Systems wird durch die folgende Gleichung ausgedrückt. Durch Lösen dieser Gleichung können Amplitude und Phase der Schwingung im stationären Zustand erhalten werden.

Gleichung der stationären Schwingung ist;

Amplitude x a und Phase φ werden wie folgt gezeigt
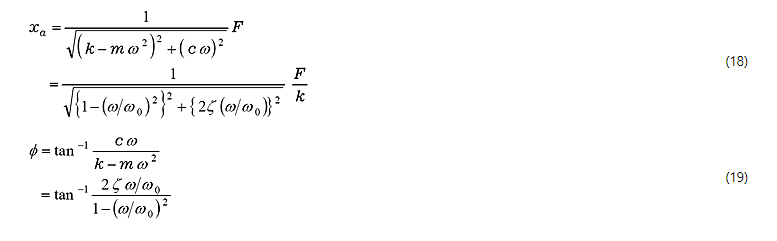
In Gleichung (18) ist F/k die statische Verschiebung, wenn die statische Kraft F aufgebracht wird. Um F / k zu ersetzenmit x s ist Gleichung (18).
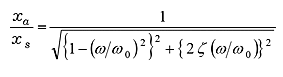
heißt Amplitudenvergrößerung. Fig. 7 ist im Logarithmus gezeigt, wobei ω / ω 0 auf der horizontalen Achse und die Amplitudenvergrößerung auf der vertikalen Achse aufgetragen sind. Diese Figur zeigt, dass Schwingungen im stationären Zustand um ω 0 in Resonanz sind und die Amplitudenvergrößerung stark durch die Dämpfungsrate ζ beeinflusst wird.

Abbildung 7: Abb.7 Amplitudenvergrößerung
Die Charakteristik der Amplitudenvergrößerung ist hier zusammengefasst:
Wenn ![]() , hat es einen Resonanzpunkt bei
, hat es einen Resonanzpunkt bei ![]() als Resonanzfrequenz. Je größer ζ ist, desto kleiner ist die Resonanzfrequenz ω r . Wenn ζ klein ist (etwa ζ <0,05), schwingt es mit der natürlichen Schwingung mit, aber nicht mit . Die Amplitudenvergrößerung ist bei der Resonanzfrequenz maximal.
als Resonanzfrequenz. Je größer ζ ist, desto kleiner ist die Resonanzfrequenz ω r . Wenn ζ klein ist (etwa ζ <0,05), schwingt es mit der natürlichen Schwingung mit, aber nicht mit . Die Amplitudenvergrößerung ist bei der Resonanzfrequenz maximal. ![]()

Wenn ζ klein ist;

Es ist gleich Q. Das bedeutet, dass es oft als Q behandelt wird, wenn die Resonanz scharf ist. Die Amplitudenvergrößerung liegt nahe bei 1 bei einer Frequenz, die niedriger als der Resonanzpunkt ist. Die Amplitudenvergrößerung liegt nahe bei ![]() , d. h. einer Steigung von –40 dB/Dekade. Die Phasendifferenz zwischen anregender Kraft und stationärer Schwingung ist in Gleichung (19) gezeigt. Dies ist in Abb. 8 grafisch dargestellt.
, d. h. einer Steigung von –40 dB/Dekade. Die Phasendifferenz zwischen anregender Kraft und stationärer Schwingung ist in Gleichung (19) gezeigt. Dies ist in Abb. 8 grafisch dargestellt.

Abbildung 8: Phasenverzögerung der Schwingung im stationären Zustand
Wenn die Frequenz der Anregungskraft niedriger als ω 0 ist (unterer Frequenzbereich), liegt die Phasenverzögerung der Vibration im stationären Zustand nahe bei 0 Grad, das heißt, die Vibration im stationären Zustand schwingt mit einer gegenüber der Anregungskraft geringfügig verzögerten Phase. In einem Frequenzbereich höher als ω 0 liegt die Phasenverzögerung der Schwingung im stationären Zustand nahe bei 180 Grad, das heißt, die Schwingung im stationären Zustand schwingt in entgegengesetzter Phase zur Anregungskraft. ζ ist klein, die Phase wird drastisch geändert, während ζ größer ist, ist die Änderung sanft.
3.3 Dämpfungswirkung bei transienter Vibration
Im vorigen Artikel haben wir über stationäre Vibrationen erklärt, wenn genug Zeit vergangen ist, seit die externe Kraft aufgebracht wurde. Jetzt erklären wir den Übergangszustand, der der Zustand ist, in dem die äußere Kraft angewendet wird, bis der stationäre Zustand gelesen wird. Betrachtet man das Schwingungssystem in Fig. 6, ist die Bewegungsgleichung Gleichung (24), jedoch nehmen wir zum leichteren Verständnis an, dass eine äußere Kraft vorhanden ist ![]()
und die Anfangsbedingung vollständig stationär ist, d. h. die Anfangsverschiebung und Anfangsgeschwindigkeit sind null.

Da dieses System linear ist, gilt das Prinzip der Überlagerung. Die Lösung ergibt sich aus der Summe der Schwingungsanteile durch äußere Krafteinwirkung und des freien Schwingungsanteils.
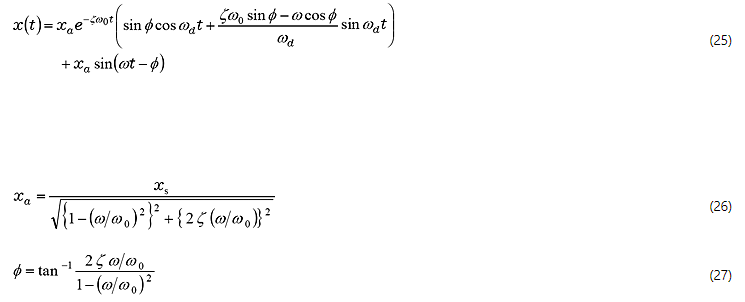
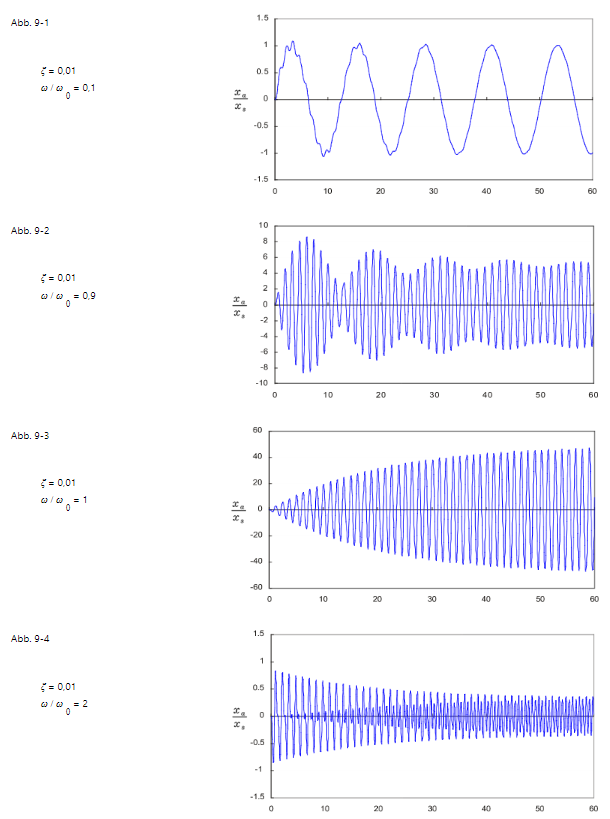
Der erste Term von Gleichung (25) ist eine freie Vibrationskomponente, sie wird allmählich gedämpft, und schließlich bleibt nur die stationäre Vibrationskomponente des zweiten Terms übrig. Dies ist in den Abbildungen 9-1 bis 9-4 dargestellt. Hier ist ζ = 0,01, die Änderung des Einschwingverhaltens wird angezeigt, wenn ω / ω 0 auf 0, 1, 0, 9, 1, 0 und 2, 0 geändert wird.
Wenn ω / ω 0 klein ist, wird die freie Schwingung mit der Zeit allmählich gedämpft und wird zu einer stationären Schwingung als einer freien Schwingung, die einer stationären Schwingung überlagert ist.
Wenn ω / ω 0 nahe bei 1 liegt, das heißt, wenn sich die Anregungsfrequenz der Eigenschwingungsfrequenz nähert, nimmt die Amplitude zu und die Schwebung wird erzeugt.
Wenn ω / ω 0 = 1, das heißt die Anregungsfrequenz gleich der Eigenfrequenz ist, nimmt die Amplitude proportional zur Zeit zu und wird zum Resonanzzustand.
Wenn ω / ω 0 >1, nimmt die Amplitude ab, wird aber zu einer komplizierten Wellenform.
Hier ist ζ = 0,01 auf einen kleinen Wert eingestellt, um den Übergangszustand leicht verständlich zu machen. Wenn jedoch ζ groß ist, konvergiert die freie Schwingung schnell und die Amplitude der stationären Schwingung nimmt ebenfalls ab. Diese Amplitude ist wie in Fig. 7 gezeigt. Wenn andererseits ζ klein ist, konvergiert der Übergangszustand nicht bald, und der instabile Zustand wird für eine lange Zeit andauern. Insbesondere bei Frequenzen in der Nähe von ω / ω 0 = 1 nimmt die Amplitude selbst bei einer anfänglich kleinen Schwingung allmählich zu und wird zu einer sehr großen Schwingung. (Hinweis: Die Skalierung der vertikalen Achse ist in Abb. 9.1 bis 9.4 unterschiedlich.)
Abbildungen 9.1 | 9.2 | 9.3 | 9.4
4. Zusammenfassung des relationalen Ausdrucks
Die Wechselbeziehungen von Koeffizienten, die Dämpfungseigenschaften darstellen, sind unten gezeigt.

5. Fazit
Für die mechanische Konstruktion ist es wichtig, die Vibrationen innerhalb des zulässigen Bereichs zu halten, da Vibrationen ein unvermeidbares Phänomen während des Maschinenbetriebs sind. Achten Sie besonders auf Resonanz, da diese selbst bei geringer äußerer Kraft große Vibrationen verursachen kann. Es ist ideal, nicht gleichzeitig eine natürliche Resonanzfrequenz (Eigenfrequenz) und eine erzwungene Vibrationsfrequenz zu haben. Realistischerweise gibt es jedoch eine Eigenfrequenz innerhalb des Betriebsbereichs, und es ist ein schwieriges Problem für Ingenieure, dieses Phänomen zu lösen.
Wie in diesem Artikel erläutert, variiert das Resonanzverhalten stark mit der Dämpfung. Daher ist es vernünftig, bei der Konstruktion eine angemessene Dämpfung vorzusehen, um die Schwingung auf einem zulässigen Niveau zu halten. Das Hinzufügen von Dämpfungselementen wie Dämpfern wird häufig verwendet, um Vibrationen zu reduzieren, die von Maschinen oder Strukturen erzeugt werden. In diesem Fall sind Grundkenntnisse über Dämpfung erforderlich, die wir erklärt haben. Obwohl wir ein einfaches Modell erklären, das ein System mit 1 Freiheitsgrad hat und die externe Kraft eine Sinuswelle ist, haben die tatsächlichen Maschinen und Strukturen kompliziertere Systeme, die externe Kraft ist eine unregelmäßige Wellenform. Es ist nicht einfach, Vibrationen zu analysieren, da die Dämpfungsrate mit der Amplitude oder dem Zustand variiert. Die grundlegende Theorie der mechanischen Vibration ist ein Systemmodell mit 1 Freiheitsgrad, und der größte Teil des Vibrationsverhaltens wird durch das Wissen erklärt, das wir in diesem Artikel erläutert haben.
Wir haben kurz die Bedeutung von Koeffizienten erläutert, die die Dämpfungscharakteristik darstellen, hauptsächlich die Dämpfungsrate. Es wäre sehr zu schätzen, dass dieser Artikel für die Person nützlich ist, die kein Experte für Vibrationen ist, wenn sie Gegenmaßnahmen ergreifen.
5.1 ⟨Ergänzung⟩ Berechnungsmethode der Halbbandbreitenmethode
Die Gleichung der maximalen Amplitude (22) wird erhalten, indem die Gleichung der Resonanzfrequenz in die Gleichung der Amplitudenvergrößerung (21) eingesetzt wird.

Einsetzen der Resonanzfrequenzgleichung
![]()
in ![]()
Gleichung (21)
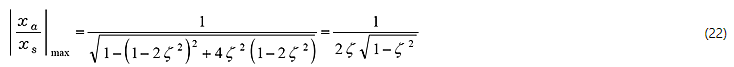
Erhalt der Frequenz mit der maximalen Amplitude
![]()
aus Gleichung (21) und (22).
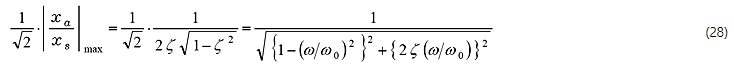
Neuordnung:
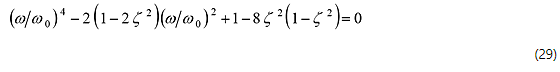
Dies lösen;
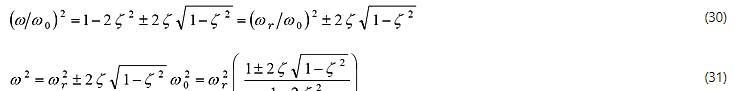
Wenn ζ ≪ 1, ζ 2 ≒ 0. Dann;
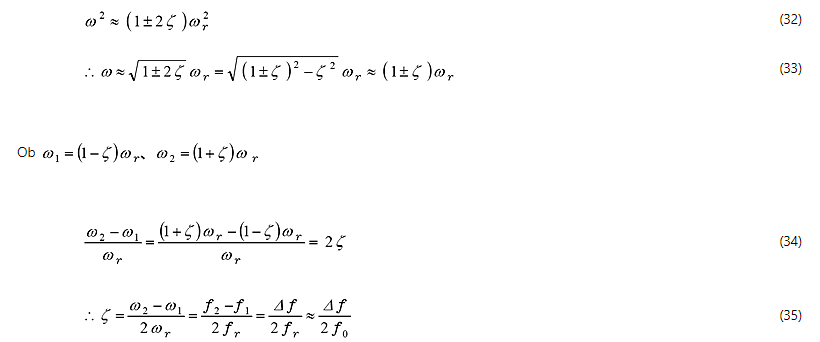
Wie oben gezeigt, wird eine genaue Berechnung durchgeführt, wenn ζ 0,05 oder weniger oder bis zu den höchsten 0,1 oder weniger beträgt, da die Gleichung, die die Dämpfungsrate aus dem Halbbandbreitenverfahren erhält, nahe an der Gleichung liegt, wenn ζ ≪ 1 ist.
5.2 (Referenz) Dämpfungsgrad für Struktur und Maschinen
Die tatsächliche Dämpfungsrate für Struktur und Maschinen sind wie folgt:
| Gebäude aus Stahlrahmen | 0,003 bis 0,04 |
| Mittelniedriges Gebäude (10 Stockwerke oder weniger) | 0,005 bis 0,12 |
| Mehrstöckiges Gebäude | 0,02 bis 0,1 |
| Turm aus Stahl | 0,002 bis 0,03 |
| Turm aus Beton | 0,01 bis 0,02 |
| Autobahnbrücke | 0,02 bis 0,05 |
| Hängebrücke | 0,002 bis 0,08 |
| Aufhängung für große Automobile | 0,1 bis 0,3 |
| Aufhängung für Kleinwagen | 0,2 bis 0,5 |
| Aufhängung für Motorrad | 0,35 bis 0,45 |
(Referenzmaterialien)
„Vibrationssteuerung“ geschrieben von Kohei Suzuki, Ohmsha (geschrieben auf Japanisch)
„Compendium of Automotive engineering 11“, Sankaido (geschrieben auf Japanisch)

