Informationen
FFT-Analysator
Inhaltsverzeichnis
1. Was ist FFT?
1.1 FFT-Analysator
1.2 Warum ist FFT notwendig?
2. Darstellung von Wellenformen (Sinus- und Cosinuswelle)
2.1. Amplitude, Phase, Frequenz
2.2. Ort der Wellen
2.3 Zeitdifferenz und Phase
2.4 Elektrischer Winkel und mechanischer Winkel
2.5 Ordnung und Harmonische von 2-5 U/min
2.6 Darstellung von Wellenformen (Summe der Wellenform (Zusammensetzung))
2.7 Darstellung von Wellenformen (Produkt von Wellenformen)
3. Fourier-Reihen und Fourier-Transformationen
3.1 Fourier-Reihe
3.2 Darstellung der Fourier-Reihe durch komplexe Exponentialfunktion
3.3 Fourier-Transformation
3.4 Diskrete Fourier-Transformation
3.5 Abtasttheorem
1. Was ist FFT?
Die kontinuierliche Fourier-Transformation wurde von einem französischen Mathematiker und Wissenschaftler, Fourier, als natürliche Weiterentwicklung seiner Fourier-Reihentheorie entdeckt. Die Fourier-Reihentheorie besagt, dass jede Wellenform, wie kompliziert sie auch sein mag, als eine Reihe von zwei oder mehr einfachen Sinuswellen und Kosinuswellen ausgedrückt werden kann, wenn die Wellenform periodisch ist, d. h. aus denselben wiederholten Wellenformen besteht. Der mathematische Ausdruck dieser Theorie heißt Fourier-Reihe. Die Fourier-Transformation beinhaltet die Erweiterung der Fourier-Reihe von -∞ nach +∞ als kontinuierliche Funktion. Es ist nicht immer klar, inwieweit ein Signal tatsächlich gemessen und als periodisch bestimmt werden kann, insbesondere wenn die Wellenform bis unendlich gemessen wird, da sie in der Praxis immer schwächer wird. Somit wird im Allgemeinen nur ein Teil der beobachteten Wellenform ausgeschnitten und an diesem Periodenteil der Wellenform eine Fourier-Transformation durchgeführt, wobei angenommen wird, dass sich das Wellenformmuster unendlich wiederholt. Ursprünglich erforderte diese Fourier-Transformationsberechnung eine enorme Anzahl von Multiplikationsberechnungen. JW Cooley und JW Tukey schlugen jedoch ein Berechnungsverfahren vor, das die Anzahl der einzelnen Berechnungen reduziert, indem die Anzahl der Messpunkte gleich 2 n genommen wird. Wenn die Anzahl der Messpunkte mit 1024 angenommen wird, wird die Anzahl der Multiplikationen, d. h. 1024 x 1024 = 1048576, auf 10240 reduziert. Dieses Verfahren wurde als schnelle Fourier-Transformation bezeichnet und wird häufig mit seinem Akronym FFT bezeichnet.
1.1 FFT-Analysator
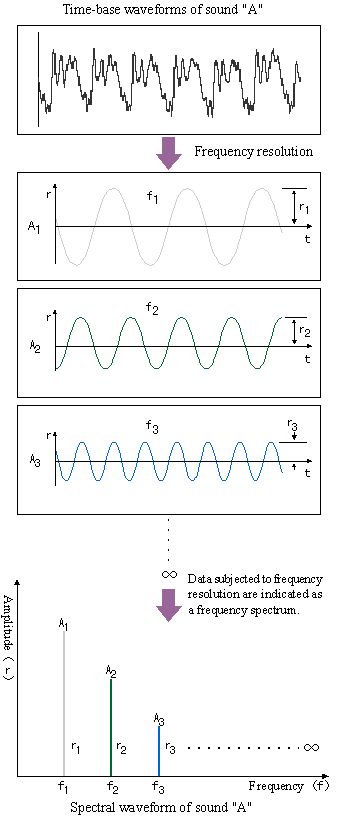
Abbildung 1.1
Eine FFT-Berechnung zeigt anschaulich, wie die Koeffizienten einer Fourier-Reihe (Fourier-Koeffizienten) bestimmt werden. Ein FFT-Analysator speichert eine Eingangssignalwellenform als Daten, indem er sie digital (diskret) abtastet, bestimmt die Fourier-Koeffizienten in kurzer Zeit unter Verwendung von FFT und zeigt die Ergebnisse dieser Analyse an. Da die FFT-Analyse im Wesentlichen ein Signal in einfache Frequenzen zerlegt, indem die Amplitude gegen Frequenzbereiche als Spektrum aufgetragen wird, wird der FFT-Analysator auch als Frequenzanalysator oder Spektrumanalysator bezeichnet.
Beispielsweise erzeugt eine Analyse des gesprochenen Buchstabens „A“ mit einem FFT-Analysator die spektralen Wellenformen in Abbildung 1.1, die die Frequenz f der Schallwellenform entlang der X-Achse und die Amplitude r entlang der Y-Achse angeben. Diese spektralen Wellenformen zeigen an, dass der Schall von "A" aus Wellen besteht, deren Frequenzen f 1 , f 2 , f 3 ..., f n sind und deren Amplituden r 1 , r 2 , r 3 , ... sind. ....,r n . Anders ausgedrückt stellt dieser Graph eine Kombination von Wellen dar, deren Frequenzen f 1 , f 2 , f 3 ..., f n sind und deren Amplituden r 1 , r 2 , r 3 , ... sind. .,r n, die sich zusammensetzen, um die Klangwellenform von "A" zu bilden.
Abbildung 1.2 zeigt die tatsächlich gemessenen Zeitbasis-Wellenformen und ihr Klangspektrum "A". Der untere Graph zeigt die Zeitbasiswellenformen und der obere Graph zeigt die spektralen Wellenformen. Frequenzen, die als Spitzen im linken Teil der spektralen Wellenformen erscheinen, entsprechen f 1 , f 2 , f 3 , ..., f n .
Betrachten wir nun FFT für konkretere Beispiele.
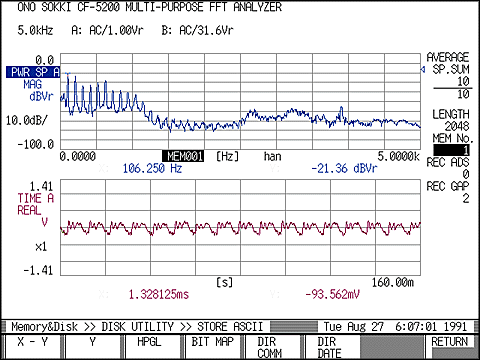
Abbildung 1.2
1.2 Warum ist FFT notwendig?
Lassen Sie uns die Wellenformen der Vibration beobachten, die von einer realen Maschine erzeugt werden. Installieren Sie einen Beschleunigungsaufnehmer an einem Lager, wie in Abbildung 1.3 gezeigt, und beobachten Sie die vom Beschleunigungsaufnehmer erhaltenen Vibrationswellenformen. Zusammengesetzte Wellenformen können entlang der Zeitachse wie im Fall des gesprochenen "A" beobachtet werden.
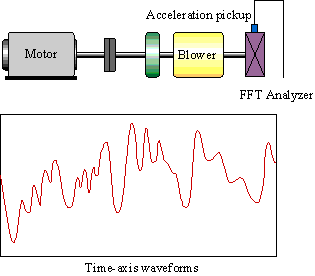
Abbildung 1.3
Warum einen FFT-Analysator für die Frequenzanalyse verwenden d.h. die Frequenz von Wellenformen beobachten?
Die in Abbildung 1.3 gezeigte zusammengesetzte Wellenform kann als kombinierte Wellenform angesehen werden, die aus den Vibrationen an jeder Position der Maschine erhalten wird (siehe Abbildung 1.4).
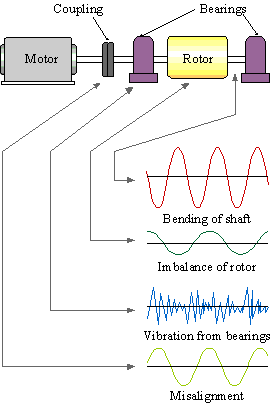
Abbildung 1.4
Abbildung 1.5 ist ein konzeptionelles Diagramm, das die Beziehung zwischen dem Ergebnis der Analyse der zusammengesetzten Vibrationswellenformen dieser rotierenden Maschine zeigt, die unter Verwendung eines FFT-Analysators erhalten wurden, und den Positionen der Vibrationsquellen.
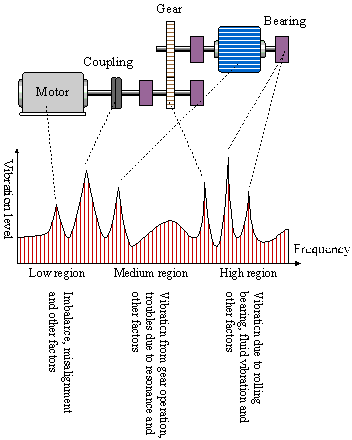
Abbildung 1.5
Die Frequenzen, die der von jeder Position erzeugten Vibration entsprechen, werden durch die Konstruktion der Maschine bestimmt. In der Vergangenheit wurde bei der Wartung und Kontrolle von Anlagen sowie bei der Diagnose von Anomalien ein Maß für die Gesamtschwingung, also ein Gesamtwert, mit einem Schwingungsmessgerät gemessen. Da ein Gesamtwert jedoch nur unterscheidet, ob die Vibration stark oder schwach ist, konnte der tatsächliche Ort der Anomalie nicht identifiziert werden.
Durch häufiges Beobachten einer Wellenform mit einem Oszilloskop (im Zeitbereich) konnten wir sehen, wie sich die Wellenform im Laufe der Zeit ändert (Wellenformen auf der Zeitachse), aber es war schwierig, die Ursache dieser Änderung zu bestimmen. Es war nicht möglich, die Ursache der Anomalie und der anormalen Positionen abzuschätzen, bis die mit FFT erhaltenen Frequenzanalysedaten es uns ermöglichten, den Grad der Änderung zu untersuchen, der bei welchem Frequenzniveau auftrat, und die von einer bestimmten Position erzeugten Frequenzen. In den frühen Stadien des Ausfalls oder bei leichten Anomalien zeigt der Gesamtwert der Zeitachsenwellenformen nur sehr geringe Änderungen, wodurch der Ausfall/die Anomalie sehr schwer zu erkennen ist. Die Frequenzanalyse (Beobachtung der Wellenform im Frequenzbereich) ermöglicht die Erkennung selbst geringfügiger Anomalien.
Neben der Anlagensteuerung und der Fehlerdiagnose mittels Schwingungsanalysen wird die Frequenzanalyse heute in verschiedenen weiteren Bereichen eingesetzt, beispielsweise zur Beurteilung der Laufruhe und zur Geräuschanalyse von Bürogeräten und elektrischen Haushaltsgeräten, um die Ursache von Geräuschen und mögliche Gegenmaßnahmen zu untersuchen.
2. Darstellung von Wellenformen (Sinus- und Cosinuswelle)
Um die Bedeutung der von einem FFT-Analysator gelieferten Daten zu verstehen, ist es notwendig, das Konzept der Fourier-Reihe zu verstehen – die Grundlagen der FFT und ihren mathematischen Hintergrund. Dieses Kapitel erklärt die Darstellung von Schall als Wellenformen, die zum Verständnis der Fourier-Reihe und der Eigenschaften der Sinus- und Kosinuswelle erforderlich ist.
2.1 Amplitude, Phase, Frequenz
Amplitude
Die Amplitude zeigt die Größe der Wellenform. Nehmen wir Schall als Beispiel: Ein lauter Schall hat eine große Amplitude. Mit verschiedenen Sensoren werden unterschiedliche physikalische Phänomene erfasst. Vibration wird mit einem Vibrationssensor gemessen, Schall mit einem Schallpegelmesser, Kraft mit einer Wägezelle und Druck mit einem Drucksensor. Das Signal wird als Spannungsamplitudenwert proportional zum Wert der physikalischen Größe ausgegeben. Die Zeitachsen-Wellenform (Abbildung 2.1), die in einem FFT-Analysator angezeigt oder mit einem Oszilloskop oder Stiftschreiber gemessen wird, ist die Beobachtung des Spannungsausgangs über die Zeit.
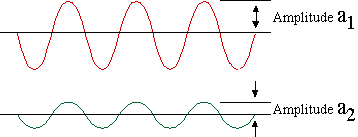
Abbildung 2.1
Frequenz
Die Frequenz stellt die Anzahl der in einer Sekunde wiederholten Wellenperioden dar und wird in Einheiten von Hz definiert. Es gilt die folgende Beziehung, wobei die Frequenz durch f und die Periode durch T dargestellt wird.
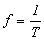
Gleichung 2.1
In Bezug auf Ton wird anerkannt, dass Wellenformen hoher Frequenz hohen Tönen und Wellenformen niedriger Frequenz tiefen Tönen entsprechen (Abbildung 2.2).
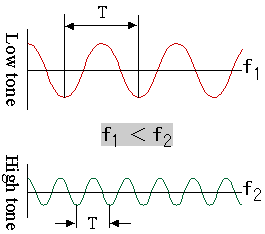
Abbildung 2.2
Phase
Eine Periode einer Welle wird als elektrischer Winkel von 360º oder 2p Radiant dargestellt. „Grad“ wird zu Erklärungszwecken verwendet, aber in mathematischen Ausdrücken wird „Bogenmaß“ im Allgemeinen verwendet und einfach als „rad“ ausgedrückt. Die Position eines Peaks kann sich, wenn er zu einem bestimmten Zeitpunkt gemessen wird, sogar zwischen Wellen gleicher Frequenz unterscheiden. Der Unterschied in der Spitzenposition einer gegebenen Wellenform von der Referenzwellenform wird üblicherweise als eine Größe ausgedrückt, die als "Phasendifferenz" bezeichnet wird. Die Phase wird als "negativ" angesehen, wenn die bestimmte Spitze hinter der entsprechenden Spitze in der Referenzwellenform zurückbleibt, oder als "positiv", wenn sie nach der entsprechenden Spitze kommt (Abbildung 2.3).
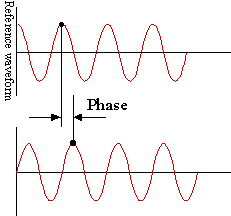
Abbbildung 2.3
2.2 Ort der Wellen
Betrachten wir die Bewegung eines Balls, wenn er an einer Schnur befestigt ist und sich um den Ursprung der Schnur dreht. Der Ort des Balls ist in Abbildung 2.4 dargestellt.
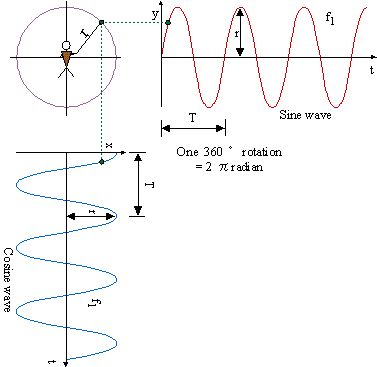
Abbildung 2.4
In Abbildung 2.4 stellt die Wellenform, die durch den Ort des Schattens des auf die Y-Achse projizierten Balls erhalten wird, eine Sinuswelle dar, und die Wellenform, die durch den Ort des Schattens des auf die X-Achse projizierten Balls erhalten wird, repräsentiert einen Kosinus Welle. Die Länge der Saite (r) entspricht der Amplitude und die Zeit für eine volle Umdrehung der Kugel der Periode (T). Wenn der Winkel einer Drehung des Balls in Radiant ausgedrückt wird, ist 360° = 2p Radiant, und der Winkel, den der Ball in der Zeit t dreht, kann aus Gleichung 2.2 berechnet werden,

Gleichung 2.2
wobei die Frequenz f die Anzahl der Umdrehungen angibt, die der Ball in einer Sekunde macht, und durch die Gleichung 2.3 gegeben ist,

Gleichung 2.3
Dann werden die Orte jedes Schattens nach der Zeit t in den folgenden mathematischen Gleichungen ausgedrückt.

Gleichung 2.4
Diese beiden Gleichungen zeigen die Position des Balls nach der Zeit t als XY-Koordinaten (x,y).
Wenn wir nun annehmen, dass die Kugel an der Position ist, die durch den Winkel f erreicht wird, wie in Abbildung 2.5 gezeigt, dann erhalten die Gleichungen 2.4 Folgendes:
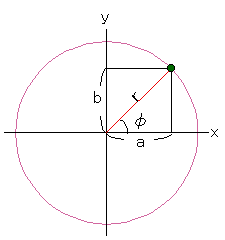
Abbildung 2.5
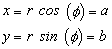
Gleichung 2.5
Da a, b und r als die drei Seiten eines rechtwinkligen Dreiecks angesehen werden können, gilt auch die folgende Gleichung.

Wie oben zu sehen ist, wird die Ballposition spezifisch bestimmt, indem entweder a und b in den Gleichungen 2.5 oder r und f verwendet werden, unabhängig von der Anzahl der Umdrehungen des Balls.
Es gibt viele physikalische Phänomene, die eine Periodizität aufweisen und daher als Wellenphänomene klassifiziert werden. Die Sinus- und Kosinusfunktion werden zusammen mit der Tangensfunktion als trigonometrische Funktionen in den mathematischen Ausdrücken verwendet, die solche Phänomene erklären.
Nehmen wir an, dass die Position des Winkels f der Startpunkt ist (in diesem Fall repräsentiert f die Anfangsphase). Dann kann Gleichung 2.4 wie unten gezeigt ausgedrückt werden.

Gleichung 2.7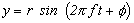
Gleichung 2.8
Der Ausdruck, der den Ort der Ballbewegung darstellt, kann entweder Gleichung 2.7 oder Gleichung 2.8 sein. Gleichung 2.7, die auf Kosinus basierende Funktion, wird jedoch im Allgemeinen verwendet, da eine Sinuswelle als eine Kosinuswelle mit einer Phasenverzögerung von p/2 angesehen wird und Formeln, die physikalische Phänomene darstellen, oft unter Verwendung von auf Kosinus basierenden Funktionen ausgedrückt werden Leichtigkeit beim Lösen.
Im nächsten Abschnitt werden die verwandten Wellenformausdrücke und die wichtigen allgemeinen Begriffe der FFT-Wellenformanalyse erläutert.
2.3 Zeitdifferenz und Phase
Schreit eine Person auf einen Berg zu, ertönt kurze Zeit später ein Echo. Betrachten wir, wie die Zeitdifferenz zwischen der Zeit des Schreis und der Zeit der Echorückkehr als Phasendifferenz ausgedrückt wird.
Wenn die Periode der Wellenform durch T dargestellt wird, die Frequenz durch f, die Zeitdifferenz durch t und die Phase durch f, dann:

Gleichung 2.9
Wenn beispielsweise in der vorherigen Wellenform des Tons „A“ die Frequenz von „A“ 106 Hz und die Zeitdifferenz zum Echorücklauf t = 0,001 Sekunden betrug, dann wird die Phase mit einer Verzögerung von ungefähr 0,21 berechnet p=38,1º. Wenn die Zeitdifferenz dieselbe ist, t = 0,001 Sekunden und die Frequenz von "A 2 " mit 212 Hz angenommen wird, dann tritt eine Phasenverzögerung von 76,3º auf. Dies zeigt, dass bei unterschiedlicher Periode T (Frequenz) auch die Phase unterschiedlich ist, selbst wenn die Zeitdifferenz gleich ist.
2.4 Elektrischer Winkel und mechanischer Winkel
Neben Amplitude, Frequenz und Phase ist es auch wichtig, den Unterschied zwischen dem elektrischen Winkel zu verstehen. Angenommen, ein elektromagnetischer Detektor ist für ein Zahnrad mit 60 Zähnen vorbereitet und das Zahnrad dreht sich mit 600 U/min. Wenn sich das Zahnrad eine volle Umdrehung dreht, wird ein Sinuswellensignal mit 60 Zyklen vom elektromagnetischen Detektor ausgegeben. Hier wird die Phase, die ausgedrückt wird, indem eine Periode der Signalsinuswelle als 2p rad (360º) genommen wird, ein "elektrischer Winkel" genannt, und die Phase, die ausgedrückt wird, indem eine Drehung des Zahnrads als 2p rad genommen wird, wird als "mechanischer Winkel" bezeichnet.
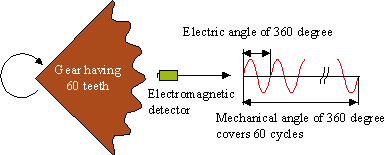
Abbildung 2.6
Wie in Abbildung 2.6 gezeigt,
die Frequenz der Signalsinuswelle, f = 600 U/min./60 s × 60 Zahnradzähne = 600 (Hz), und
die Rotationsfrequenz des Zahnrads, f 0 = 600 U/min./60 s = 10 (Hz).
Obwohl eine Periode der Signalsinuswelle und die des Zahnrads beide einen Winkel von 2prad haben, unterscheiden sich ihre Zeiten wie unten gezeigt:
Periode des Detektorsignals = Periode des elektrischen Winkelausdrucks = 2p = 1/600 Sekunde
Periode einer Zahnradumdrehung = Periode des mechanischen Winkelausdrucks = 2p = 1/10 Sekunde
Der elektrische Winkel basiert auf einer Periode elektrischer Signale, während der mechanische Winkel auf einer Periode einer Umdrehung eines Körpers basiert. Wenn die Phänomene rotierender Körper analysiert werden, müssen die Daten der Frequenzanalyse im Hinblick auf die Beziehung zwischen den elektrischen und mechanischen Winkeln betrachtet werden.
Ein FFT-Analysator verwendet elektrische Winkel.
2.5 Ordnung und Harmonische von 2-5 U/min
Die Drehzahlordnung wird häufig verwendet, um Phänomene im Zusammenhang mit Umdrehungen zu analysieren. Wenn die oben beschriebene Zahnraddrehung als Referenzfrequenz betrachtet wird, hat das Sinussignal eine Frequenz, die das 60-fache der Referenzfrequenz des Zahnrads ist. Dies wird als "sechzigste Harmonische" bezeichnet. Bei Rotationsmaschinen wird unter anderem mit dem Begriff „Rotation“ die Rotationsfrequenz (Umdrehungen pro Sekunde) des Zahnrads bezeichnet. Beispielsweise wird eine Drehung bei einer Frequenz von 10 Hz als Drehung 1. Ordnung bezeichnet, und eine Drehung basierend auf einem 600-Hz-Sinuswellensignal wird als Drehung 60. Ordnung bezeichnet.
Der Begriff Harmonische bezieht sich auf die Frequenzen von ganzzahligen Vielfachen der Grundfrequenz. Wenn beispielsweise die Frequenz der Grundwelle „A 1" des Tons "A" 106 Hz beträgt, dann beträgt die Frequenz seiner zweiten Harmonischen "A 2 " 212 Hz. Heutzutage wird die harmonische Verzerrungsanalyse an der Frequenz von Stromversorgungen durchgeführt. Dies beinhaltet die Analyse der ganzzahligen Vielfachen von harmonischen Komponenten oder die Amplituden und Phasen dieser Frequenzen, wenn die Netzgrundfrequenz beispielsweise 50 oder 60 Hz beträgt.
2.6 Darstellung von Wellenformen (Summe der Wellenform (Zusammensetzung))
Betrachten Sie die Summe der unten gezeigten Wellen (Zusammensetzung der Wellen).

Gleichungen 2.10
Die zusammengesetzten Wellenformen sind wie in (3) und (4) von Abbildung 2.7 gezeigt , jede hat die gleiche Frequenz, aber unterschiedliche Amplitude und Phase.
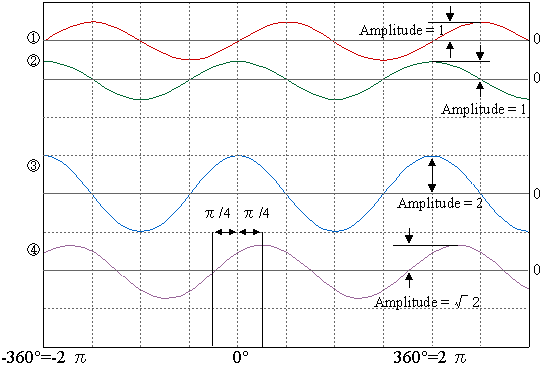
Abbildung 2.7
Betrachten wir zuerst x 2 . Die Gleichung von x 2 kann wie unten gezeigt unter Verwendung der trigonometrischen Formel umgeschrieben werden.

Gleichung 2.11
Das bedeutet, wenn eine Kosinuswelle und eine Sinuswelle mit der gleichen Frequenz und Phase zusammengesetzt werden, dann ist die resultierende Welle gleich einer Kosinuswelle mit der doppelten Wurzel der ursprünglichen Amplitude und einer Phasenverzögerung von p/4. Dies kann auch wie unten gezeigt erweitert werden.

Gleichung 2.12
Wenn der "a"-Koeffizient der Kosinuswelle auf der Kosinusachse und der "b"-Koeffizient der Sinuswelle auf der Sinusachse aufgetragen wird, erhält man Abbildung 2.8. Da diese Abbildung mit der vorherigen Abbildung 2.5 identisch ist, können die Gleichungen 2.6 wie folgt gelöst werden.
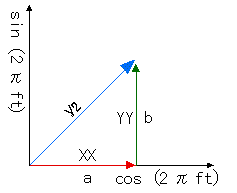
Abbildung 2.8
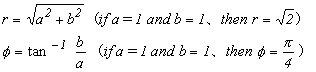
Gleichung 2.13
Das heißt, die Gleichungen 2.14 gelten.

Gleichungen 2.14
Wie oben zu sehen ist, kann eine Wellenform mit einer einzigen Frequenz (im Folgenden als einfache Wellenform bezeichnet) als eine Gleichung mit derselben Frequenz und denselben Koeffizienten von a und b ausgedrückt werden, wie unten gezeigt.
Wenn somit die Koeffizienten a und b gegeben sind, können der zusammengesetzte Amplitudenwert r und die Phasendifferenz bestimmt werden.
Wenn zum Beispiel die Koeffizienten der Gleichung der zusammengesetzten Wellenform x 1 = a cos (2 π f t) + b sin (2 π f t) a = 2 und b = 0 sind, dann ist der Wert der zusammengesetzten Amplitude r = 2 und die Phasendifferenz f = 0.
Die Komponenten „A ? “, „A 2 “, „A 3 “, ... des Tons „A“, der frequenzanalysiert wurde, sind jeweils einfache Wellenformen, die in der Form ausgedrückt werden können a cos (2 π f t) + b sin (2 π f t). Bitte beachten Sie zu Ihrer Information, dass die Phasendifferenz f ist cos (2 π f t).
2.7 Darstellung von Wellenformen (Produkt von Wellenformen)
Nachdem wir nun erklärt haben, wie einfache Wellenformen durch den Ausdruck " a cos (2 π f t) + b sin (2 π f t)" dargestellt werden können, erklärt dieser Abschnitt, wie die Koeffizienten des Ausdrucks tatsächlich bestimmt werden.
Betrachten wir die folgenden Produkte von Wellenformen.
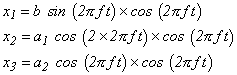
Gleichungen 2.15
Abbildung 2.9 zeigt Wellenformen der folgenden Ausdrücke, wenn a 1 = 2, a 2 = 3 und b = 2.
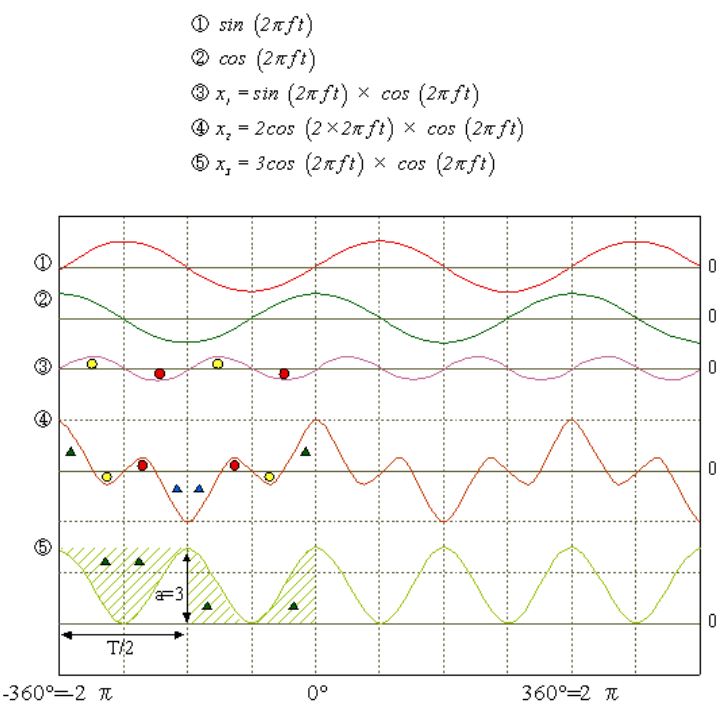
Abbildung 2.9
Wie in dieser Figur gezeigt, führt das Produkt periodischer Wellenformen zu einer Wellenform, die ebenfalls Periodizität aufweist. Betrachten wir den Bereich, der durch Integrieren der Wellenform von x 1 für eine Periode (von 0 bis 2p) erhalten wird. In der Wellenform x 1 sind die Fläche auf der positiven Seite ⬤ und die Fläche auf der negativen Seite ⬤ gleich, die Summe der Flächen ist also Null. Die Wellenform X 2 drückt das Produkt der Grundwellenform und der zweiten harmonischen Komponente aus. Der Bereich der Wellenform X 2 ist ebenfalls Null. Für die Wellenform von X 3 gibt es jedoch keine negative Seitenfläche und die Summe der Fläche.
Das ist,

Gleichung 2.16
Das bedeutet, dass die Amplitude a n aus einer beliebigen Wellenform der Form an cos (n x 2 π f t)," mit n=1,2,3,... bestimmt werden kann durch:
=> Multiplizieren der Wellenform mit cos (n x Multiplizieren der Wellenform mit cos (n x 2 π f t) um die Fläche für eine Periode zu bestimmen.
=> Teilen der erhaltenen Fläche durch T/2, und dann
=> Extrahieren der Originalkomponente cos (n x 2 π f t)
Wenn in ähnlicher Weise die obige willkürliche Wellenform mit multipliziert wird sin (n x 2 π f t), der Fläche der bestimmten Produktwellenform, und dann durch T/2 dividiert wird, dann kann die Amplitude b n bestimmt werden.
Dieser Bericht enthält eine konzeptionelle Erläuterung der FFT und der Grundlagen von Sinus- und Kosinuswellen, die zum Verständnis der Fourier-Transformation und der Fourier-Reihe erforderlich sind. In dieser Erklärung tauchen viele mathematische Ausdrücke auf. Hast du sie verstanden? Wir haben versucht, diesen mathematischen Ausdrücken eine Bedeutung zu geben, indem wir sie mit realen Zahlen dargestellt haben. Wenn Sie Fragen haben, können Sie diese gerne mit uns besprechen.
3. Fourier-Reihe und Fourier-Transformationen
Wie im vorherigen Bericht erwähnt, können Wellenformen, die sich periodisch im Zeitbereich ändern, mithilfe einer Fourier-Reihe ausgedrückt werden. In diesem Kapitel werden wir tatsächlich versuchen, diese periodischen Wellenformen auszudrücken, indem wir die Fourier-Reihe und die Fourier-Transformation verwenden.
3.1 Fourier-Reihen
Betrachten wir zunächst den Laut „A“ (ausgesprochen als „aah“), wie er in Abbildung 1-1, Kapitel 1 des vorherigen Berichts eingeführt wurde. Wie bereits erwähnt, kann der Laut „A“ in drei Elemente „A 1 “, „A 2 “ und „A 3 “ zerlegt werden . Darüber hinaus könnte die Wellenform von „A 1 “ als Kosinuswellen mit einer Phasendifferenz auf folgende Weise dargestellt werden:



Durch Neuanordnung von f1, f2, f3, ..., a1, a2, a3 ... bzw. b1, b2, b3, ... als fn, an, bn, (n = 1, 2, 3, ...) hier haben wir:

Gleichung 3.1
Wenn wir Gleichung 3.1 für den Ton „A“ mit der unten gezeigten Definitionsformel 3-2 für eine Fourier-Reihe vergleichen, stellen wir fest, dass die beiden auffallend ähnlich sind. Wenn die Grundfrequenz f 0 ist, sind die Komponenten f 1 , f 2 , f 3 , --- des Tons "A" f 1 = f 0 , f 2 = 2f 0 , f 3 = 3f 0 und entsprechen den 1. Harmonische, 2. Harmonische, 3. Harmonische, --- (Frequenzen in ganzzahligen Vielfachen von f 0 ). Da die beispielhafte Analyse des Tons „A“ in Abbildung 1-2 des vorherigen Berichts T = 160 ms (f 0 = 6,25 Hz) angenommen hat, entsprechen diese Harmonischen f 1= 106,25 Hz = 17f 0 (17. Harmonische), f 2 = 34f 0 und f 3 = 51f 0 in der Figur. Die Harmonischen, die nicht f 1 , f 2 , f 3 , --- entsprechen, können als andere Signalelemente betrachtet werden, die sich von "A" unterscheiden, wie beispielsweise Hintergrundrauschen.
Wie dem Obigen entnommen werden kann, ist das Konzept, das wir seit Abschnitt 2-2 des vorherigen Berichts diskutiert haben, nichts anderes als die Fourier-Reihe.
Werfen wir also einen Blick auf die Definitionsformel dieser Fourier-Reihe.
Wenn die Periode einer Wellenform, die sich periodisch im Zeitbereich ändert, durch T dargestellt wird, haben wir:
Grundfrequenz f 0 = 1/T
Grundkreisfrequenz ω0 = 2πf 0
Daher kann die Wellenform wie unten gezeigt in Form einer Fourier-Reihe ausgedrückt werden:

Gleichung 3.2
Unter Verwendung der Multiplikationen von Cosinus und Sinus aus Abschnitt 2.6 des vorherigen Berichts und der entsprechenden Flächenwerte können hier die Komponenten von Gleichung 3-2 gefunden werden:

Gleichung 3.3
a 0 ist eine DC-Komponente, und a n und b n sind die Amplituden von Cosinuswellen und Sinuswellen, deren Winkelfrequenz n ω0 ist . Diese letzten beiden werden Fourier-Koeffizienten genannt und gemeinsam als Fourier-Koeffizientenpaar bezeichnet.
Sehen wir uns nun die bisherige Erklärung an.
Gleichung 3.2 kann wie folgt interpretiert werden:
n ω0 t(n=1, 2, 3, ...) sind 1x, 2x, 3x, ... Harmonische der Grundkreisfrequenz ω0 , wobei die Wellenformen der Komponenten von n ω0 t ausgedrückt werden durch:
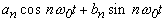
Die entsprechenden Fourier-Koeffizienten an und b n können durch Gleichung 3.3 gefunden werden. Darüber hinaus kann Gleichung 3-3 basierend auf der in Abbildung 3.1 unten gezeigten Beziehung zwischen a n und b n wie folgt dargestellt werden:

Abbildung 3.1
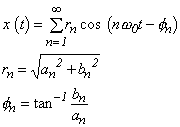
Gleichung 3.4
Wobei rn und n die Amplitude bzw. Phase der n-ten Harmonischen sind ϕ.
Ein FFT-Analysator speichert die berechneten Fourier-Koeffizienten a n und b n im Speicher und verwendet sie dann, um die Amplitude r n und die Phase ϕn der Frequenz f n zu berechnen . Basierend auf dieser Berechnung erzeugt der Analysator eine spektrale Anzeige, die die Beziehung zwischen der Frequenz f n und der Amplitude r n zeigt . Ebenso ergibt sich ein Phasenspektrum, das die Beziehung zwischen der Frequenz f n und der Phase f n zeigt . Der ursprüngliche Zeitverlauf kann auch aus a n und b n wiederhergestellt werdenunter Verwendung von Gleichung 3-2. Wir sollten beachten, dass ein Spektrum nur eine Quantität der Größe ist (dh keine Phaseninformation < ϕ> hat) und daher Spektraldaten allein nicht die Wiederherstellung der ursprünglichen Wellenform ermöglichen. Unter seinen Funktionen bietet der FFT-Analysator eine Technik zum Suchen von Zeitwellenformen aus Fourier-Transformationsdaten (dh eine inverse Fourier-Transformation). Um diese Funktion auszuführen, ist es notwendig, zuvor ein Fourier-Spektrum mit Phaseninformation (bestehend aus einem Realteil und einem Imaginärteil) zu speichern. Wenn Originalwellenformen gespeichert sind, kann der Analysator außerdem auch wieder eine FFT aus diesen Daten durchführen.
* Die Begriffe „Realteil“ und „Imaginärteil“ werden im folgenden Abschnitt erklärt.
3.2 Darstellung der Fourier-Reihe durch komplexe Exponentialfunktion
Ein FFT-Analysator zeigt die Ausdrücke "Realteil" und "Imaginärteil" an, wenn er Fourier-Spektren und Übertragungsfunktionen unter den verschiedenen Typen von Funktionen anzeigt, die er berechnet und verarbeitet. Diese Ausdrücke erscheinen, wenn eine Fourier-Reihe durch eine komplexe Ebene (Gauß-Ebene) dargestellt wird, und werden in einer Technik zur funktionalen Darstellung verwendet. Jeder Teil hat eine wichtige Bedeutung. In diesem Abschnitt werden wir versuchen, eine Fourier-Reihe in eine Angabe einer komplexen Exponentialfunktion zu transformieren, indem wir die Euler-Formel verwenden, und werden auf diese Weise die Begriffe "Realteil" und "Imaginärteil" erklären.
Die Erklärung unten mag etwas schwer zu verstehen sein, aber beginnen wir damit, uns ein Verständnis von Abbildung 3-3 unten zu verschaffen. Hier gehen wir nicht näher auf die komplexe Zahl und den Exponenten ein; wer mehr darüber wissen möchte, sei auf die einschlägige Fachliteratur verwiesen.
Eulers Formel lautet:

Gleichung 3.5
In der oben angegebenen Euler-Formel werden π, e und j wie folgt verstanden:
π: Pi, 3141592
e: Basis des Napierschen Logarithmus, e = 2,71828.... e t ist "e t ", ob differenziert oder integriert. d/dt (e t ) = e t
j : Wert, wobei j 2 = –1.
Wie Sie wissen, bestehen Zahlen aus reellen und imaginären Zahlen. Zahlen ohne aj-Wert heißen reelle Zahlen, solche mit aj-Wert heißen imaginäre Zahlen. Die komplexe Zahl Z = 1+1j auf einer komplexen Ebene (Gauß-Ebene) wird wie in Abbildung 3-2(a) dargestellt ausgedrückt. Unterdessen repräsentiert X = e jn ωt einen Kreis mit Radius = 1 auf einer komplexen Ebene, wie in Abbildung 3-2(b) gezeigt, wobei sich der Kreis gegen den Uhrzeigersinn (dh in positiver Richtung) mit einer Winkelgeschwindigkeit von n ![]() pro Sekunde dreht. Das bedeutet, dass die beiden Gleichungen Kosinus und Sinus, die den Ort einer Kugel in den Gleichungen 2-7 und 2-8 (aus dem vorherigen Bericht) darstellten, hier durch eine einzige Gleichung dargestellt werden. In ähnlicher Weise gilt Y = e - jn ωt- zeigt eine Drehung im Uhrzeigersinn (negativ) an. X und Y beziehen sich symmetrisch bezüglich der Achse der reellen Zahlen (Re-Achse) aufeinander, wobei Y eine konjugiert komplexe Zahl von X und X eine konjugiert komplexe Zahl von Y genannt wird. Konjugiert komplexe Zahlen werden mit einem "*" gekennzeichnet. ", zB Z * .
pro Sekunde dreht. Das bedeutet, dass die beiden Gleichungen Kosinus und Sinus, die den Ort einer Kugel in den Gleichungen 2-7 und 2-8 (aus dem vorherigen Bericht) darstellten, hier durch eine einzige Gleichung dargestellt werden. In ähnlicher Weise gilt Y = e - jn ωt- zeigt eine Drehung im Uhrzeigersinn (negativ) an. X und Y beziehen sich symmetrisch bezüglich der Achse der reellen Zahlen (Re-Achse) aufeinander, wobei Y eine konjugiert komplexe Zahl von X und X eine konjugiert komplexe Zahl von Y genannt wird. Konjugiert komplexe Zahlen werden mit einem "*" gekennzeichnet. ", zB Z * .

Abbildung 3.2
Wir ordnen die obige Gleichung 3.5 neu an, indem wir sie wie folgt in die Fourier-Reihen-Gleichungen 3.2 und 3.3 einsetzen:
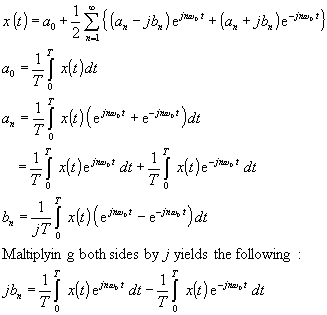
Gleichung 3.6
Die Multiplikation beider Seiten mit j ergibt Folgendes:


Gleichung 3.7, 3.7a, 3.7b, 3.7c
Betrachtet man den Fall, in dem n = 0 in Gleichung 3-7b oben angenommen wird, stimmt die rechte Seite von Gleichung 3.7b mit der von Gleichung 3.7a überein, weil e 0 = 1. Daher kann Gleichung 3-7 wie folgt umgeschrieben werden, unter der Annahme, dass n n = 0 zu nimmt ∞:.

Gleichung 3.8
Wenn wir außerdem davon ausgehen, dass n in Gleichung 3.7c n = –1 bis – annimmt ![]() , stimmt es mit der rechten Seite (n = 1 bis
, stimmt es mit der rechten Seite (n = 1 bis ![]() ) von Gleichung 3-7b überein. Daher kann X n * als eines behandelt werden, das existiert, wenn n von X n n = –1 bis – ist ∞. Dementsprechend können die Gleichungen 3-7, 7a, 7b und 7c, um das Obige zusammenzufassen, in einer sehr klaren Form wie folgt dargestellt werden:
) von Gleichung 3-7b überein. Daher kann X n * als eines behandelt werden, das existiert, wenn n von X n n = –1 bis – ist ∞. Dementsprechend können die Gleichungen 3-7, 7a, 7b und 7c, um das Obige zusammenzufassen, in einer sehr klaren Form wie folgt dargestellt werden:

Gleichung 3.9a, 3.9b
Gleichung 3-9a oben wird als Fourier-Reihe einer komplexen exponentiellen Anzeige bezeichnet und Gleichung 3-9b wird als Fourier-Entwicklung einer komplexen exponentiellen Anzeige bezeichnet. Da e jn ω0t und e -jn ω0t in Eulers Formel aus Kosinus und Sinus bestehen, ersetzt diese Formulierung die bisher gesehene Periodizität von Kosinus und Sinus und hat gleichzeitig die Natur eines Exponenten. Wenn wir e jn ω0t und e -jn ω0t ersetzen B. mit Sinus bzw. Cosinus und Gleichung 3-9b durch Cosinus ersetzen, entspricht dies der Gleichung für an in Gleichung 3-3. Wenn wir außerdem bedenken, dass der Kosinusterm und der Sinusterm eines Fourier-Koeffizienten der Realteil und der Imaginärteil einer komplexen Zahlenangabe sind, wird es angesichts der unten gezeigten Beziehung einfacher, die Beziehung zwischen den Fourier-Reihen zu verstehen und seine komplexe Zahlenangabe. (Um dies zu sehen, vergleichen Sie Abbildung 3-1 und Abbildung 3-3 miteinander.)

Nun wird die k-te Harmonische in diesem Zustand wie folgt dargestellt:

Abbildung 3.3
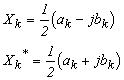
Gleichung 3.10
X k * ist eine konjugiert komplexe Zahl von X k . Wenn das Obige durch komplexe Koordinaten dargestellt wird, wobei der Realteil (Re) auf der x-Achse und der Imaginärteil (Im) auf der y-Achse aufgetragen sind, erscheinen X k * und X k bezüglich Re symmetrisch zueinander -Achse, wie in Abbildung 3-3 gezeigt. Da Abbildung 3-3 genauso betrachtet werden kann wie Abbildung 2-9 in Abschnitt 2-6 des vorherigen Berichts, kann die folgende Gleichung 3-11 aufgestellt werden:

Gleichung 3.11
X k wird hier Fourier-Spektrum genannt, 1/2a k der Realteil (Re) des Fourier-Spektrums und 1/2b k der Imaginärteil des Fourier-Spektrums (Im). Außerdem ist |X k | 2 wird als Leistungsspektrum bezeichnet. Übrigens zeigt das Fourier-Spektrum in einem FFT-Analysator ak und b k und das Leistungsspektrum zeigt 4|X k | 2 . Dies liegt daran, dass es bequem ist, diese Terme mit den in Abbildung 3-1 verwendeten r n , a n und b n darzustellen.
3.3 Fourier-Transformation
Da Gleichung 3-9a eine Fourier-Reihe ist, repräsentiert sie eine kontinuierliche, periodische, zeitabhängige Wellenform. Das Einsetzen von Gleichung 3-9b in diese Gleichung ergibt die nachstehende Gleichung 3-12. (Zur Vereinfachung der Berechnung wurde der Abschnitt 0 bis T der Wellenform durch -2/T bis 2/T ersetzt.) '

Gleichung 3.12
Betrachten wir hier die Verlängerung der Periode T auf – ∞ bis + ∞, so dass auch Wellenformen ohne Periodizität gehandhabt werden können. Wenn wir in Gleichung 3-12 für df eine sehr kleine Frequenz annehmen, die schließlich durch Vergrößern von T in 1/T erreicht wird, haben wir:

Gleichung 3.13
Wenn wir X(f) für den Teil in {} in der obigen Gleichung einsetzen, erhalten wir die folgenden Gleichungen:

Gleichung 3.14, 3.15
Gleichung 3-14 repräsentiert eine Fourier-Transformation und Gleichung 3-15 eine inverse Fourier-Transformation. Obwohl 1/T in Gleichung 3-14, der Fourier-Transformation, verschwindet, kann davon ausgegangen werden, dass es sich auf die inverse Transformationsseite von Gleichung 3-15 bewegt hat. Auf diese Weise kann verstanden werden, dass das Paar aus Fourier-Transformation und inverser Transformation dem Paar aus Fourier-Entwicklung und -Reihe entspricht, das in den obigen Gleichungen 3–9 behandelt wird. Achten Sie jedoch darauf, die Gleichungen 3-14 und 3-15 nicht miteinander zu verwechseln, da die beiden sehr ähnlich sind.
X(f) repräsentiert den Frequenzbereich und x(t) den Zeitbereich
Während bei der Fourier-Reihe das Spektrum in Form von unstetigen Harmonischen dargestellt wurde, erscheint es bei der Fourier-Transformation als Spektrum kontinuierlicher Frequenz, bei der die Periodizität unendlich erweitert wird, wodurch die Grundfrequenz f 0 (=1/T) annimmt auf einem sehr kleinen Wert.
Betrachten wir nun die Fourier-Transformation von x(t)=1.
Wir schneiden einen bestimmten Zeitabschnitt T aus einem unendlich fortlaufenden Wert von 1 heraus und betrachten den Rest als Null (0).
Lassen Sie uns versuchen, eine Fourier-Transformation unter dieser Annahme durchzuführen.
Abbildung 3-4 veranschaulicht zwei Fälle, T = 1 und T = 5. Die Vermutung ist in Abbildung 3-4a dargestellt, unterscheidet sich jedoch wesentlich von Abbildung 3-4b. Wenn T jedoch größer gemacht wird, wird die Wellenform schmaler und der Amplitudenwert nimmt ebenfalls zu, wodurch eine Wellenform erzeugt wird, die der in Abbildung 3-4a näher kommt. Dieser Unterschied entsteht, weil wir den unsichtbaren Anteil einfach als 0 angenommen haben und ein größeres T die Charakteristik der gesamten Wellenform natürlich deutlicher zeigt. Wie sich entnehmen lässt, wird die Frequenzauflösung (= 1/T) höher, wenn wir eine längere Zeit T wählen, für die eine Wellenform ausgeschnitten wird (als "Zeitauflösung" bezeichnet), was es uns ermöglicht, mehr zu sehen detailliertes Spektrum. Wenn umgekehrt die Zeit, für die eine Wellenform abgeschnitten wird, kurz eingestellt ist (dh die Zeitbasisauflösung ist hoch), die Frequenzauflösung wird grob und zeigt nur auf breiter Basis ein Spektrum an. Auf diese Weise besitzt die Fourier-Transformation eine so genannte natürliche Unsicherheit zwischen Zeitauflösung und Frequenzauflösung. Der FFT-Analysator ermöglicht es, diese Zeitdauer T als Datenlänge (Anzahl von Abtastungen) entsprechend der beabsichtigten Anwendung zu modifizieren.

Abbildung 3.4
3.4 Diskrete Fourier-Transformation
FFT-Analysator behandelt eine Zeitwellenform x(t) als diskontinuierliche Daten (diskrete Daten), die im Abtastintervall h erfasst werden.
Wenn die Abtastwertsequenz einer Anzahl N endlicher Datenpunkte, die im Abtastintervall h abgetastet werden, durch x(n) (n = 0, ... N-1) dargestellt wird, gilt die Fourier-Transformation gleichermaßen für diese Daten. Da die Multiplikation einer Zeitwellenform x(n) mit einer gegebenen Wellenform e -j2pft und die Integration einer Periode davon die Amplitude der Wellenform liefert, wenden wir diese diskreten Daten auf die Formel an, indem wir Gleichung 3.9b als Richtlinie verwenden:

Aus dem Obigen wird die Fourier-Transformationsformel der k-ten Harmonischen wie folgt ausgedrückt:

Gleichung 3.16
Gleichung 3.16 wird als diskrete Fourier-Transformation (DFT) bezeichnet. Darüber hinaus gilt die Beziehung von Gleichung 3.11 auch für diese Gleichung in der gleichen Weise wie für Gleichung 3.7b. In ähnlicher Weise wird die inverse diskrete Fourier-Transformation (IDFT) ausgedrückt durch:

Gleichung 3.17
Bitte beziehen Sie sich auf Abbildung 3.5 wo wir eine konzeptionelle Darstellung von Gleichung 3.16 zu Ihrer Information gegeben haben.

Abbildung 3.5
4. Abtasttheorem
Inwieweit können wir also ein harmonisches k berechnen?
Um eine ursprüngliche Wellenform zu kennen, ist es notwendig, die Abtastung mit einer Frequenz durchzuführen, die mindestens doppelt so hoch ist wie die der Wellenform. Dies wird als Abtasttheorem bezeichnet.
Betrachten wir nun den Fall, in dem eine Anzahl N von Abtastwerten für eine Wellenform mit der Periode T genommen wird. In diesem Fall werden das Abtastintervall h und seine Frequenz f s ausgedrückt durch:

Gleichung 3.18
Daher ist die Frequenz f m , die mit dem Abtasttheorem analysiert werden kann:

Gleichung 3.19
Die Analyse kann nämlich bis zur N/2-ten Harmonischen durchgeführt werden.
Wenn wir eine Wellenform mit Bandbegrenzung von 0 bis fm bei fs abtasten und eine DFT-Berechnung durchführen, erhalten wir ein Frequenzspektrum von - ∞ bis +∞. Abbildung 3-6 zeigt ein typisches Frequenzspektrum von -fm bis 4fm .
Wie in der obigen Abbildung zu sehen ist, hat das erhaltene Spektrum wiederholt denselben Wert, genau wie ein Papier, das bei ganzzahligen Vielfachen von f m gefaltet wird . Ein ähnliches Ergebnis wie in Abbildung 3-6 wird auch erhalten, wenn wir eine Wellenform mit einem von f m auf 2 f m begrenzten Band bei derselben Frequenz f s abtasten und dann die DFT-Berechnung durchführen. Diese Berechnung liefert uns jedoch die Komponenten des Bereichs 0 bis f in Wirklichkeit nicht existieren. Dies wird als "Aliasing"-Phänomen (oder "Faltungsfrequenz") bezeichnet, und eine Frequenz fm in diesem Zustand wird als Nyquist-Frequenz bezeichnet. Ein einfacher Blick auf nur die 0 bis f mBereich des erhaltenen Spektrums können Sie nicht feststellen, ob die ursprüngliche Wellenform von 0 bis f m oder von f m bis 2 f m reicht . Aus diesem Grund leitet ein FFT-Analysator Signale durch einen Tiefpassfilter (als "Aliasing-Filter" bezeichnet), der sie zuvor auf f m begrenzt und somit nur Signale unterhalb von f m definiert , um das Abtasttheorem zu erfüllen. Da außerdem Frequenzen bis zu f m plus a berücksichtigt werden müssen, um Frequenzen zu erhalten, die durch das Tiefpassfilter vollständig gedämpft werden können, ist ein FFT-Analysator so ausgelegt, dass er Spektren bis zu 1/1,28 von f m anzeigt nur (Abbildung 3.7).

|
Angenommen, der Frequenzbereich der FFT ist beispielsweise auf 1 kHz eingestellt, der FFT-Analysator tastet bei der Frequenz fs = 2,56 kHz ab, was dem 2,56-fachen des Frequenzbereichs entspricht.
|
Abbildung 3.7
Bitte beachten Sie, dass Abbildung 3.8 das Sampling-Theorem unter dem Gesichtspunkt von Zeitwellenformen untersucht, und Abbildungen 3.9a und 3.9b die Wellenformen zeigen, die von einem FFT-Analysator angezeigt werden, wenn der Aliasing-Filter eingeschaltet ist und aus.

| Abtastpunkt -- : An Abtastpunkten reproduzierte Wellenform Wenn das Originalsignal eine Frequenz kleiner als 1/2 (= f m ) der Abtastfrequenz f s hat, kann es wie in (a) gezeigt reproduziert werden, aber wenn die Frequenz größer ist, kann das ursprüngliche Signal nicht reproduziert werden und stattdessen findet eine Frequenzverstümmelung statt, wie die durch die gepunktete Linie in (b) angezeigte Wellenform. Wenn das Originalsignal eine Frequenz hat, die mit der Abtastfrequenz f m übereinstimmt , erscheint eine gerade Wellenform wie die gepunktete Linie in (c). |
Abbildung 3.8
| Durch die Verwendung des Anti-Aliasing-Filters tritt kein Aliasing auf. Die Zeitachsen-Wellenform erscheint jedoch nicht als vollständige Rechteckwelle, da das Filter keine Hochfrequenzkomponenten durchlässt und somit die Wellenform verzerrt. |
Abbildung 3.9a

| Ohne einen Anti-Aliasing-Filter scheint die Zeitachsen-Wellenform die ursprüngliche Rechteckwelle zu sein. Aliasing erscheint jedoch bei einem Ergebnis der FFT-Verarbeitung, das Frequenzkomponenten zeigt, die tatsächlich nicht existieren. |
Abbildung 3.9b
Diese Diskussion hat einen recht komplexen und mathematischen Ton angenommen. Wir hoffen, dass es Ihnen bis zu diesem Punkt klar war. An dieser Stelle möchten wir die Fourier-Reihe, die Fourier-Transformation, die DFT und das Sampling aus der Sicht eines FFT-Analysators mit einigen eingemischten Bildkonzepten besprechen. Ein Teil dieser Erklärung wird Zitate aus dem Buch „Introduction to Digital Signal“ enthalten Processing", geschrieben von Ken'ichi Kido.
Beginnen wir mit der Bezugnahme auf Abbildung 3.10. Wellenform "A" ist eine Zeitwellenform, die unendlich wiederholt wird, wobei ein Band auf weniger als eine Nyquist-Frequenz fm begrenzt ist. "B" ist das von "A" erhaltene Frequenzspektrum, das von seinem Ursprung über ± fm verteilt ist , und der Teil außerhalb dieses Bereichs ist Null (0). Unter der Annahme, dass das Spektrum X(f) von „B“ unendlich auf der Frequenzachse mit der Periode 2f x angeordnet ist , sind die unten angegebenen Fälle wahrscheinlich:

| Wenn f x = f m , Spektralwellenform von "C". Wenn f x < f m , Spektralwellenform von "D". Wenn f x > f m , Spektralwellenform von "E". |
Abbildung 3.10
Hier stellt die Spektralwellenform von "E" den Zustand dar, in dem die verschiedenen Spektren einander überlappen, wodurch bewirkt wird, dass Aliasing stattfindet. Die Spektralwellenformen von "C" und "D" sind identisch mit dem Spektrum X(f) von x(t) im Bereich von -fm bis + fm . Um den Betrachtungswinkel zu ändern, betrachten wir nun den Abtastzug x n , wobei x(t) bei 2f x abgetastet wird . Spektrum x n in diesem Zustand ist:

Gleichung 3.20
Dies stellt "C", "D" und "E" mit einer Gleichung dar. Mit anderen Worten, wenn wir eine kontinuierliche Wellenform x(t) mit auf f x begrenztem Band bei der Abtastfrequenz 2f x abtasten , suchen wir das Spektrum X(f) aus den Daten seiner unendlichen Abtastfolge {x n } und betrachten seine Frequenz Bereich von –f x bis +f x , dann stellen wir fest, dass es sich um ein eigenständiges Frequenzspektrum X(f) von x(t) handelt ("C", "D").
Da die Anwendung der inversen Fourier-Transformation auf X(f) x(t) ergibt, ist die Abtastwertsequenz bei jedem 1/(2f x) hat genügend Informationen, um eine kontinuierliche Wellenform x(t) anzuzeigen. Wenn die ursprüngliche Wellenform eine Frequenz hat, die höher als die Abtastfrequenz ist, erscheinen aufgrund des Aliasing-Effekts überlappende Spektren (wie die in „E“ gezeigten), und das resultierende Spektrum unterscheidet sich von X(f), wodurch es entsteht es ist daher unmöglich, x(t) zu reproduzieren.
Die Diskussion bis zu diesem Punkt hat sich auf die Fourier-Transformation konzentriert.
Nehmen wir als nächstes an, dass die Wellenform von "A" unendlich mit einer Periode T wie "F" wiederholt wird, so dass sich das aus der Fourier-Entwicklung dieser Wellenform resultierende Frequenzspektrum als lineares Spektrum darstellt, das auf der Frequenzachse im Intervall 1/T angeordnet ist . Da diese Wellenform ihre Frequenzkomponente auf weniger als fx begrenzt hat, erscheint das Spektrum wie „G“, und die Hüllkurve dieses linearen Spektrums stimmt mit dem kontinuierlichen Spektrum von „B“ überein. Wenn wir hier davon ausgehen, dass das Spektrum von „G“ identisch mit einem Spektrum „H“ ist, das sich unendlich mit der Periode 2fx wiederholt, wie „C“ und „D“, dann ist die Zeitwellenform, die durch Anwendung einer inversen Fourier-Transformation auf „H“ erhalten wird. erscheint als Abtastwertfolge, die sich unendlich mit der Periode T wiederholt, wie in "I" gezeigt. Das heißt, sowohl die Zeitwellenform als auch das Spektrum erscheinen als periodisch und unendlich wiederholte Abtastwertfolge. Diese Beziehungen werden durch DFT und IDFT der Gleichungen 3-16 und 3-17 dargestellt. Da die folgenden Teile der Gleichungen 3-16 und 3-17 periodische Funktionen sind, die mit einer bestimmten Periode wiederholt dieselben Werte annehmen,

Darüber hinaus ist auch klar, dass sie dem Benutzer ausreichende Informationen geben, vorausgesetzt, dass die Spektren von 0 bis fx korrekt erhalten werden können. Unten ist zu Referenzzwecken eine Gleichung zur Wiederherstellung einer kontinuierlichen Wellenform aus einem Spektrum angegeben.
Musterzug {x n } wird ausgedrückt durch:

Gleichung 3.21
Und der Fourier-Koeffizient im Term von –n seines Spektrums X(f) entspricht x n . Außerdem lässt sich aus der Abtastwertfolge {x n } durch folgende Gleichung (siehe Abbildung 3-11) ein kontinuierlicher Originalsignalverlauf x(t) gewinnen:

Gleichung 3.22

Abbildung 3.11
Lassen Sie uns diese Erklärung von Fourier-Reihen und Fourier-Transformationen vorerst abschließen, indem wir eine kurze Zusammenfassung von Informationen über DFTs geben.
Zusammenfassung
Angenommen, das Band des mit der Periode T unendlich wiederholten Signals x(t) ist auf unterhalb einer bestimmten Frequenz begrenzt, und es kann ein diskretes Spektrum (lineares Spektrum) X(f) gefunden werden, das DFT bei jedem 1/T = 1/Nh durchführt , basierend auf einem diskreten Abtastwertzug {x n }, der aus Signalen der Periode T in einer Anzahl N in einem konstanten Intervall h gemäß dem Abtasttheorem erhalten wird. Ebenso kann ein diskreter Probenzug {x n } reproduziert werden, indem eine IDFT durchgeführt wird. Ein FFT-Analysator zeigt eine Probenfolge von 0 bis N-1 Proben als Zeitsignal im Zeitbereich und ein Frequenzspektrum (lineares Spektrum) von 0 bis f m /1,28 im Frequenzbereich.


